Question 1. Find the equation of the tangent to the curve √x + √y = a at the point (a2/4, a2/4).
Solution:
We have,
√x + √y = a
On differentiating both sides w.r.t. x, we get
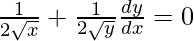
dy/dx = -√y/√x
Given, (x1, y1) = (a2/4, a2/4),
Slope of tangent, m = 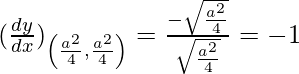
The equation of tangent is,
y – y1 = m (x – x1)
y – a2/4 = –1(x – a2/4)
y – a2/4 = –x + a2/4
x + y = a2/2
Question 2. Find the equation of the normal to y = 2x3 − x2 + 3 at (1, 4).
Solution:
We have,
y = 2x3 − x2 + 3
On differentiating both sides w.r.t. x, we get
dy/dx = 6x2 – 2x
Slope of tangent = 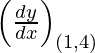 = 6 (1)2 – 2 (1) = 4
= 6 (1)2 – 2 (1) = 4
Slope of normal = – 1/Slope of tangent = – 1/4
Given, (x1, y1) = (1, 4),
The equation of normal is,
y – y1 = m (x – x1)
y – 4 = -1/4 (x – 1)
4y – 16 = – x + 1
x + 4y = 17
Question 3. Find the equation of the tangent and the normal to the following curve at the indicated point:
(i) y = x4 − bx3 + 13x2 − 10x + 5 at (0, 5)
Solution:
We have,
y = x4 − bx3 + 13x2 − 10x + 5
On differentiating both sides w.r.t. x, we get
dy/dx = 4x3 – 3bx2 + 26x – 10
Slope of tangent, m= 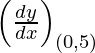 = -10
= -10
Given, (x1, y1) = (0, 5)
The equation of tangent is,
y – y1 = m (x – x1)
y – 5 = – 10 (x – 0)
y – 5 = -10x
y + 10x – 5 = 0
The equation of normal is,
y – y1 = -1/m (x – x1)
y – 5 = 1/10 (x – 0)
10y – 50 = x
x – 10y + 50 = 0
(ii) y = x4 − 6x3 + 13x2 − 10x + 5 at x = 1
Solution:
We have,
y = x4 − 6x3 + 13x2 − 10x + 5
When x = 1, we have y = 1 – 6 + 13 – 10 + 5 = 3
So, (x1, y1) = (1, 3)
Now, y = x4 − 6x3 + 13x2 − 10x + 5
On differentiating both sides w.r.t. x, we get
dy/dx = 4 x3 – 18 x2 + 26x – 10
Slope of tangent, m = 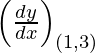 = 4 – 18 + 26 – 10 = 2
= 4 – 18 + 26 – 10 = 2
The equation of tangent is,
y – y1 = 2 (x – x1)
y – 3 = 2 (x – 1)
y – 3 = 2x – 2
2x – y + 1 = 0
The equation of normal is,
y – y1 = -1/m (x – x1)
y – 3 = -1/2 (x – 1)
2y – 6 = – x + 1
x + 2y – 7 = 0
(iii) y = x2 at (0, 0)
Solution:
We have,
y = x2
On differentiating both sides w.r.t. x, we get
dy/dx = 2x
Given, (x1, y1) = (0, 0)
Slope of tangent, m= 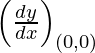 = 2 (0) = 0
= 2 (0) = 0
The equation of tangent is,
y – y1 = m (x – x1)
y – 0 = 0 (x – 0)
y = 0
The equation of normal is,
y – y1 = -1/m (x – x1)
y – 0 = -1/0 (x – 0)
x = 0
(iv) y = 2x2 − 3x − 1 at (1, −2)
Solution:
We have,
y = 2x2 − 3x − 1
On differentiating both sides w.r.t. x, we get
dy/dx = 4x – 3
Given, (x1, y1) = (1, -2)
Slope of tangent, m = 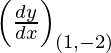 = 4 – 3 = 1
= 4 – 3 = 1
The equation of tangent is,
y – y1 = m (x – x1)
y + 2 = 1 (x – 1)
y + 2 = x – 1
x – y – 3 = 0
The equation of normal is,
y – y1 = -1/m (x – x1)
y + 2 = -1 (x – 1)
y + 2 = -x + 1
x + y + 1 = 0
(v) 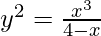 at (2, -2)
at (2, -2)
Solution:
We have,
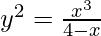
On differentiating both sides w.r.t. x, we get
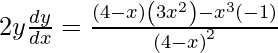
= 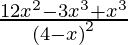
= 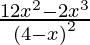
Given, (x1, y1) = (2, -2)
Slope of tangent, m= 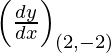 =
= 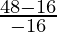 = -2
= -2
The equation of tangent is,
y – y1 = m (x – x1)
y + 2 = -2 (x – 2)
y + 2 = -2x + 4
2x + y – 2 = 0
The equation of normal is,
y – y1 = -1/m (x – x1)
y + 2 = 1/2 (x – 2)
2y + 4 = x – 2
x – 2y – 6 = 0
(vi) y = x2 + 4x + 1 at x = 3
Solution:
We have,
y = x2 + 4x + 1
On differentiating both sides w.r.t. x, we get,
dy/dx = 2x + 4
When x = 3, y = 9 + 12 + 1 = 22
So, (x1, y1) = (3, 22)
Slope of tangent, m= 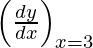 = 10
= 10
The equation of tangent is,
y – y1 = m (x – x1)
y – 22 = 10 (x – 3)
y – 22 = 10x – 30
10x – y – 8 = 0
The equation of normal is,
y – y1 = -1/m (x – x1)
y – 22 = -1/10 (x – 3)
10y – 220 = – x + 3
x + 10y – 223 = 0
(vii) 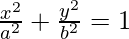 at (a cos θ, b sin θ)
at (a cos θ, b sin θ)
Solution:
We have,
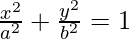
On differentiating both sides w.r.t. x, we get
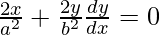
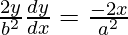
dy/dx = -x b2/y a2
Slope of tangent, m= 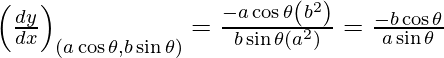
Given, (x1, y1) = (a cos θ, b sin θ)
The equation of tangent is,
y – y1 = m (x – x1)
y – b sin θ = -bcosθ/asinθ (x – a cos θ)
ay sin θ – ab sin2 θ = -bx cos θ + ab cos2 θ
bx cos θ + ay sin θ = ab
On dividing by ab, we get
x/a cosθ + y/b sinθ = 1
The equation of normal is,
y – y1 = -1/m (x – x1)
y – b sin θ = asinθ/bcosθ (x – a cos θ)
by cos θ – b2 sin θ cos θ = ax sin θ – a2 sin θ cos θ
ax sin θ – by cos θ = (a2 – b2) sin θ cos θ
On dividing by sin θ cos θ, we get
ax sec θ – by cosec θ = a2 – b2
(viii) 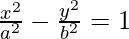 at (a sec θ, b tan θ)
at (a sec θ, b tan θ)
Solution:
We have,
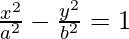
On differentiating both sides w.r.t. x, we get
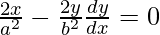
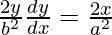
dy/dx = x b2/y a2
Slope of tangent}, m= 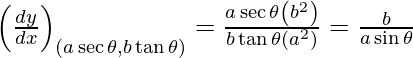
Given, (x1, y1) = (a sec θ, b tan θ)
The equation of tangent is,
y – y1 = m (x – x1)
y – b tan θ = 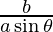 (x – a sec θ)
(x – a sec θ)
ay sin θ – ab(sin2 θ/cos θ) = bx – (ab/cos θ)
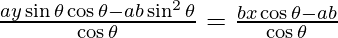
ay sin θ cos θ – ab sin2 θ = bx cos θ – ab
bx cos θ – ay sin θ cos θ = ab (1 – sin2 θ)
bx cos θ – ay sin θ cos θ = ab cos2 θ
On dividing by ab cos2 θ, we get
x/a sec θ – y/b tan θ = 1
The equation of normal is,
y – y1 = -1/m (x – x1)
y – b tan θ = -a sin θ/b (x – a sec θ)
by – b2 tan θ = -ax sin θ + a2 tan θ
ax sin θ + by = (a2 + b2) tan θ
On dividing by tan θ, we get
ax cos θ + by cot θ = a2 + b2
(ix) y2 = 4ax at (a/m2, 2a/m)
Solution:
We have,
y2 = 4ax
On differentiating both sides w.r.t. x, we get
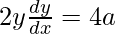
dy/dx = 2a/y
Given, (x1, y1) = (a/m2, 2a/m)
Slope of tangent = 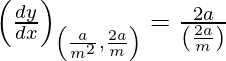 = m
= m
The equation of tangent is,
y – y1 = m (x – x1)
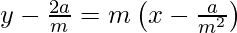
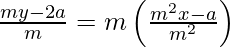
my – 2a = m2 x – a
m2 x – my + a = 0
The equation of normal is,
y – y1 = -1/m (x – x1)
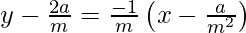
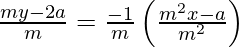
m3 y – 2a m2 = – m2 x + a
m2 x + m3 y – 2a m2 – a = 0
(x) c2 (x2 + y2) = x2y2 at (c/cos θ, c/sin θ)
Solution:
We have,
c2 (x2 + y2) = x2y2
On differentiating both sides w.r.t. x, we get
2x c2 + 2y c2(dy/dx) = x2 2y(dy/dx) + 2x y2
dy/dx(2y c2 – 2 x2 y) = 2x y2 – 2x c2
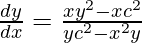
Slope of tangent, m= 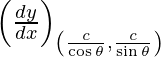
= 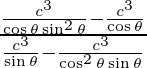
= 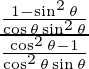
= 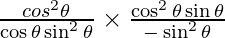
= -cos3 θ/ sin3 θ
Given, (x1, y1) = (c/cos θ, c/sin θ)
The equation of tangent is,
y – y1 = m (x – x1)
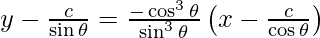
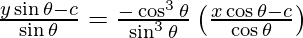
sin2 θ (y sin θ – c) = -cos2 θ (x cos θ – c)
y sin3 θ – c sin2 θ = – x cos3 θ + c cos2 θ
x cos3 θ + y sin3 θ = c ( sin2 θ + cos2 θ)
x cos3 θ + y sin3 θ = c
The equation of normal is,
y – y1 = -1/m (x – x1)
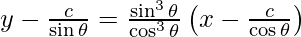
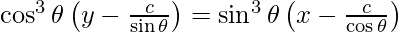
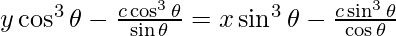
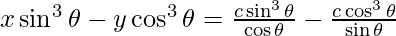
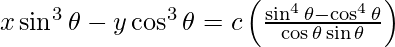
![Rendered by QuickLaTeX.com x \sin^3 \theta - y \cos^3 \theta = c\left[ \frac{\left( \sin^2 \theta + \cos^2 \theta \right)\left( \sin^2 \theta - \cos^2 \theta \right)}{\cos\theta \sin\theta} \right]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-e0be6ba0e0a40439800980bff7b09216_l3.png)
![Rendered by QuickLaTeX.com \sin^3 \theta - y \cos^3 \theta =2c \left[ \frac{- \left( \cos^2 \theta - \sin^2 \theta \right)}{2\cos\theta \sin\theta} \right]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-3a6ecbbacf92987bf95bf7652d1978d1_l3.png)
sin3 θ – ycos3 θ = 2c[-cos (2θ)/sin(2θ)]
sin3 θ – y cos3 θ = -2c cot 2θ
sin3 θ – y cos3 θ + 2c cot 2θ = 0
(xi) xy = c2 at (ct, c/t)
Solution:
We have,
xy = c2
On differentiating both sides w.r.t. x, we get
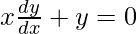
dy/dx = – y/x
Given, (x1, y1) = (ct, c/t)
Slope of tangent, m= 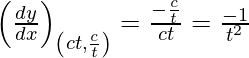
The equation of tangent is,
y – y1 = m (x – x1)
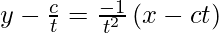
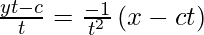
yt2 – ct = -x + ct
x + y t2 = 2ct
The equation of normal is,
y – y1 = -1/m (x – x1)
y – c/t – t2(x – ct)
yt – c = t3 x – c t4
x t3 – yt = c t4 – c
(xii) 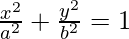 at (x1, y1)
at (x1, y1)
Solution:
We have,
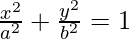
On differentiating both sides w.r.t. x,
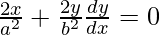
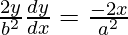
dy/dx = – x b2/y a2
Slope of tangent, m= 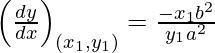
The equation of tangent is,
y – y1 = m (x – x1)
y – y1 = – x1 b2/y1 a2(x – x1)
y y1 a2 – y12 a2 = -x x1 b2 + x12 b2
x x1 b2 + y y1 a2 = x12 b2 + y12 a2 . . . . (1)
Given (x1, y1) lies on the curve, we get
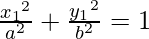
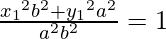
x12 b2 + y12 a2 = a2 b2
Substituting this in (1), we get
x x1 b2 + y y1 a2 = a2 b2
On dividing this by a2 b2, we get
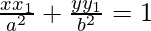
The equation of normal is,
y – y1 = m (x – x1)
y – y1 = y1 a2/x1 b2(x – x1)
y x1 b2 – x1 y1 b2 = x y1 a2 – x1 y1 a2
x y1 a2 – y x1 b2 = x1 y1 a2 – x1 y1 b2
x y1 a2 – y x1 b2 = x1 y1 (a2 – b2)
On dividing by x1 y1, we get
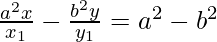
(xiii) 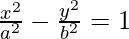 at (x0 , y0)
at (x0 , y0)
Solution:
We have,
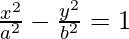
On differentiating both sides w.r.t. x, we get
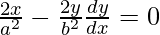
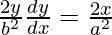
dy/dx = x b2/y a2
Slope of tangent, m= 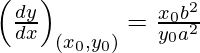
The equation of tangent is,
y – y1 = m (x – x1)
y – y0 = x0 b2/y0 a2(x – x0)
y y0 a2 – y02 a2 = x x0 b2 – x02 b2
x x0 b2 – y y0 a2 = x02 b2 – y02 a2 . . . . (1)
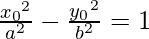
x02 b2 – y02 a2 = a2 b2
Substituting this in eq(1), we get,
x x0 b2 – y y0 a2 = a2 b2
Dividing this by a2 b2, we get
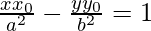
The equation of normal is,
y – y1 = m (x – x1)
y – y0 = y0 a2/x0 b2(x – x0)
y x0 b2 – x0 y0 b2 = -x y0 a2 + x0 y0 a2
x y0 a2 + y x0 b2 = x0 y0 a2 + x0 y0 b2
x y0 a2 + y x0 b2 = x0 y0 (a2 + b2)
Dividing by x0 y0, we get
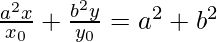
(xiv) 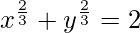 at (1, 1)
at (1, 1)
Solution:
We have,
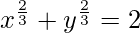
On differentiating both sides w.r.t. x, we get
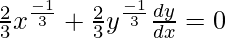
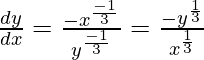
Slope of tangent, m= 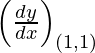 = -1
= -1
Given, (x1, y1) = (1, 1)
The equation of tangent is,
y – y1 = m (x – x1)
y – 1 = -1 (x – 1)
y – 1 = -x + 1
x + y – 2 = 0
The equation of normal is,
y – y1 = -1/m (x – x1)
y – 1 = 1 (x – 1)
y – 1 = x – 1
y – x = 0
(xv) x2 = 4y at (2, 1)
Solution:
We have,
x2 = 4y
On differentiating both sides w.r.t. x, we get
2x = 4dy/dx
dy/dx = x/2
Slope of tangent, m= 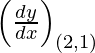 = 2/2 = 1
= 2/2 = 1
Given, (x1, y1) = (2, 1)
The equation of tangent is,
y – y1 = m (x – x1)
y – 1 = 1 (x – 2)
y – 1 = x – 2
x – y – 1 = 0
The equation of normal is,
y – y1 = -1/m (x – x1)
y – 1 = – 1 (x – 2)
y – 1 = – x + 2
x + y – 3 = 0
(xvi) y2 = 4x at (1, 2)
Solution:
We have,
y2 = 4x
On differentiating both sides w.r.t. x, we get
2y (dy/dx) = 4
dy/dx = 2/y
Slope of tangent, m= 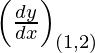 = 2/2 = 1
= 2/2 = 1
Given, (x1, y1) = (1, 2)
The equation of tangent is,
y – y1 = m (x – x1)
y – 2 = 1 (x – 1)
y – 2 = x – 1
x – y + 1 = 0
The equation of normal is,
y – y1 = -1/m (x – x1)
y – 2 = -1 (x – 1)
y – 2 = -x + 1
x + y – 3 = 0
(xvii) 4x2 + 9y2 = 36 at (3 cos θ, 2 sin θ)
Solution:
We have,
4x2 + 9y2 = 36
On differentiating both sides w.r.t. x, we get
8x + 18y dy/dx = 0
18y dy/dx = – 8x
dy/dx = -8x/18y = -4x/9y
Slope of tangent, m = 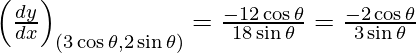
The equation of tangent is,
y – y1 = m (x – x1)
y – 2 sin θ = -2 cos θ/3 sin θ(x – 3 cos θ)
3y sin θ – 6 sin2 θ = -2x cos θ + 6 cos2 θ
2x cos θ + 3y sin θ = 6 (cos2 θ + sin2 θ)
2x cos θ + 3y sin θ = 6
The equation of normal is,
y – y1 = -1/m (x – x1)
y – 2 sin θ = -3 sin θ/2 cos θ(x – 3 cos θ)
2y cos θ – 4 sin θ cos θ = 3x sin θ – 9 sin θ cos θ
3x sin θ – 2y cos θ – 5sin θ cos θ = 0
(xviii) y2 = 4ax at (x1, y1)
Solution:
We have,
y2 = 4ax
On differentiating both sides w.r.t. x, we get
2y dy/dx = 4a
dy/dx = 2a/y
At (x1, y1), we have
Slope of tangent = 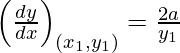 = m
= m
The equation of tangent is,
y – y1 = m (x – x1)
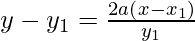
y y1 – y12 = 2ax – 2a x1
y y1 – 4a x1 = 2ax – 2a x1
y y1 = 2ax + 2a x1
y y1 = 2a (x + x1)
The equation of normal is,
y – y1 = -1/m (x – x1)
y – y1 = -y1/2a (x – x1)
(xix) 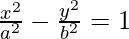 at (√2a, b)
at (√2a, b)
Solution:
We have,
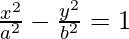
On differentiating both sides w.r.t. x, we get
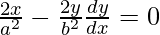
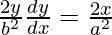
dy/dx = x b2/y a2
Slope of tangent, m= 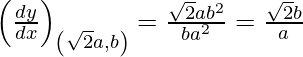
The equation of tangent is,
y – y1 = m (x – x1)
y – b = √2b/a(x – √2a)
ay – ab = √2 bx – 2ab
√2 bx – ay = ab
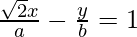
The equation of normal is,
y – y1 = -1/m (x – x1)
y – b = – a/√2b(x – √2a)
√2 by – √2 b2 = – ax + √2 a2
ax + √2 by = √2 b2 + √2 a2
ax/√2 + by = a2 + b2
Question 4. Find the equation of the tangent to the curve x = θ + sin θ, y = 1 + cos θ at θ = π/4.
Solution:
We have,
x = θ + sin θ, y = 1 + cos θ
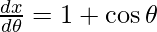 and
and 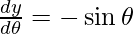
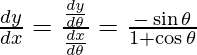
Slope of tangent, m = 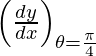
= 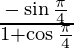
= 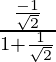
= 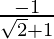
= 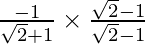
= 1 – √2
Given, (x1, y1) = (π/4 + sin π/4, 1 + cos π/4) = (π/4 + 1/√2, 1 + 1/√2)
The equation of tangent is,
y – y1 = m (x – x1)
y – (1 + 1/√2) = (1 – √2) [x – (π/4 + 1/√2)]
y – 1 – 1/√2 = (1 – √2) (x – π/4 – 1/√2)
Question 5. Find the equation of the tangent and the normal to the following curve at the indicated points.
(i) x = θ + sin θ, y = 1 + cos θ at θ = π/2
Solution:
We have,
x = θ + sin θ and y = 1 + cos θ
dx/dθ = 1 + cos θ and dy/dθ = -sinθ
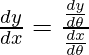
= 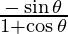
Slope of tangent, m= 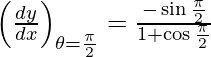
= -1/(1 + 0)
= -1
Given, (x1, y1) = (π/2 + sin π/2, 1 + cos π/2) = (π/2 + 1, 1)
The equation of tangent is,
y – y1 = m (x – x1)
y – 1 = -1 (x – π/2 – 1)
2y – 2 = – 2x + π + 2
x + 2y – π – 4 = 0
The equation of normal is,
y – y1 = -1/m (x – x1)
y – 1 = 1 (x – π/2 -1)
2y – 2 = 2x – π – 2
2x – 2y = π
(ii) 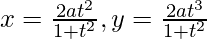 at t = 1/2
at t = 1/2
Solution:
We have,
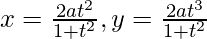
dx/dt = 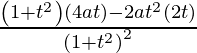
= 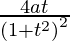
dy/dt = 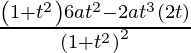
= 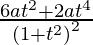
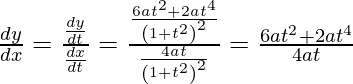
Slope of tangent, m= 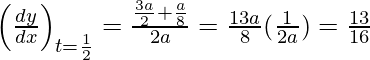
Given, (x1, y1) = 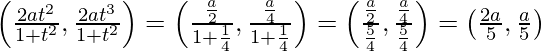
The equation of tangent is,
y – y1 = m (x – x1)
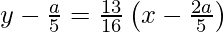
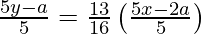
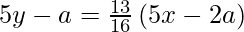
80y – 16a = 65x – 26a
65x – 80y – 10a = 0
13x – 16y – 2a = 0
The equation of normal is,
y – y1 = -1/m (x – x1)
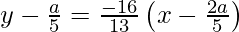
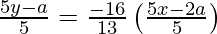
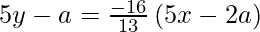
65y – 13a = – 80x + 32a
80x + 65y – 45a = 0
16x + 13y – 9a = 0
(iii) x = at2, y = 2at at t = 1
Solution:
We have,
x = at2, y = 2at
dx/dt = 2at and dy/dt = 2a
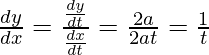
Slope of tangent, m= 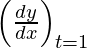 = 1
= 1
Given, (x1 , y1) = (a, 2a)
The equation of tangent is,
y – y1 = m (x – x1)
y – 2a = 1 (x – a)
y – 2a = x – a
x – y + a = 0
Equation of normal:
y – y1 = -1/m (x – x1)
y – 2a = – 1 (x – a)
y – 2a = – x + a
x + y = 3a
(iv) x = a sec t, y = b tan t at t
Solution:
We have,
x = a sec t, y = b tan t
dx/dt = a sect tant and dy/dt = b sec2t
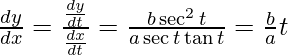
Slope of tangent, m = 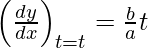
Given (x1, y1) = (a sec t, b tan t)
The equation of tangent is,
y – y1 = m (x – x1)
y – b tan t = (b/a) cosec t (x – a sec t)
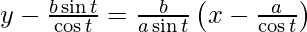
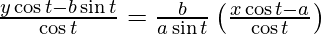
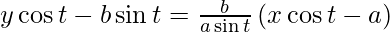
ay sin t cos t – ab sin2 t = bx cos t – ab
bx cos t – ay sin t cos t – ab (1 – sin2 t) = 0
bx cos t – ay sin t cos t = ab cos2 t
On dividing by cos2 t, we get
bx sec t – ay tan t = ab
The equation of normal is,
y – y1 = -1/m (x – x1)
y – b tant = -a/b sint(x – asect)
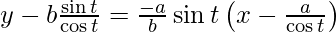
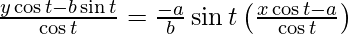
ycost − bsint = − a/bsint(xcost − a)
by cos t – b2 sin t = – ax sin t cos t + a2 sin t
ax sin t cos t + by cos t = (a2 + b2) sin t
On dividing both sides by sin t, we get
ax cos t + by cot t = a2 + b2
(v) x = a(θ + sin θ), y = a(1 − cos θ) at θ
Solution:
We have,
x = a(θ + sin θ), y = a(1 − cos θ)
dx/dθ = a(1 + cosθ) and dy/dθ = asinθ
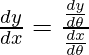
= 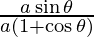
= 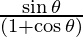
= 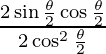
= tan θ/2 . . . . (1)
Slope of tangent, m= 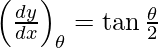
Given (x1, y1) = [a(θ + sin θ), a(1 − cos θ)]
The equation of tangent is,
y – y1 = m (x – x1)
y – a (1 – cos θ) = tan θ/2 [x – a (θ + sin θ)]
y − a(2sin2θ/2) = xtanθ/2 − aθtanθ/2 − atanθ/2sinθ
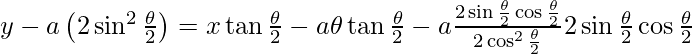
y − 2asin2θ/2 =(x − aθ)tan θ/2 − 2asin2θ/2
y = (x – aθ) tan θ/2
The equation of normal is,
y – a (1 – cos θ) = -cot θ/2 [x – a (θ + sin θ)]
tanθ/2[y − a(2sin2θ/2)] = −x + aθ + asinθ
tanθ/2[y − a{2(1 − cos2θ/2)}] = −x + aθ + asinθ
tan θ/2 (y – 2a) + a (2sin θ/2 cosθ/2 = -x + aθ + a sinθ
tan θ/2 (y – 2a) + a sin θ = -x + aθ + a sin θ
tan θ/2 (y – 2a) = – x + aθ
tan θ/2 (y – 2a) + x – θ = 0
(vi) x = 3 cos θ − cos3 θ, y = 3 sin θ − sin3 θ
Solution:
We have,
x = 3 cos θ − cos3 θ, y = 3 sin θ − sin3 θ
dx/dθ = -3sin θ + 3 cos2θ sin θ and dy/dθ = 3 cos θ – 3 sin2θ cos θ
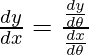
= 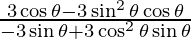
= 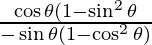
= cos3 θ/ -sin3 θ
= tan3 θ
So the equation of the tangent at θ is,
y – 3 sin θ + sin3 θ = -tan3 θ (x – 3 cos θ + cos3 θ)
4 (y cos3 θ – x sin3 θ) = 3 sin 4θ
So the equation of normal at θ is,
y – 3 sin θ + sin3 θ= (1/tan3 θ) (x – 3 cos θ + cos3 θ)
sin3 θ – x cos3 θ = 3sin4 θ – sin6 θ – 3cos4 θ + cos6 θ
Question 6. Find the equation of the normal to the curve x2 + 2y2 − 4x − 6y + 8 = 0 at the point whose abscissa is 2?
Solution:
Given that abscissa = 2. i.e., x = 2
x2 + 2y2 − 4x − 6y + 8 = 0 . . . . (1)
On differentiating both sides w.r.t. x, we get
2x + 4y dy/dx – 4 – 6 dy/dx = 0
dy/dx(4y – 6) = 4 – 2x
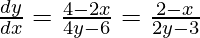
When x = 2, we get
4 + 2y2 – 8 – 6y + 8 = 0
2y2 – 6y + 4 = 0
y2 – 3y + 2 = 0
y = 2 or y = 1
m (tangent) at x = 2 is 0
Normal is perpendicular to tangent so, m1m2 = –1
m (normal) at x = 2 is 1/0, which is undefined.
The equation of normal is given by y – y1 = m (normal) (x – x1)
x = 2
Like Article
Suggest improvement
Share your thoughts in the comments
Please Login to comment...