Class 12 RD Sharma Solutions – Chapter 11 Differentiation – Exercise 11.5 | Set 1
Last Updated :
26 May, 2021
Question 1. Differentiate y = x1/x with respect to x.
Solution:
We have,
=> y = x1/x
On taking log of both the sides, we get,
=> log y = log x1/x
=> log y = (1/x) (log x)
On differentiating both sides with respect to x, we get,
=> 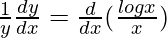
=> 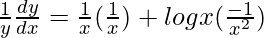
=> 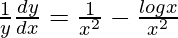
=> 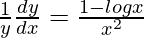
=> 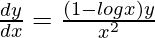
=> 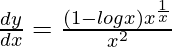
Question 2. Differentiate y = xsin x with respect to x.
Solution:
We have,
=> y = xsin x
On taking log of both the sides, we get,
=> log y = log xsin x
=> log y = sin x log x
On differentiating both sides with respect to x, we get,
=> 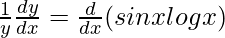
=> 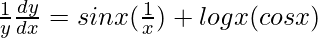
=> 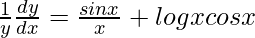
=> ![Rendered by QuickLaTeX.com \frac{dy}{dx}=y\left[\frac{sinx}{x}+logxcosx\right]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-78830849d8b08964e83eeef89d7e7240_l3.png)
=> ![Rendered by QuickLaTeX.com \frac{dy}{dx}=x^{sinx}\left[\frac{sinx}{x}+logxcosx\right]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-b4d8d934efc2c944d7dbcd9a8fed122f_l3.png)
Question 3. Differentiate y = (1 + cos x)x with respect to x.
Solution:
We have,
=> y = (1 + cos x)x
On taking log of both the sides, we get,
=> log y = log (1 + cos x)x
=> log y = x log (1 + cos x)
On differentiating both sides with respect to x, we get,
=> ![Rendered by QuickLaTeX.com \frac{1}{y}\frac{dy}{dx}=\frac{d}{dx}[x log (1 + cos x)]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-43f779a8ee3c0ffa3c4e9021f815017d_l3.png)
=> 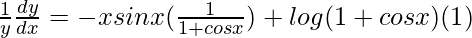
=> 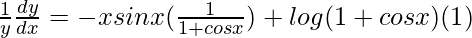
=> 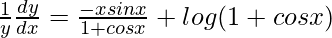
=> ![Rendered by QuickLaTeX.com \frac{dy}{dx}=y\left[log(1+cosx)-\frac{xsinx}{1+cosx}\right]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-5c4b2fb21986702702287fb095574865_l3.png)
=> ![Rendered by QuickLaTeX.com \frac{dy}{dx}=(1+cos x)^x\left[log(1+cosx)-\frac{xsinx}{1+cosx}\right]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-2655026710c2b2aba99b750185cf95f4_l3.png)
Question 4. Differentiate 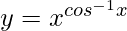 with respect to x.
with respect to x.
Solution:
We have,
=> 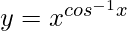
On taking log of both the sides, we get,
=> log y = log 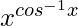
=> log y = cos−1 x log x
On differentiating both sides with respect to x, we get,
=> 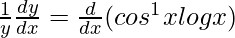
=> 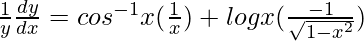
=> 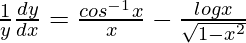
=> ![Rendered by QuickLaTeX.com \frac{dy}{dx}=y\left[\frac{cos^{-1}x}{x}-\frac{logx}{\sqrt{1-x^2}}\right]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-9ee9f4bb4f0895608bdb86a5538e9bea_l3.png)
=> ![Rendered by QuickLaTeX.com \frac{dy}{dx}=x^{cos^{-1}x}\left[\frac{cos^{-1}x}{x}-\frac{logx}{\sqrt{1-x^2}}\right]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-553358dc27cb45309d2af2d2a919231e_l3.png)
Question 5. Differentiate y = (log x)x with respect to x.
Solution:
We have,
=> y = (log x)x
On taking log of both the sides, we get,
=> log y = log (log x)x
=> log y = x log (log x)
On differentiating both sides with respect to x, we get,
=> ![Rendered by QuickLaTeX.com \frac{1}{y}\frac{dy}{dx}=\frac{d}{dx}[x log (log x)]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-03e254de2e177f82a87ae6bda74a75f1_l3.png)
=> 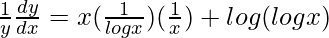
=> 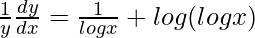
=> ![Rendered by QuickLaTeX.com \frac{dy}{dx}=y\left[\frac{1}{logx}+log(logx)\right]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-8416217167070e1f830b894e41eb761a_l3.png)
=> ![Rendered by QuickLaTeX.com \frac{dy}{dx}=(logx)^x\left[\frac{1}{logx}+log(logx)\right]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-df1a78f2454d865e74750b3619ff0be8_l3.png)
Question 6. Differentiate y = (log x)cos x with respect to x.
Solution:
We have,
=> y = (log x)cos x
On taking log of both the sides, we get,
=> log y = log (log x)cos x
=> log y = cos x log (log x)
On differentiating both sides with respect to x, we get,
=> ![Rendered by QuickLaTeX.com \frac{1}{y}\frac{dy}{dx}=\frac{d}{dx}[cos x log (log x)]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-f460f92a6e38ab306a905e12e565c88c_l3.png)
=> 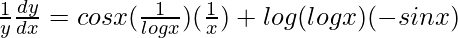
=> 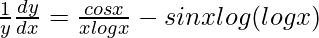
=> ![Rendered by QuickLaTeX.com \frac{dy}{dx}=y\left[\frac{cosx}{xlogx}-sinxlog(logx)\right]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-559206c12462333cbc6c6cb76a00e080_l3.png)
=> ![Rendered by QuickLaTeX.com \frac{dy}{dx}=(logx)^{cosx}\left[\frac{cosx}{xlogx}-sinxlog(logx)\right]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-2cff246d4330433b9cc8ebaabd49d5e2_l3.png)
Question 7. Differentiate y = (sin x)cos x with respect to x.
Solution:
We have,
=> y = (sin x)cos x
On taking log of both the sides, we get,
=> log y = log (sin x)cos x
=> log y = cos x log (sin x)
On differentiating both sides with respect to x, we get,
=> ![Rendered by QuickLaTeX.com \frac{1}{y}\frac{dy}{dx}=\frac{d}{dx}[cos x log (sin x)]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-799a0c4a7ec4b55bf2866dd87fb6db5f_l3.png)
=> 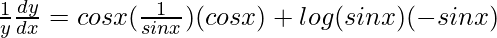
=> 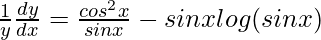
=> 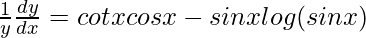
=> ![Rendered by QuickLaTeX.com \frac{dy}{dx}=y\left[cotxcosx-sinxlog(sinx)\right]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-ae8fe7e8dbf5ca75f61791993cbae939_l3.png)
=> ![Rendered by QuickLaTeX.com \frac{dy}{dx}=(sinx)^{cosx}\left[cotxcosx-sinxlog(sinx)\right]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-45ebf8560984dc01c35a20a2df578f40_l3.png)
Question 8. Differentiate y = ex log x with respect to x.
Solution:
We have,
=> y=ex log x
=> y = 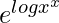
=> y = xx
On taking log of both the sides, we get,
=> log y = log xx
=> log y = x log x
On differentiating both sides with respect to x, we get,
=> 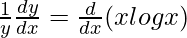
=> 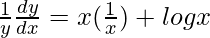
=> 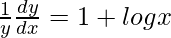
=> 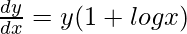
=> 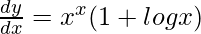
Question 9. Differentiate y = (sin x)log x with respect to x.
Solution:
We have,
=> y = (sin x)log x
On taking log of both the sides, we get,
=> log y = log (sin x)log x
=> log y = log x log (sin x)
On differentiating both sides with respect to x, we get,
=> ![Rendered by QuickLaTeX.com \frac{1}{y}\frac{dy}{dx}=\frac{d}{dx}[log x log (sin x)]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-c74accb7dfdd0915c67ba4f193c65839_l3.png)
=> 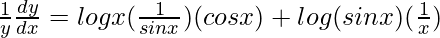
=> 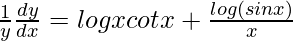
=> ![Rendered by QuickLaTeX.com \frac{dy}{dx}=y\left[logxcotx+\frac{log(sinx)}{x}\right]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-c7278db6acd2c13a8c9c180858fad8c5_l3.png)
=> ![Rendered by QuickLaTeX.com \frac{dy}{dx}=(sinx)^{logx}\left[logxcotx+\frac{log(sinx)}{x}\right]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-c66dca591f02928db0618d39ac717149_l3.png)
Question 10. Differentiate y = 10log sin x with respect to x.
Solution:
We have,
=> y = 10log sin x
On taking log of both the sides, we get,
=> log y = log 10log sin x
=> log y = log (sin x) log 10
On differentiating both sides with respect to x, we get,
=> ![Rendered by QuickLaTeX.com \frac{1}{y}\frac{dy}{dx}=\frac{d}{dx}[log (sin x) log 10]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-ab95d6a13cc197ef34a8e24f01c963eb_l3.png)
=> ![Rendered by QuickLaTeX.com \frac{1}{y}\frac{dy}{dx}=log10\frac{d}{dx}[log(sinx)]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-b222207c6b8be877336e26743594ee16_l3.png)
=> 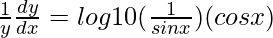
=> 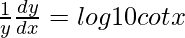
=> 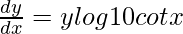
=> ![Rendered by QuickLaTeX.com \frac{dy}{dx}=10^{logsinx}[log10cotx]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-9f3cdaee8d7798a0fbeafe8fac321ca0_l3.png)
Question 11. Differentiate y = (log x)log x with respect to x.
Solution:
We have,
=> y = (log x)log x
On taking log of both the sides, we get,
=> log y = log (log x)log x
=> log y = log x log (log x)
On differentiating both sides with respect to x, we get,
=> ![Rendered by QuickLaTeX.com \frac{1}{y}\frac{dy}{dx}=\frac{d}{dx}[log x log (log x)]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-c191a18c586becd364ba326f4c034f78_l3.png)
=> 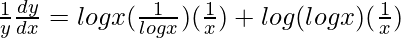
=> 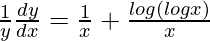
=> 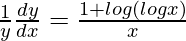
=> ![Rendered by QuickLaTeX.com \frac{dy}{dx}=\frac{y[1+log(logx)]}{x}](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-cd3a4d0805199cf5415d8d7d206693dc_l3.png)
=> ![Rendered by QuickLaTeX.com \frac{dy}{dx}=\frac{(logx)^{logx}[1+log(logx)]}{x}](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-ac1e9086234de4ad058e8566510b9408_l3.png)
Question 12. Differentiate 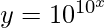 with respect to x.
with respect to x.
Solution:
We have,
=> 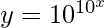
On taking log of both the sides, we get,
=> log y = log 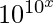
=> log y = 10x log 10
On differentiating both sides with respect to x, we get,
=> 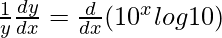
=> 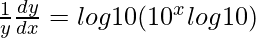
=> 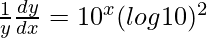
=> 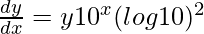
=> ![Rendered by QuickLaTeX.com \frac{dy}{dx}=10^{10^x}\left[10^x(log10)^2\right]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-8d6f8a5cfc70f0be1a6f241fc47d75fa_l3.png)
=> 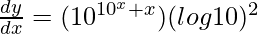
Question 13. Differentiate y = sin xx with respect to x.
Solution:
We have,
=> y = sin xx
=> sin−1 y = xx
On taking log of both the sides, we get,
=> log (sin−1 y) = log xx
=> log (sin−1 y) = x log x
On differentiating both sides with respect to x, we get,
=> 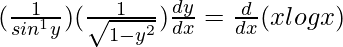
=> 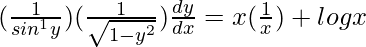
=> 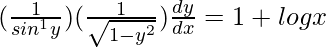
=> 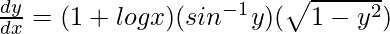
=> 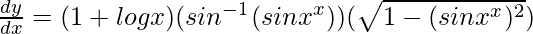
=> 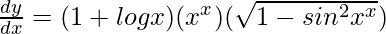
=> 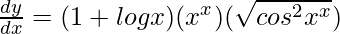
=> 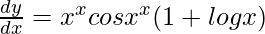
Question 14. Differentiate y = (sin−1x)x with respect to x.
Solution:
We have,
=> y = (sin−1x)x
On taking log of both the sides, we get,
=> log y = (sin−1x)x
=> log y = x log (sin−1x)
On differentiating both sides with respect to x, we get,
=> ![Rendered by QuickLaTeX.com \frac{1}{y}\frac{dy}{dx}=\frac{d}{dx}[x log (sin^{−1}x)]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-2c207294869bae670d250cc34ecb8c24_l3.png)
=> 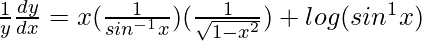
=> 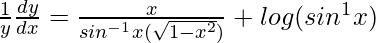
=> ![Rendered by QuickLaTeX.com \frac{dy}{dx}=y\left[\frac{x}{sin^{-1}x(\sqrt{1-x^2})}+log (sin^{−1}x)\right]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-d7738dac8fa7a2509aea0ffd9a67329c_l3.png)
=> ![Rendered by QuickLaTeX.com \frac{dy}{dx}=(sin^{-1}x)^x\left[\frac{x}{sin^{-1}x(\sqrt{1-x^2})}+log (sin^{−1}x)\right]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-b36c5886ab487fb97f3e6dc894e669d5_l3.png)
Question 15. Differentiate 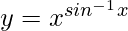 with respect to x.
with respect to x.
Solution:
We have,
=> 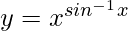
On taking log of both the sides, we get,
=> log y = log 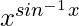
=> log y = sin−1x log x
On differentiating both sides with respect to x, we get,
=> 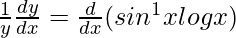
=> 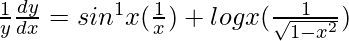
=> 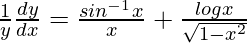
=> ![Rendered by QuickLaTeX.com \frac{dy}{dx}=y\left[\frac{sin^{-1}x}{x}+\frac{logx}{\sqrt{1-x^2}}\right]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-a2179284a5caa682e4e3a8ac1149d1c6_l3.png)
=> ![Rendered by QuickLaTeX.com \frac{dy}{dx}=x^{sin^{-1}x}\left[\frac{sin^{-1}x}{x}+\frac{logx}{\sqrt{1-x^2}}\right]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-4d6015adee3bf01ddd3b054560daf111_l3.png)
Question 16. Differentiate 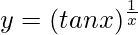 with respect to x.
with respect to x.
Solution:
We have,
=> 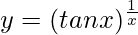
On taking log of both the sides, we get,
=> log y = log 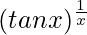
=> log y = 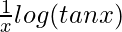
On differentiating both sides with respect to x, we get,
=> ![Rendered by QuickLaTeX.com \frac{1}{y}\frac{dy}{dx}=\frac{d}{dx}[\frac{1}{x}log(tanx)]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-542ce988dba7b34795daf0f4ded71b7d_l3.png)
=> 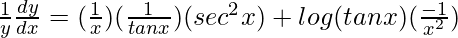
=> 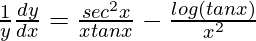
=> ![Rendered by QuickLaTeX.com \frac{dy}{dx}=y\left[\frac{sec^2x}{xtanx}-\frac{log(tanx)}{x^2}\right]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-9fda1762a041cf6c9936496e5a6b6a3c_l3.png)
=> ![Rendered by QuickLaTeX.com \frac{dy}{dx}=(tanx)^{\frac{1}{x}}\left[\frac{sec^2x}{xtanx}-\frac{log(tanx)}{x^2}\right]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-3025390bbbd13332e75310ac95a94ad6_l3.png)
Question 17. Differentiate 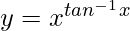 with respect to x.
with respect to x.
Solution:
We have,
=> 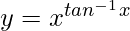
On taking log of both the sides, we get,
=> log y = log 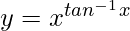
=> log y = tan−1 x log x
On differentiating both sides with respect to x, we get,
=> 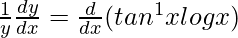
=> 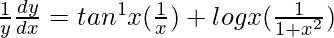
=> 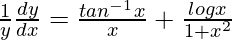
=> ![Rendered by QuickLaTeX.com \frac{dy}{dx}=y\left[\frac{tan^{-1}x}{x}+\frac{logx}{1+x^2}\right]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-f0bcec3d4ccc3b21ff9f50b0a9a0c085_l3.png)
=> ![Rendered by QuickLaTeX.com \frac{dy}{dx}=x^{tan^{-1}x}\left[\frac{tan^{-1}x}{x}+\frac{logx}{1+x^2}\right]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-72c133c0c9d35db3ef9f4f0432cefcec_l3.png)
Question 18. Differentiate the following with respect to x.
(i) y = xx √x
Solution:
We have,
=> y = xx √x
On taking log of both the sides, we get,
=> log y = log (xx √x)
=> log y = log xx + log √x
=> log y = x log x + 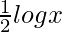
On differentiating both sides with respect to x, we get,
=> 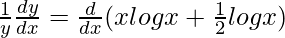
=> 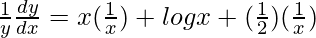
=> 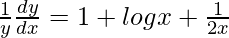
=> 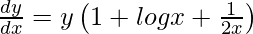
=> 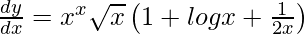
(ii) 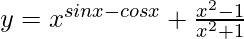
Solution:
We have,
=> 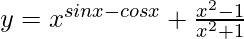
=> 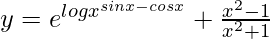
=> 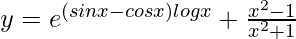
On differentiating both sides with respect to x, we get,
=> 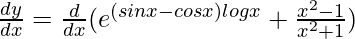
=> ![Rendered by QuickLaTeX.com \frac{dy}{dx}=(e^{(sinx-cosx)logx})[(sinx-cosx)\frac{1}{x}+logx(cosx+sinx)]+\frac{(x^2+1)(2x)-(x^2-1)(2x)}{(x^2+1)^2}](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-223abb9a2f9b45a3be317e0aa2f276b3_l3.png)
=> ![Rendered by QuickLaTeX.com \frac{dy}{dx}=(x^{sinx-cosx})[\frac{sinx-cosx}{x}+logx(cosx+sinx)]+\frac{2x(x^2+1-x^2+1)}{(x^2+1)^2}](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-439d71cf664de3a9a38b7a14a3b33cdb_l3.png)
=> ![Rendered by QuickLaTeX.com \frac{dy}{dx}=(x^{sinx-cosx})[\frac{sinx-cosx}{x}+logx(cosx+sinx)]+\frac{2x(2)}{(x^2+1)^2}](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-1e2f16c65a37d08d754ab3ab620c20f2_l3.png)
=> ![Rendered by QuickLaTeX.com \frac{dy}{dx}=(x^{sinx-cosx})[\frac{sinx-cosx}{x}+logx(cosx+sinx)]+\frac{4x}{(x^2+1)^2}](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-1f56636c74cc3d5018587874bc304a47_l3.png)
(iii) 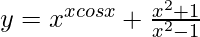
Solution:
We have,
=> 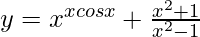
=> 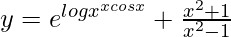
=> 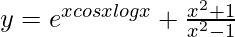
On differentiating both sides with respect to x, we get,
=> ![Rendered by QuickLaTeX.com \frac{dy}{dx}=(e^{xcosxlogx})[x((-sinx)logx+cosx(\frac{1}{x}))+cosxlogx]+\frac{(x^2-1)(2x)-(x^2+1)(2x)}{(x^2-1)^2}](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-b16fab40f634b4146074653c6c80b20d_l3.png)
=> ![Rendered by QuickLaTeX.com \frac{dy}{dx}=(e^{xcosxlogx})[-xsinxlogx+cosx+cosxlogx]+\frac{2x(x^2-1-x^2-1)}{(x^2-1)^2}](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-52257a2523a81560e320158658712d6d_l3.png)
=> ![Rendered by QuickLaTeX.com \frac{dy}{dx}=(e^{xcosxlogx})[-xsinxlogx+cosx(1+logx)]+\frac{2x(-2)}{(x^2-1)^2}](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-b56e31308f8b7e33095450e35e668bd2_l3.png)
=> ![Rendered by QuickLaTeX.com \frac{dy}{dx}=(e^{xcosxlogx})[cosx(1+logx)-xsinxlogx]-\frac{4x}{(x^2-1)^2}](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-db80cf67beba17c85c10879e7b5ea152_l3.png)
=> ![Rendered by QuickLaTeX.com \frac{dy}{dx}=x^{xcosx}[cosx(1+logx)-xsinxlogx]-\frac{4x}{(x^2-1)^2}](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-781b8b7743a1ab626c8b5e8ea46d8f76_l3.png)
(iv) y = (x cos x)x + (x sin x)1/x
Solution:
We have,
=> y=(x cos x)x + (x sin x)1/x
=> 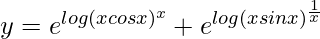
=> 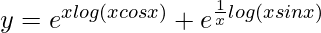
=> 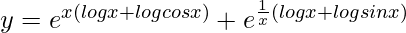
On differentiating both sides with respect to x, we get,
=> ![Rendered by QuickLaTeX.com \frac{dy}{dx}=(e^{x(logx+logcosx)})[x(\frac{1}{x}+(\frac{1}{cosx})(-sinx))+log(xcosx)(1)]+ (e^{\frac{1}{x}(logx+logsin x)})[\frac{1}{x}(\frac{1}{x}+(\frac{1}{sinx})(cosx))+log(xsinx)(\frac{-1}{x^2})]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-44ceed2b2c359e2817041dccfa8aaa43_l3.png)
=> ![Rendered by QuickLaTeX.com \frac{dy}{dx}=(e^{x(logx+logcosx)})[1-xtanx+log(xcosx)]+ (e^{\frac{1}{x}(logx+logsin x)})[\frac{1}{x^2}+\frac{1}{xcotx}-\frac{log(xsinx)}{x^2}]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-87bce6c0b324a1d4627de24314359085_l3.png)
=> ![Rendered by QuickLaTeX.com \frac{dy}{dx}=(e^{x(logx+logcosx)})[1-xtanx+log(xcosx)]+ (e^{\frac{1}{x}(logx+logsin x)})[\frac{1-log(xsinx)+xcotx}{x^2}]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-8643e9cee8dd0ea097e2a78d6ed2132f_l3.png)
=> ![Rendered by QuickLaTeX.com \frac{dy}{dx}=(xcosx)^x[1-xtanx+log(xcosx)]+ (xsinx)^{\frac{1}{x}}[\frac{1-log(xsinx)+xcotx}{x^2}]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-1bbab61ca26c43426c805b9d4e9e56be_l3.png)
(v) 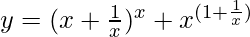
Solution:
We have,
=> 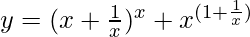
=> 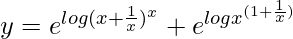
=> 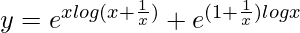
On differentiating both sides with respect to x, we get,
=> ![Rendered by QuickLaTeX.com \frac{dy}{dx}=(e^{xlog(x+\frac{1}{x})})[x(\frac{1}{x+\frac{1}{x}})(1-\frac{1}{x^2})+log(x+\frac{1}{x})]+(e^{(1+\frac{1}{x})logx})[(1+\frac{1}{x})(\frac{1}{x})+logx(\frac{-1}{x^2})]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-8d4f426b1ffa47c5bb9e14bd6ce00fa4_l3.png)
=> ![Rendered by QuickLaTeX.com \frac{dy}{dx}=(e^{xlog(x+\frac{1}{x})})[(\frac{x-\frac{1}{x}}{x+\frac{1}{x}})+log(x+\frac{1}{x})]+(e^{(1+\frac{1}{x})logx})[\frac{1}{x}+\frac{1}{x^2}-logx(\frac{1}{x^2})]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-202c59a9a42e1ce050b0c9185420d964_l3.png)
=> ![Rendered by QuickLaTeX.com \frac{dy}{dx}=(x+\frac{1}{x})^x[\frac{x^2-1}{x^2+1}+log(x+\frac{1}{x})]+x^{1+\frac{1}{x}}[\frac{1}{x}+\frac{1}{x^2}-logx(\frac{1}{x^2})]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-f804ee5dbb5b36fb47ec2a641e4aa7a3_l3.png)
=> ![Rendered by QuickLaTeX.com \frac{dy}{dx}=(x+\frac{1}{x})^x[\frac{x^2-1}{x^2+1}+log(x+\frac{1}{x})]+x^{1+\frac{1}{x}}[\frac{1}{x}+\frac{1}{x^2}-\frac{logx}{x^2}]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-cab83f3a31ab56c9da1a935a79fd47b4_l3.png)
=> ![Rendered by QuickLaTeX.com \frac{dy}{dx}=(x+\frac{1}{x})^x[\frac{x^2-1}{x^2+1}+log(x+\frac{1}{x})]+x^{1+\frac{1}{x}}(\frac{x+1-logx}{x^2})](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-6c026cac9888528f0eb3578fe100f6b2_l3.png)
(vi) y = esin x + (tan x)x
Solution:
We have,
=> y = esin x + (tan x)x
=> 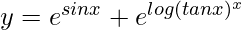
=> 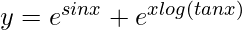
On differentiating both sides with respect to x, we get,
=> 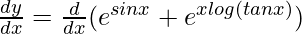
=> ![Rendered by QuickLaTeX.com \frac{dy}{dx}=(e^{sin x})(cosx) + (e^{xlogtanx})\left[x(\frac{1}{tanx})(sec^2x)+log(tanx)\right]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-7256857bf8992dfb2821a640d3e870b0_l3.png)
=> ![Rendered by QuickLaTeX.com \frac{dy}{dx}=e^{sin x}cosx+(tanx)^x\left[\frac{xsec^2x}{tanx}+log(tanx)\right]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-a7b03f81fbf2a47a577ff9b838ff0349_l3.png)
(vii) y = (cos x)x + (sin x)1/x
Solution:
We have,
=> y = (cos x)x + (sin x)1/x
=> 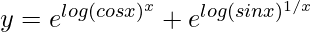
=> 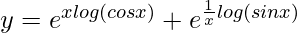
On differentiating both sides with respect to x, we get,
=> ![Rendered by QuickLaTeX.com \frac{dy}{dx}=(e^{xlog(cos x)})[x(\frac{1}{cosx})(-sinx)+log(cosx)] + (e^{\frac{1}{x}log(sin x)})[\frac{1}{x}(\frac{1}{sinx}(cosx))+log(sinx)(-\frac{1}{x^2})]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-ab41de374063ad33774b84d648fa4e5e_l3.png)
=> ![Rendered by QuickLaTeX.com \frac{dy}{dx}=(e^{xlog(cos x)})[-xtanx+log(cosx)] + (e^{\frac{1}{x}log(sin x)})[\frac{cotx}{x}-\frac{log(sinx)}{x^2}]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-fcbf3a82196abfc4eabab14e892709a2_l3.png)
=> ![Rendered by QuickLaTeX.com \frac{dy}{dx}=(cosx)^x[-xtanx+log(cosx)] + (sinx)^{\frac{1}{x}}[\frac{cotx}{x}-\frac{log(sinx)}{x^2}]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-bffa488bff9feee92bdbd037594bf2a7_l3.png)
(viii) 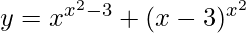 , for x > 3
, for x > 3
Solution:
We have,
=> 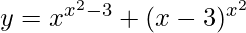
=> 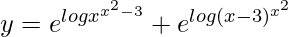
=> 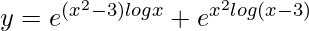
On differentiating both sides with respect to x, we get,
=> ![Rendered by QuickLaTeX.com \frac{dy}{dx}=(e^{(x^2-3)logx})[(x^2-3)(\frac{1}{x})+logx(2x)]+(e^{x^2log(x-3)})[x^2(\frac{1}{x-3})+log(x-3)(2x)]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-91b6f8b9b455b02faaaa800c46a3d1de_l3.png)
=> ![Rendered by QuickLaTeX.com \frac{dy}{dx}=(e^{(x^2-3)logx})[\frac{x^2-3}{x}+2xlogx]+(e^{x^2log(x-3)})[\frac{x^2}{x-3}+2xlog(x-3)]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-a71a371f579d61f49fa6c639d1b02e40_l3.png)
=> ![Rendered by QuickLaTeX.com \frac{dy}{dx}=x^{x^2-3}[\frac{x^2-3}{x}+2xlogx]+(x-3)^{x^2}[\frac{x^2}{x-3}+2xlog(x-3)]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-f28afd019bb0fd4a600c586e3fe5e0c9_l3.png)
Question 19. Find dy/dx when y = ex + 10x + xx.
Solution:
We have,
=> y = ex + 10x + xx
=> 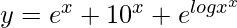
=> 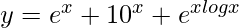
On differentiating both sides with respect to x, we get,
=> 
=> ![Rendered by QuickLaTeX.com \frac{dy}{dx}=e^x+10^xlog10+e^{xlogx}[x(\frac{1}{x})+logx]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-90aaf2fc639dea61ebe9644222761cbd_l3.png)
=> 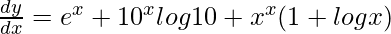
=> 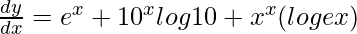
Question 20. Find dy/dx when y = xn + nx + xx + nn.
Solution:
We have,
=> y = xn + nx + xx + nn
=> 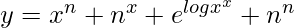
=> 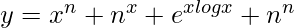
On differentiating both sides with respect to x, we get,
=> 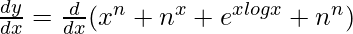
=> ![Rendered by QuickLaTeX.com \frac{dy}{dx}=nx^{n-1}+n^xlogn+e^{xlogx}[x(\frac{1}{x})+logx]+0](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-51acac165767ab765e27698ac52f4dc6_l3.png)
=> 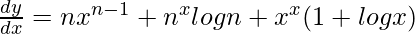
=> 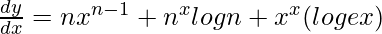
Like Article
Suggest improvement
Share your thoughts in the comments
Please Login to comment...