Mathematics is an important subject in CBSE Class 12th Board Exam. There is a common misunderstanding among students that Math is a complex subject. If students will plan their preparation and revision in right direction, they can score well in Mathematics.
For this Purpose, We have curated the Chapter Wise CBSE Class 12th Math Notes 2024 for you below.

Our Class 12th Math NCERT Notes are written in simple language and cover nearly all the chapters as per CBSE Class 12th Math Syllabus. Preparing from our Revision Notes will assist students in achieving high grades in their 12th-grade exams as well as exams such as JEE Mains and JEE Advanced.
CBSE Class 12th Maths Notes – Chapters Wise
All the Chapters covered in Class 12th Maths NCERT textbooks are listed below. Below is the list of major topics that have been covered in Class 12th Maths NCERT textbooks and the Class 12 CBSE Maths Syllabus.
Download CBSE Class 12 Math Notes PDF
Click on the link below to download the CBSE Class 12th Math notes.
CBSE Class 12 Math Notes PDF
|
|
|---|
Removed Chapters from NCERT Class 12th Maths Textbook (2023-2024)
The most recent CBSE Class 12th Maths syllabus has been updated and reduced by 30% for the upcoming CBSE Board Exam 2024. You can find the list of all removed chapters in the table below.
Chapter Name
| Deleted Topics
|
|---|
Relation and Function
| composite functions, the inverse of a function
|
Trigonometry Function
| Graphs of inverse trigonometric functions, Elementary properties of inverse trigonometric functions
|
Matrices
| Existence of non-zero matrices whose product is the zero matrixes; Concept of elementary row and column operations; Proof of the uniqueness of inverse, if it exists.
|
Determinants
| Properties of determinants; Consistency, inconsistency, and the number of solutions of a system of linear equations by examples.
|
Continuity and Differentiability
| Rolle’s and Lagrange’s Mean Value Theorems (without proof) and their geometric interpretation
|
Application of Derivatives
| Rate of change of bodies, use of derivatives in approximation.
|
Integrals
| ∫ √?x2 + ?? + ? dx, ∫(?? + ?)√??2 + ?? + ? dx and Definite integrals as a limit of a sum
|
Application of Integrals:
| Area between any of the two above-said curves.
|
Differential Equations
| Formation of differential equation whose general solution is given. Solutions of linear differential equation of the type: dx/dy+px=q, where p and q are functions of y or constants.
|
Vector
| Scalar triple product of vectors
|
Three-Dimensional Geometry
| Angle between (i) two lines, (ii) two planes, (iii) a line and a plane.
|
Linear Programming
| The mathematical formulation of L.P. problems (unbounded).
|
Probability
| Mean and variance of the random variable. Binomial probability distribution
|
Chapter 1: Relations and Functions
The term ‘relation’ in mathematics is derived from the English language’s definition of relationship, which states that two objects or quantities are linked if there is an observable connection or relation between them. This Class 12 Chapter 1 might be very confusing, therefore students can even use the strategies to improve their learning.
Resources for CBSE Class 12th Maths Notes Chapter 1
|
|---|
|
Chapter 1: Relations and Functions – Important formulae
- Relation- An Empty relation R in X, can be defined relation as: R = φ ⊂ X × X
- An Equivalence relation R in X is defined as a relation that can represent all the three types of relations: Reflexive, Symmetric, and Transitive relations.
- Symmetric relation R in X: (a, b) ∈ R ⇒ (b, a) ∈ R.
- Reflexive relation R in X: (a, a) ∈ R, ∀ a ∈ X.
- Transitive relation R in X: (a, b) ∈ R and (b, c) ∈ R, ⇒ (a, c) ∈ R.
- While, the Universal relation R in X: R = X × X.
- Function- Depending on the conclusion obtained functions f: X → Y can be of different types like,
- One-one or injective function: If f(x1) = f(x2) ⇒ x1 = x2 ∀ x1, x2 ∈ X.
- Onto or surjective function: If y ∈ Y, ∃ x ∈ X such that f(x) = y.
- One-one and onto or bijective function: if f follows both the one-one and onto properties.
- Invertible function: If ∃ g: Y → X such that gof = IX and fog = IY. This can happen only if f is one-one and onto.
Also Read
Chapter 2: Inverse Trigonometric Functions
The Chapter 2 Inverse Trigonometric Functions covers a variety of subjects, including notes based on basic concepts of inverse trigonometric functions, properties of inverse trigonometric functions, and miscellaneous examples. These principles are well-explained with examples.
In calculus, inverse trigonometric functions are essential because they are used to define various integrals. Inverse trigonometric functions have applications in science and engineering.
Inverse Trigonometric Functions gives an account of various topics such as the graphs of inverse trigonometric functions, different properties of inverse trigonometric functions, along with their domain, range, and other important attributes.
Inverse Trigonometry Functions |
|---|
|
|
|
More Resources for CBSE Class 12th Maths Notes Chapter 2
|
|
Here is the list of some important formulas covered in CBSE Class 12 Chapter 2: Inverse Trigonometric Functions.
- y = sin−1x ⇒ x = sin y
- x = sin y ⇒ y = sin−1x
- sin−1(1/x) = cosec−1x
- cos−1(1/x) = sec−1x
- tan−1(1/x) = cot−1x
- cos−1(−x) = π−cos−1x
- cot−1(−x) = π−cot−1x
- sec−1(−x) = π−sec−1x
- sin−1(−x) = −sin−1x
- tan−1(−x) = −tan−1x
- cosec−1(−x) = −cosec−1x
- tan−1x + cot−1x = π/2
- sin−1x + cos−1x = π/2
- cosec−1x + sec−1x = π/2
- 2tan−1x = sin−1{2x / 1+x2} = cos−1{1−x2}/{1+x2}
- 2tan−1x = tan−1{2x / (1−x2)}
- tan−1x + tan−1y = tan−1{(x + y) / (1−xy)}; xy < 1
- tan−1x + tan−1y = π + tan−1(x+y / 1−xy); xy > 1; x, y > 0
Chapter 3: Matrices
A Matrix is said to have an ordered rectangular array of functions or numbers. A matrix of order m × n consists of m rows and n columns. This chapter provides crucial knowledge of matrices that have applications in different areas such as business, sales, cost estimation, etc.
Matrices |
|---|
|
- Types of Matrices
- Equality of Matrices
|
|
|
- Multiplication of Matrices
- Non Commutativity of Matrix Multiplication (AB ≠ BA)
- Product of two non zero Matrix to get zero matrices
- Properties Multiplication of Matrices
- Associative Law
- Distributive Law
- Existence of Identity
|
|
|
|
|
|
Resources for CBSE Class 12th Maths Notes Chapter 3
|
|
Basic Operations of matrices
- kA = k[aij]m × n = [k(aij)]m × n
- – A = (– 1)A
- A – B = A + (– 1)B
- A + B = B + A
- (A + B) + C = A + (B + C); where A, B and C all are of the same order
- k(A + B) = kA + kB; where A and B are of the same order; k is constant
- (k + l)A = kA + lA; where k and l are the constant
If A = [aij]m × n and B = [bjk]n × p, then
- AB = C = m × p ; where cik = ∑nj=1aijbjk
- A.(BC) = (AB).C
- A(B + C) = AB + AC
- (A + B)C = AC + BC
If A= [aij]m × n, then A’ or AT = [aji]n × m also,
- (A’)’ = A
- (kA)’ = kA’
- (A + B)’ = A’ + B’
- (AB)’ = B’A’
Chapter 4: Determinants
Determinants clearly demonstrate the image of the determinant of a square matrix and the way to find it. Characteristics of determinants, minors and cofactors, and linear equations are important sub-topics that are explained in this chapter thoroughly.
This chapter is a continuation of the previous chapter of Matrices. This chapter helps to learn about the determinants, their properties, how determinants can be used to calculate the area of a triangle, and in solving a system of linear equations.
Determinants |
|---|
- Determinants
- Determinant of Matrix of Order One
- Determinant of Matrix of Order Two
- Determinant of Matrix of Order Three
|
|
|
|
|
|
|
Resources for CBSE Class 12th Maths Notes Chapter 4
|
|
Determinants – Important Formulas
- Definition of Determinant
- For a given matrix, A = [a11]1 × 1 its determinant is defined as det a11 or |a11| = a11
- For a 2 × 2 matrix, X =
 the determinant is defined as,
the determinant is defined as, 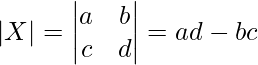
- For a 3 × 3 matrix,
 the determinant is defined as
the determinant is defined as
- Area of a triangle with vertices (x1, y1), (x2, y2) and (x3, y3) is given by
- Minor: If the matrix given is:
- The Minor of a12 will be the determinant:
- Cofactor: Cofactors are related to minors by a small formula, for an element aij, the cofactor of this element is Cij and the minor is Mij then, cofactor can be written as:
- Scalar Multiple Property of determinants: If each element of a row (or a column) of a determinant is multiplied by a constant k, then its value gets multiplied by k
- Sum Property of determinants: If some or all elements of a row or column can be expressed as the sum of two or more terms, then the determinant can also be expressed as the sum of two or more determinants.
- Let, A be a matrix of order n, then
Chapter 5: Continuity and Differentiability
The Chapter Continuity and Differentiability is the extension of the Differentiation of Functions studied in Class 11. Now, in this class, you will understand functions, such as polynomial and trigonometric functions. This chapter focuses on the ideas of continuity, differentiability, and their interrelations.
The topics covered in Chapter 5 Continuity and Differentiability are how to differentiate inverse trigonometric functions. In addition, you’ll learn about a new class of functions known as exponential and logarithmic functions. The derivatives of exponential and logarithmic functions, as well as logarithmic differentiation, will be covered.
This chapter also covers the ideas of function derivatives in terms of parametric forms and second-order derivatives and introduction to the two theorems given by Rolle and Lagrange.
Continuity and Differentiability |
|---|
- Continuity of Functions
- Discontinuity in Calculus
|
|
|
|
|
|
|
|
Resources for CBSE Class 12th Maths Notes Chapter 5
|
|
Continuity and Differentiability – Important Formulas
- Properties related to continuity of a function:
- (f±g)(x) = f(x)±g(x) is continuous.
- (f.g)(x) = f(x).g(x) is continuous.
- fg(x) = f(x)g(x) (whenever g(x)≠0 is continuous.
- Chain Rule: If f = v o u, t = u (x) and if both dt/dx and dv/dx exists, then:
- Rolle’s Theorem: If f: [a, b] → R is continuous on [a, b] and differentiable on (a, b) where as f(a) = f(b), then there exists some c in (a, b) such that f ′(c) = 0.
- Mean Value Theorem: If f : [a, b] → R is continuous on [a, b] and differentiable on (a, b). Then there exists some c in (a, b) such that
- f ′(c) = [ f(b)−f(a) ] / (b−a)
- Standard formulas for derivatives of a function:
- d/dx (sin−1x) = 1/√1−x2
- d/dx(cos−1x) = −1/√1−x2
- d/dx(tan−1x) = 1/√1+x2
- d/dx(cot−1x) = −1/√1+x2
- d/dx(sec−1x) = 1/x√1−x2
- d/dx(cosec−1x) = −1/x√1−x2
- d/dx (ex) = ex
- d/dx (log x) = 1/x
Chapter 6: Applications of Derivatives
Applications of Derivatives in Class 12 deals with the basic introduction of derivatives, how to determine the rate of change of quantities, find the minimum and maximum values of a function, and equations of tangents and normal to a curve.
Application of Derivatives |
|---|
|
|
|
|
|
- How to find Maxima and Minima?
- First Derivative Test
- Second Derivative Test
|
|
Resources for CBSE Class 12th Maths Notes Chapter 6
|
|
Applications of Derivatives – Important formulas
- Equation of tangent in point-slope form is
- (y – f(a))/(x – a) = f'(a)
- Equation of normal is,
- (y – f(a))/(x – a) = -1/f'(a)
- Second Derivative Test: When a function’s slope is zero at x, then the second derivative f” at that point is:
- f” < 0, if it is a maxima.
- f” > 0, if it is a minima.
Chapter 7: Integrals
The anti-derivative, also known as an integral, is introduced to students in CBSE Notes Class 12th Maths Integrals. Students are taught about the geometric representation of integrals as well as how to perform function integration using numerous methods and formulas. In addition, students are taught about definite integrals.
In this chapter, the methods to determine the function when its derivative is given and the area under a graph of a function are discussed. Basic properties of integrals and the fundamental theorem of calculus are also included in this chapter.
The most crucial part of this chapter is covered well versed in the below links. Such topics are various methods used to determine the integration of a function such as integration by substitution, integration using partial fractions, integration by parts, integration using trigonometric identities, integration of some integral functions, and definition and concept of definite integrals.
Along with Riemann sums with sigma notation, the Trapezoidal rule, Definite integral as the limit of a Riemann sum, Indefinite integrals, and some methods to determine definite integrals like Integration by U-substitution, Reverse chain rule are discussed in these notes for chapter 7 integrals.
Integrals |
|---|
|
|
|
- Integrals of Some Particular Functions
|
|
|
|
|
|
|
|
Resources for CBSE Class 12th Maths Notes Chapter 7 |
- Class 12 NCERT Solutions Maths Chapter 7
- Class 12 RD Sharma Solutions Integrals Chapter 1 and Chapter 2
- All important formulas for Class 12 Chapter 7
|
Integrals – Standard formulas
- ∫xndx = xn+1/(n+1) +C, where n≠−1.
- ∫cos x dx = sin x + C
- ∫sin x dx = −cos x + C
- ∫sec2x dx = tan x + C
- ∫cosec2x dx = −cot x + C
- ∫sec x tan x dx = sec x + C
- ∫cosec x cot x dx = −cosec x + C
- ∫dx / √1−x2 = sin−1x + C
- ∫dx / √1−x2 = -cos−1x + C
- ∫dx / 1+x2 = tan−1 x + C
- ∫dx / 1+x2 = −cot−1x + C
- ∫ex dx = ex + C
- ∫ax dx = axlog a + C
- ∫dx / x√x2−1 = sec−1x + C
- ∫dx / x√x2−1 = −cosec−1x + C
- ∫1 / x dx = log |x| + C
Chapter 8: Applications of Integrals
Through this chapter Applications of Integrals, we’ll be continuing to discuss integrals. A different application of Integrals like area under simple curves, area of the region bounded by a curve and a line, the area between two curves, and miscellaneous examples.
From the below-given links, students can access the chapter-wise notes explaining the concepts from this chapter. This chapter also included topics like how to find the area of different geometrical figures such as circles, parabolas, and ellipses.
Application of Integrals |
|---|
|
|
|
|
Resources for CBSE Class 12th Maths Notes Chapter 8
|
|
Applications of Integrals – Important formulas
- The area enclosed by the curve y = f (x) ; x-axis and the lines x = a and x = b (b > a) is given by the formula:
- Area = ∫bay dx=∫baf(x) dx
- Area of the region bounded by the curve x = φ (y) as its y-axis and the lines y = c, y = d is given by the formula:
- Area = ∫dcx dy=∫dcϕ(y) dy
- The area enclosed in between the two given curves y = f (x), y = g (x) and the lines x = a, x = b is given by the following formula:
- Area = ∫ba[f(x)−g(x)]dx
- where, f(x) ≥ g(x) in [a,b].
- If f (x) ≥ g (x) in [a, c] and f (x) ≤ g (x) in , a < c < b, then:
- Area = ∫ca[f(x)−g(x)]dx+∫bc[g(x)−f(x)]dx
Chapter 9: Differential Equations
In this Chapter Differential Equations, students will be introduced to the concept of differential equations, basic concepts related to differential equations, the degree of a differential equation, the order of a differential equation, and general and particular solutions of a differential equation.
The next section of the unit covers the formation of a differential equation, first-degree differentiable equations, and methods of solving first-order, These concepts of differential equations and how to find solutions to a differential equation are very useful in various applications in Physics, and Economics.
Differential Equations |
|---|
|
- Solution of Differential Equations
|
- Formation of Differential Equations
|
- Methods of Solving Differential Equations
|
Resources for CBSE Class 12th Maths Notes Chapter 9
|
|
Differential Equations – Important Concepts
- Order of differential equation: In the given differential equation, the greatest order of the derivative existent in the dependent variable with respect to the independent variable.
- General and Particular Solution of a Differential Equation: The general solution of the differential equation is the solution that contains arbitrary constants. A particular solution of the differential equation is one that is free of arbitrary constants and is produced from the general solution by assigning particular values to the arbitrary constants.
- Methods of Solving First Order, First Degree Differential Equations
- Differential equations with variables separable
- Homogeneous differential equations
- Linear differential equations
Chapter 10: Vector Algebra
In this chapter, the concepts of Vector algebra, how to find the position vector of a point, geometrical interpretation of vectors, and scalar and cross product of vectors are discussed. These concepts have great importance in higher education (engineering and technology).
Major topics covered in this chapter cover how to find position vector, some basic concepts related to vector algebra, direction cosines, types of vectors such as zero vector, unit vector, collinear vector, equal vector, negative of a vector, addition of vectors, properties of vector addition.
Along with the multiplication of a vector by a scalar, components of a vector, vector joining two points, section formula, a product of two vectors, scalar or dot product of two vectors, properties of scalar product, projection of a vector on a line, vector or cross product of two vectors are discussed in this chapter.
Vector Algebra |
|---|
|
- Types of Vectors
- Zero Vectors
- Unit Vectors
- Equal Vectors
- Negative of a Vector
- Co-Initial Vectors
- Collinear Vectors
- Parallel Vectors
- Orthogonal Vectors
|
- Addition of Vectors
- Triangle Law of Vector Addition
- Parallelogram Law of Vector Addition
- Properties of Vector Addition
- Commutative Property
- Associative Property
- Identity of Addition
- Additive Inverse
|
- Multiplication of Vector by a Scalar
|
|
|
Resources for CBSE Class 12th Maths Notes Chapter 10 |
|
Vector Algebra – important formulas
- Commutative Law: a + b = b + a
- Associative Law: a+ (b + c) = (a + b) + c
- Dot Product: (a • b )= |a| |b| cos θ
- Cross Product: (a× b )= |a| |b| sin θ
- k (a + b )= ka + kb
- Additive Identity: a + 0 = 0 + a
Chapter 11: Three-dimensional Geometry
Based on the vector algebra discussed in the previous chapter, here are the concepts like, how it can be applied to three-dimensional geometry. Also, the introduction to topics like direction cosines and direction ratios, cartesian and vector equations of a line, and how to find the shortest distance between two lines using these concepts are discussed in this part.
Three-Dimensional Geometry |
|---|
|
- Equation of a Line in 3D
- Equation of line pass through a point and parallel to any vector
- Equation of line passing through two points
|
|
|
- Plane
- Equation of Plane in Normal Form
- Equation of Plane passing through a point and perpendicular to given vector
- Plane Through three non-collinear Points
- Plane Passing through the intersection of two Plane
|
- Coplanarity of Two Lines
- Vector Form
- Cartesian Form
|
- Angle Between Two Planes
- Vector Form
- Cartesian Form
|
- Distance of a Point from a Planes
- Vector Form
- Cartesian Form
|
- Angle Between a Line and a Plane
- Vector Form
- Cartesian Form
|
Resources for CBSE Class 12th Maths Notes Chapter 11
|
- Class 12 NCERT Solutions Maths Chapter 11
- Class 12 RD Sharma Solutions Three-dimensional Geometry Chapter 1, Chapter 2 and Chapter 3
- All important formulas for Class 12 Chapter 11
|
Three-dimensional Geometry – important formulas
- Cartesian equation of a plane: lx + my + nz = d
- Distance between two points P(x1, y1, z1) and Q(x2, y2, z2): PQ = √ ((x1 – x2)2 + (y1 – y2)2 + (z1 – z2)2)
Chapter 12: Linear Programming
This chapter is a continuation of the concepts of linear inequalities and the system of linear equations in two variables studied in the previous class.
This chapter helps to learn how these concepts can be applied to solve real-world problems and how to optimize the problems of linear programming so that one can maximize resource utilization, minimize profits, etc.
Linear Programming |
|---|
|
- Solution of Linear Programming Problem
- Feasible Region
- Non-Feasible Region
- Optimal Solution
|
- Corner Point Method to Solve LPP
|
|
- Types of Linear Programming Problems
- Manufacturing Problem
- Diet Problem
- Transportation Problem
- Allocation Problem
|
Resources for CBSE Class 12th Maths Notes Chapter 12
|
|
Linear Programming – Important concepts
- The common region determined by all the constraints including the non-negative constraints x ≥ 0, y ≥ 0 of a linear programming problem is called the feasible region (or solution region) for the problem.
- Any point in the feasible region that gives the optimal value (maximum or minimum) of the objective function is called an optimal solution.
Chapter 13: Probability
This chapter deals with probability, but the basics of the concept of probability are already introduced in early classes. This chapter in the present class helps to learn about conditional probability.
Further, the topics like Bayes’ theorem, independence of events, the probability distribution of random variables, mean and variance of a probability distribution, and Binomial distribution are discussed in this chapter.
Probability |
|---|
|
|
|
|
|
|
|
|
|
|
More Resources for CBSE Class 12th Maths Notes Chapter 13 |
|
Probability – Important formulas
- The conditional probability of an event E holds the value of the occurrence of the event F as:
- P(E|F) = E ∩ F / P(F), P(F)≠0
- Total Probability: Let E1 , E2 , …. , En be the partition of a sample space and A be any event; then,
- P(A) = P(E1) P (A|E1) + P (E2) P (A|E2) + … + P (En) . P(A|En)
- Bayes Theorem: If E1 , E2 , …. , En are events constituting in a sample space S; then,
- P(Ei|A) = P(Ei) P(A|Ei) / ∑nj=1 P(Ej) P(A|Ej)
Important Resources for CBSE Class 12th Maths
CBSE Class 12th Maths Notes – FAQs
What are the major topics covered in Class 12th Maths Chapter 5 Continuity and Differentiability?
The major topics covered in Chapter 5 Continuity and Differentiability are Continuity of a function, and performing algebraic operations on continuous functions. Other topics included which are essential for exams are finding the derivatives of composite, implicit, trigonometric, exponential, and logarithmic functions, differentiation of functions in parametric form, second-order derivatives, mean value theorem as well as the chain rule for differentiation.
What are some important tips to study Chapter 9 Differential Equations in Class 9?
The CBSE Class 12th Maths Notes for Chapter 9 may guide students in overcoming difficulty and trying to understand calculus concepts. Students can use the study tips listed below to help them speed up their learning.
- Before diving into differential equations, make sure you’ve completed the previous chapters.
- Make a list of formulas and take notes.
- Practice on a regular basis.
How these CBSE Class 12th Maths Notes are helpful for students in their board exams?
When attempting board exams, students must prepare their papers in a format that may be easily understood by the persons who will be correcting them. The NCERT solutions include a detailed and step-by-step explanation that teaches students how to solve any problem. Because each step is assigned a set of marks, learners who follow the pattern of these NCERT solutions are certain to receive the highest possible grade.
Share your thoughts in the comments
Please Login to comment...