Integrals: An integral in mathematics is a continuous analog of a sum that is used to determine areas, volumes, and their generalizations. Performing integration is the process of computing an integral and is one of the two basic concepts of calculus.
Integral in Calculus is the branch of Mathematics that deals with finding integrals of the given functions. The branch of calculus that deals with integral is called Integral Calculus.
In this article, we will learn about the Integral definition, types, formulas, properties, examples solved problems, etc.
What are Integrals?
The term “integral” originated from Middle English, deriving from Medieval Latin integralis, meaning “making up a whole,” which itself stems from the Latin integer, signifying “untouched, entire.”
There are three types of integrals:
- Indefinite Integrals: These integrals are not defined with specific upper and lower limits. They represent a family of functions whose derivatives are equal to the given function f(x). Indefinite integrals return a function of the independent variable.
- Definite Integrals: Denoted by ∫ab f(x) dx, where a is the lower limit and b is the upper limit of integration. Definite integrals compute the net area between the curve y=f(x) and the x-axis over the interval [a,b].
- Improper Integrals: These integrals involve functions that are unbounded or have infinite discontinuities within the interval of integration. Improper integrals require special treatment, often involving limits, to determine convergence or divergence.
Integrals Definition
Integral in Maths is defined as the numerical value or a function that is calculated using the inverse process of differentiation.
Suppose the differentiation of F(x) is f(x) then, integral of f(x) is F(x) + c. Integrals are also called the antiderivative of the function. Integration is explained using the example added below,
Example: Given function f(x) = 2x3 + 3x
Derivative of f(x) = f'(x) = d/dx{2x3 + 3x}
f'(x) = 6x + 3
Integration of f'(x) = ∫ f'(x) dx = f(x)
f(x) = 2x3 + 3x + c
Integrals Definition
In mathematics, we define the integration of the function or integral of the function as the inverse operation of differentiation. The integral of the function is also called the antiderivative of the function.
Types of Integrals
Integral are used to solve various types of problems in Calculus, Physics, etc. The integrals are of two types, that are,
- Indefinite Integrals
- Definite Integrals
- Improper Integrals
Indefinite Integrals
Indefinite Integrals are used to find the integrals of the function when the limit of the integration is given. While solving the indefinite integrals we always have the constant of integration in the solution. The integration of the function g(x) is calculated as,
∫ g(x) = G(x) + c
Definite Integrals
Definite Integrals is the integral of the function with the limit of the integration given. Definite integrals gives the value of the function in numerical form. The definite integral of the function is given as,
∫ab g(x) dx = G(b) – G(a)
Improper Integrals
Improper integrals arise when the function being integrated is unbounded or has infinite discontinuities within the interval of integration. They are evaluated by considering limits as one or both of the integration limits approach infinity or approach points of discontinuity within the interval. Here’s a more detailed explanation along with examples:
1. Infinite Intervals
An improper integral with an infinite interval occurs when one or both of the integration limits are infinite.
- Example: Consider the function f(x)=1/x2 over the interval [1,∞).
∫1∞ 1/x2 dx
This integral represents the area under the curve f(x) from x=1 to x=∞. To evaluate it, we compute the limit:
limt → ∞ ∫1t 1/x2 dx
If the limit exists, the integral is said to converge; otherwise, it diverges.
2. Infinite Discontinuities
An improper integral with infinite discontinuities occurs when the function has a vertical asymptote or an infinite discontinuity within the interval of integration.
- Example: Consider the function g(x)= 1/√x over the interval [0,1].
∫01 1/√x dx
The function g(x) has a vertical asymptote at x=0. To evaluate the integral, we compute the limit:
lima → 0+ ∫a1 1/√x dx
If the limit exists, the integral converges; otherwise, it diverges.
3. Functions with Infinite Integrals
Some functions have integrals that extend to infinity due to their behavior.
- Example: The function h(x)=1/x over the interval [0,1].
∫01 1/x dx
This integral is improper because it becomes infinite at x=0. To evaluate it, we compute the limit:
lima → 0+∫a1 1/x dx
If the limit exists, the integral converges; otherwise, it diverges.
Integrals as Inverse of Differentiation
Consider derivatives of some functions given below,
- d/dx {x2} = 2x
- d/dx {sin (x)} = cos x
- d/dx {cos (x)} = – sin x
In the above equations, consider d/dx {x2} = 2x , here x2 is the anti-derivative for the function f'(x) = 2x. This follows for the above derivatives too.
Note that if these functions are added with constants, there is no difference to the derivatives as the derivative of a constant is zero.
- d/dx {x2 + C} = 2x
- d/dx {sin (x) + C} = cos x
- d/dx {cos (x) + C} = – sin x
So, it can be concluded that for any function, it’s anti-derivatives are infinite. For example, for the function f(x), let it’s anti-derivative be F(x),
∫ f(x) dx = F(x) + C
∫ denotes the integration. This will represent the integration operation over any function. The table below represents the symbols and meanings related to integrals.
| Symbols | Meaning |
|---|
| ∫ f(x) dx | Integral of f with respect to x |
| f(x) in ∫ f(x) dx | Integrand |
| x in ∫ f(x) dx | Variable of integration |
| Integral of f(x) | A function such that F'(x) = f(x) |
Properties of Integrals
Various properties of the integrals are:
- Linearity: The integral of a sum is the sum of the integrals. In other words, if f(x) and g(x) are integrable functions and a and b are constants, then:
∫ [af(x)+bg(x)] dx = a∫f(x)dx + b∫g(x)dx
- Additivity: The integral over a union of disjoint sets is the sum of the integrals over the individual sets.
- Constant Multiple Rule: If c is a constant, then:
∫c⋅f(x)dx = c⋅∫f(x)dx
- Integration by Parts: Integration by parts is a technique for integrating the product of two functions. The formula states:
∫udv = uv – ∫vdu
- Change of Variable: Also known as substitution, this technique involves changing the variable of integration. If u=g(x) is differentiable and f is continuous, then:
∫ f(g(x)) ⋅ g′(x)dx = ∫f(u)du
- Integration of Odd or Even Functions: The integral of an odd function over a symmetric interval is zero. The integral of an even function over a symmetric interval is twice the integral over half the interval.
- Fundamental Theorem of Calculus: This theorem establishes the relationship between differentiation and integration. It states that if f(x) is continuous on [a, b] and F(x) is an antiderivative of f(x), then:
∫ab f(x)dx = F(b) − F(a)
- Symmetry: If a function f(x) is even (symmetric about the y-axis), then its integral over the interval [−a, a] is twice the integral over the interval [0, a]. If f(x) is odd (antisymmetric about the origin), the integral over [−a, a] is zero.
Geometrical Interpretation of Integrals
Integrals are usually used for calculating the areas under the curve. Although there are formulas available, they are only available for standard shapes. Often arbitrarily complex shapes are encountered, and it is not possible to develop and remember a formula for every shape. Thus, integrals help in generalizing the method for calculating the areas and the volume. Consider a function f(x), the objective is to calculate the area of the function.
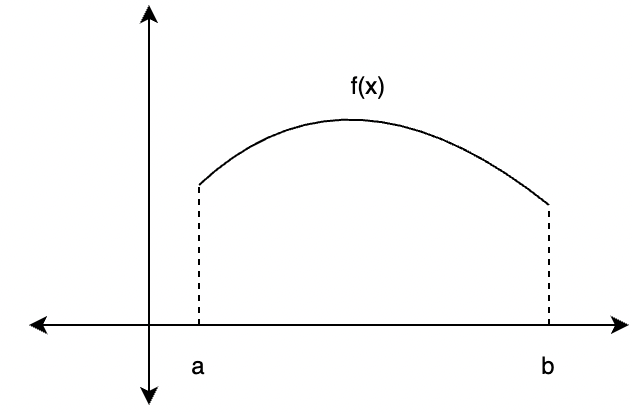
The function is divided up into different parts in the shape of rectangles, these parts add up and form the area. The width of each rectangle is
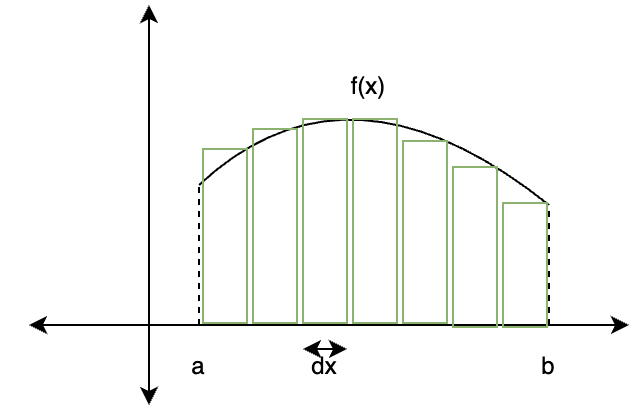
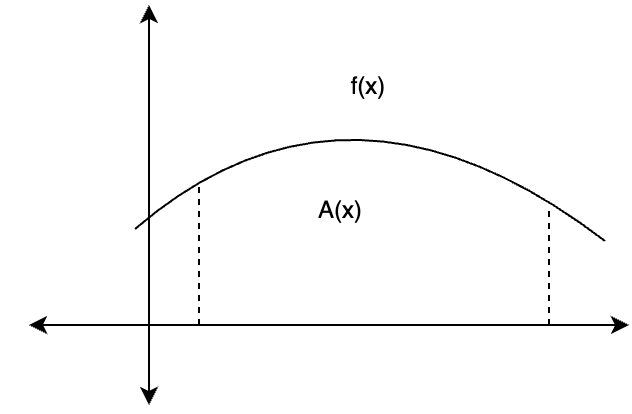
As the number of rectangles increase, the width of these rectangles becomes very small and can be denoted by “dx”. The area of each rectangle becomes f(x)dx. The total area is the sum of areas of all these small rectangles,
A(x) = Σ(x) = ∫ f(x) dx
This is explained in the image added below:
Various Integral formulas that are used to solve various types of integrals are:
- ∫ xn dx = x(n+1)/(n+1) + C, where n ≠ -1
- ∫ dx = x + C
- ∫ cosxdx = sinx + C
- ∫ sinx dx = -cosx + C
- ∫ sec2x dx = tanx + C
- ∫ cosec2x dx = -cotx + C
- ∫ sec2x dx = tanx + C
- ∫ secx tanxdx = secx + C
- ∫ cscx cotx dx = -cscx + C
- ∫-1/(1 + x2)= cot-1 x + C
- ∫1/(x√(x2 -1))= sec-1 x + C
- ∫-1/(x√(x2 -1))= cosec-1 x + C
- ∫1/(√(1 – x2))= sin-1 x + C
- ∫-1/(√(1 – x2))= cos-1 x + C
- ∫1/(1 + x2)= tan-1 x + C
- ∫1/(√(1 – x2))= sin-1 x + C
- ∫-1/(√(1 – x2))= cos-1 x + C
- ∫1/(1 + x2)= tan-1 x + C
- ∫ exdx = ex + C
- ∫dx/x = ln|x| + C
- ∫ ax dx = ax/ln a + C
Integrals Class 12
For Class 12 students studying calculus, integrals are a fundamental concept. Understanding integrals is crucial for solving various mathematical and real-world problems involving rates of change, accumulation, and measurement.
Also Check:
Solved Questions on Integrals
Question 1: Find the integral for the given function f(x) = 2sin(x) + 1.
Solution:
Given,
∫ f(x) dx = ∫ (2 sin x + 1) dx
= ∫ 2 sin x dx + ∫1 dx
= – 2 cos x + x + C
Question 2: Find the integral for the given function f(x) = 2x2 + 3x.
Solution:
Given,
∫ f(x) dx = ∫ (2x2 + 3x) dx
= 2 ∫ x2 dx + 3 ∫ x dx
= 2 (x3/3) + 3x + C
Question 3: Find the integral for the given function f(x) = x3 + 3x2 + x + 1.
Solution:
Given,
∫ f(x) dx = ∫ (x3 + 3x2 + x + 1)dx
= ∫x3 dx + 3∫x2 dx + ∫xdx + ∫1dx
= x4/4 + 3x3/3 + x2/2 + x + c
Question 4: Find the integral for the given function f(x) = sin(x) + 5cos(x).
Solution:
Given,
∫ f(x) dx = ∫ {sin x + 5 cos x}
= ∫ (sin x) dx + 5∫ cos x dx
= cos x + 5(-sin x) + c
= cos x – 5 sin x + c
Question 5: Find the integral for the given function f(x) = 5x-1 + 12.
Solution:
Given,
∫ f(x) dx = ∫ (5/x + 12) dx
= 5∫(1/x).dx + 12∫1.dx
= 5(ln x) + 12x + c
Question 6: Find the integral for the given function f(x) = (x + 1/x).
Solution:
Given,
∫ f(x) = ∫ (x + 1/x)dx
= ∫xdx + ∫(1/x)dx
= x2/2 + ln x + c
Integrals Practice Questions
Q1. Find the integral for the given function f(x) = (x + 1/x).
Q2. Find the integral for the given function f(x) = (2x3 + sin x).
Q3. Find the integral for the given function f(x) = (x2 + x + 1)/(x).
Q4. Find the integral for the given function f(x) = (t + 1)/(t2 – 1).
FAQs on Integrals
What is Integral Class 11?
Integral is the inverse operation of the differentiation, in differentiation we find the slope of the given curve at any point where as in integrals we find the area between the curve and the axis respectively.
What is the Integral of 2?
Integration is the reverse process of the differentiation. We know that integration of constant c is cx + d. So, ∫ 2 dx = 2x + c
What is integral of 3x?
Integration of x is x2/2.So, integration of ∫3x.dx = 3/2x2 + c.
What are Types of Integrals?
There are two types of Integrals, that are,
- Indefinite Integrals
- Definite Integrals
What is the Integral of Sin x?
Integral of Sin x is Cos x, i.e.
What is the Integral of Cos x?
Integral of Cos x is -Sin x, i.e.
What is the integral of 1?
The integral of the constant function f(x) = 1 with respect to x is simply x plus a constant of integration. Mathematically, it is represented as: ∫1dx = x+C where C is the constant of integration.
What is the integral of 0?
The integral of the constant function f(x) = 0 with respect to x is 0 plus a constant of integration. Mathematically, it is represented as: ∫0dx = C where C is the constant of integration.
How to calculate integrals?
Integrals can be calculated using various techniques, including:
- Analytical Methods: Such as integration by parts, substitution, partial fractions, and trigonometric substitutions.
- Numerical Methods: Such as the trapezoidal rule, Simpson’s rule, and numerical integration techniques.
- Software Tools: Many mathematical software packages and programming languages have built-in functions for calculating integrals numerically or symbolically.
What is integral formula?
- ∫ xn dx = x(n+1)/(n+1) + C, where n ≠ -1
- ∫ dx = x + C
- ∫ cosxdx = sinx + C
- ∫ sinx dx = -cosx + C
- ∫ sec2x dx = tanx + C
- ∫ cosec2x dx = -cotx + C
- ∫ sec2x dx = tanx + C
- ∫ secx tanxdx = secx + C
- ∫ cscx cotx dx = -cscx + C
- ∫-1/(1 + x2)= cot-1 x + C
- ∫1/(x√(x2 -1))= sec-1 x + C
- ∫-1/(x√(x2 -1))= cosec-1 x + C
- ∫1/(√(1 – x2))= sin-1 x + C
- ∫-1/(√(1 – x2))= cos-1 x + C
- ∫1/(1 + x2)= tan-1 x + C
- ∫1/(√(1 – x2))= sin-1 x + C
- ∫-1/(√(1 – x2))= cos-1 x + C
- ∫1/(1 + x2)= tan-1 x + C
- ∫ exdx = ex + C
- ∫dx/x = ln|x| + C
- ∫ ax dx = ax/ln a + C
Is integrals and integration same?
“Integrals” and “integration” are closely related terms but refer to slightly different concepts. “Integration” is the process of finding the integral of a function, while “integrals” refer to the results of that process. An integral can be either indefinite (representing a family of functions) or definite (representing a specific numerical value).
What is the symbol of integral?
The symbol used to denote integration is ∫ (long S). It represents the integral of a function with respect to a variable. For example, ∫f(x) dx represents the integral of the function f(x) with respect to the variable x. If limits of integration are specified, they are written as subscripts and superscripts, such as ∫ab f(x) dx, where a and b are the lower and upper limits, respectively.
Share your thoughts in the comments
Please Login to comment...