We know how to formulate equations of different degree, and it is used a lot in real life, but the question arises, is it always possible to convert a situation into an equation? Sometimes we get statements like, the number of Covid cases per day in Delhi has reached more than 10,000. This phrase “Less than”, “Greater than”, “less than or equal to” etc. Such phrases are difficult to translate into equations. For such cases, we need to learn how to make equations with inequalities in them. Let’s see this in detail.
What are Inequalities?
Let’s consider an example, Anil wants to buy some cold drinks. Each cold drink costs Rs 20, and he has a total of Rs 190 with him. Suppose he buys x cold drinks. What can be the maximum value of x? It can be represented in the form of an equation given below,
20x < 190
Two real expressions or real numbers related by the symbols “<“, “>”, “≤” or “≥” are called inequalities. The statement given above is an inequality. There are two types of inequalities:
- Numerical Inequalities: 3 < 5 or 7 > 5.
- Literal Inequalities: x > 5 and y < 7.
Some general examples of the inequalities are,
ax + by + c > 0 ….(1)
ax + by + c < 0 ….(2)
ax + by + c ≥ 0 ….(3)
ax + by + c ≤ 0 ….(4)
From the above equations, equations (1) and (2) are called strict inequalities, and (3) and (4) are called slack inequalities.
Solutions of Inequalities
Any solution to an inequality is the value of that variable which makes inequality a true statement. For example, suppose we have an inequality x < 5. In such a case, all the values of x which are less than 5 make this inequality a true inequality. While solving inequalities we need to keep some rules in mind,
- Equal numbers can be added or subtracted from both sides of the inequality.
- Both sides of an inequality can be multiplied (or divided) by the same positive number. But when both sides are multiplied or divided by a negative number, then the sign of inequality is reversed.
These operations do not affect the inequality and can be used to simplify the inequality for us.
Question: Solve the inequality 20x < 80 and show its solutions on a graph.
Solution:
We are given,
20x < 80
We know dividing the inequality by a positive number doesn’t change anything. Let’s divide the inequality with 20.
x < 4.
Now all the value less than 10 are solutions to this inequality. The figure below represents this solution on graph.

Graphical Representations of Inequalities in Two Variables
We saw the graph of a linear inequality in one variable. A linear equation in two variables represents a line that divides the plane into two parts. We call each part a half-plane. If the line is vertical, it will divide the plane into the left half-plane and the right half-plane and the non-vertical line divide the plane into the upper left half-plane and lower half-plane.


Any point in the Cartesian plane will either lie on the line or on either of the half-planes I and II.
Let’s say we have a line,
ax + by = c
Here, a ≠ 0 and b ≠ 0.
Now when we put any point (x, y) in the equation, there are three possible cases:
- ax + by > c
- ax + by < c
- ax + by = c
Let’s see all the cases
Case (i): ax + by > c
Let’s say b > 0. Consider a point(h, k) that satisfies the equation. Then,
ah + bk = c

Taking another arbitrary point (h, l). The figure below represents the two points along with the line. We know,
l > k
bl > bk
ah + bl > ah +bk
ah + bl > c
Thus, point (h, l) satisfy the property ax + by > c. Thus, all the points lying in half-plane II satisfy this inequality. For b < 0 also, this can be proved similarly.
Case (ii): ax + by = c
All the points satisfying the line, that is lying on the line satisfy this equation.
Case (iii): ax + by < c
All the remaining points, that is the points lying in the half-plane I satisfy this inequality.
Let’s see some problems with these concepts.
Sample Problems
Question 1: Solve the equation 5x + 3y > 6 graphically.
Solution:
First we need to draw the graph for 5x + 3y = 6. It can be done by bringing the equation in slope intercept form or the intercept form.

Now select a point arbitrarily to check. Let’s take (0,0).
Substituting this point (0,0) in the equation,
5(0) + 3(0) = 0 < 6.
Thus points in the lower half will satisfy 5x + 3y < 6. Thus, all the points satisfying the given equation will lie on upper half plane.

Question 2: Solve the equation 6x + 2y > 3 graphically.
Solution:
First we need to draw the graph for 6x + 2y = 3. It can be done by bringing the equation in slope intercept form or the intercept form.

Putting (0,0) in the equation,
6(0) + 2(0) = 0 < 3. Thus, the points in the upper half plane satisfy the given equation.
6x + 2y > 3

Question 3: Solve the equation x + y < 2 graphically.
Solution:
The equation given is, x + y < 2.
Putting the (0, 0) in the equation,
0 < 2.
This point satisfies the given equation. Thus, the graph will be,

Question 4: Solve the equation 3x – 5y < 20 graphically.
Solution:
As usual, we will take (0, 0) as the point we want to test on.
3(0) – 5(0) < 20.
This point satisfies the given inequality. Thus, the upper left half plane satisfies the inequality.

Question 5: Form the inequality from the graph given below.

Solution:
We can see this line is parallel to one of the axes. The equation of the line is,
x = 4
Now we want to form the linear inequality for the shaded region. (0,0) in the shaded region so we will check for that.
x = 0 < 4
Thus, the shaded region satisfies,
x < 4
Question 6: Form the inequality from the graph given below.

Solution:
From the graph, first let’s deduce the equation of the line. We can see the that x and y-axis intercepts are of length 4.
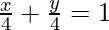
Now we need to figure out which condition is satisfied by the lower half plane. Let’s use (0,0) as it belongs to lower half plane. Substituting the value (0,0) in the equation,
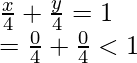
So,
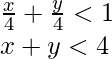
Share your thoughts in the comments
Please Login to comment...