Integration by U-substitution

Finding integrals is basically a reverse differentiation process. That is why integrals are also called anti-derivatives. Often the functions are straightforward and standard functions that can be integrated easily. It is easier to solve the combination of these functions using the properties of indefinite integrals. Sometimes functions are made up of compositions of two functions, these problems are harder to solve using the traditional way. In such cases, the U-substitution rule comes into play. Intuitively it is just the reverse of the chain rule. Let’s see this rule in detail. 

Indefinite Integrals

Consider a derivative function f'(x) defined and differentiable in an interval. Indefinite Integrals or anti-derivatives allow us to reverse the process of differentiation and calculate the function F(x) whose derivative is given to us. There are infinitely many anti-derivatives for any given derivative. Mathematically integrals are denoted by the symbol ∫

F(x)= ∫ƒ(x) + C

Where C is an arbitrary constant. The table below shows some conventions and phrases used in the integration with their meaning. 

Symbol/Term/Meaning	Meaning
∫f(x)dx	Integral of f with respect to x
f(x) in ∫f(x)dx	Integrand
x in ∫f(x)dx	Variable of integration
Integral of f(x)	A function such that F'(x) = f(x)

It is essential to keep in mind the integrals of some standard functions so that the integration becomes simpler and less time-consuming. Integrals of some standard functions are shown below. 

Function	Integral
xn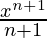
sin(x)	-cos(x)
cos(x)	sin(x)
ex	ex
sec2(x)	tan(x)
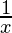	ln(x)

Properties of Integrals

Property 1: ∫kf(x)dx= k∫f(x)dx

Property 2: ∫f(x)± g(x)dx= ∫f(x)dx± ∫g(x)dx     

Property 3: ∫(f1(x)dx± f2(x)dx± f3(x)dx….)= ∫f1(x)dx± ∫f2(x)± ∫f3(x)dx…

U-Substitution Rule

Most often, integrals can be calculated using the properties and the formulas mentioned above. They allow us to calculate the simpler integrals in which integrands are usually a combination of some simple and standard functions. For example, consider the function, f(x) = cos(x) + 5, the integral of this function is easy and can be easily calculated using the properties mentioned above. But now consider another function, f(x) = sin(3x + 5). This function is a composition of two different functions, the integral for this function is not as easy as the previous one. Such integrals are solved using the U-substitution method. 

∫f(g(x))g'(x)dx= ∫f(u)du

Here, u= g(x)  

Consider an example to understand the rule. 

f(x)= ∫2xcosx²dx  

Notice that the part cos(x²) is a composite function. 2x is the derivative of the inner part x². So, let’s say h(x) = x² and w(x) = cos(x). So, we can assume that u(x) = x² and w(x) = cos(x), 

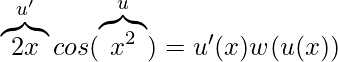
This is formulation of substitution. Consider u = x²

Thus, the function becomes, 

f(x) = ∫cosu du

This can be solved using standard formulas, 

f(x) = ∫cosu du = f(x) = sinu + C = f(x) = sinx² + C

Let’s see some problems on this rule, 

Sample Problems

Question 1: Find the integral of the following function f(x), 

f(x)= ∫10x(5x²)dx, 

Solution: 

Given f(x)= ∫10x(5x²)dx, 

Let F(x) be the integral of the function f(x), 

F(x)= ∫f(x)dx= F(x)= ∫10x(5x²)dx

Notice that the function is also a composite function, 

Let u = 5x². Differentiating the expression, 

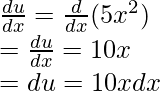
Using these results in the original integral equation, 

F(x)= ∫f(x)dx= F(x)= ∫udu

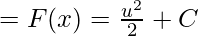
Substituting the value of “u” in the above equation, 

F(x) =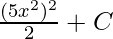 

Question 2: Find the integral of the following function f(x), 

 f(x) = 6x(3x²+ 5)

Solution: 

Given f(x) = 6x(3x²+ 5), 

Let F(x) be the integral of the function f(x), 

F(x)= ∫f(x)dx= F(x)= ∫F(x)= ∫6x(3x²+ 5) dx

Notice that the function is also a composite function, 

Let u = 3x² + 5. Differentiating the expression, 

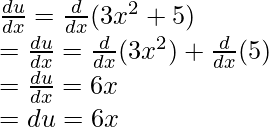
Using these results in the original integral equation, 

F(x)= ∫f(x)dx= F(x)= udu  

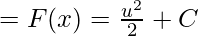
Substituting the value of “u” in the above equation, 

F(x) =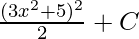 

Question 3: Find the integral of the following function f(x), 

 f(x)= ∫ (3x²+ 6x)(x³+ 3×2+ 5)

Solution: 

Given f(x)= ∫ (3x²+ 6x)(x³+ 3×2+ 5), 

Let F(x) be the integral of the function f(x), 

F(x)= ∫f(x)dx= F(x)= ∫ (3x²+ 6x)(x³+ 3×2+ 5) dx

Notice that the function is also a composite function, 

Let u = x³ + 3x² + 5. Differentiating the expression, 

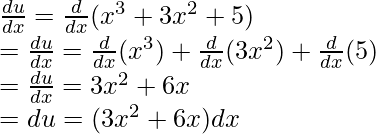
Using these results in the original integral equation, 

F(x)= ∫f(x)dx= F(x)= ∫udu

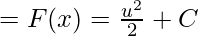
Substituting the value of “u” in the above equation, 

F(x) =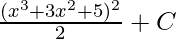 

Question 4: Find the integral of the following function f(x), 

f(x) = sin(x)cos(x)

Solution: 

Given f(x) = sinxcosx, 

Let F(x) be the integral of the function f(x), 

F(x)= ∫f(x)dx= F(x)= ∫ sinxcosxdx

Notice that the function is also a composite function, 

Let u = cos(x). Differentiating the expression, 

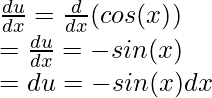
Using these results in the original integral equation, 

F(x)= ∫f(x)dx= F(x)= ∫ sin(x)cos(x)dx

F(x)= ∫-cos(x)(-sin(x))dx= F(x)= ∫-udu

Substituting the value of “u” in the above equation, 

F(x) = 

Question 5: Find the integral of the following function f(x), 

f(x)= ∫ 3x²cosx³

Solution: 

Given f(x)= ∫ 3x²cosx³, 

Let F(x) be the integral of the function f(x), 

F(x)= ∫f(x)dx= F(x)= ∫ 3x²cosx³dx

Notice that the function is also a composite function, 

Let u = x^3. Differentiating the expression, 

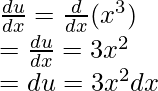
Using these results in the original integral equation, 

F(x)= ∫f(x)dx

F(x)= ∫3x2cos(x)dx

F(x)= ∫cosu du

F(x) = sinu +C

Substituting the value of “u” in the above equation, 

F(x) = sin(u) + C

⇒F(x) = sin(x³) + C

Question 6: Find the integral of the following function f(x), 

 f(x) = ∫3x²cosx³

Solution: 

Given f(x)= ∫3x²cosx³, 

Let F(x) be the integral of the function f(x), 

F(x)= ∫f(x)dx

F(x)= ∫3x²cosx³dx

Notice that the function is also a composite function, 

Let u = x^3. Differentiating the expression, 

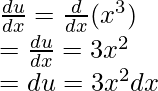
Using these results in the original integral equation, 

F(x)= ∫f(x)dx

F(x)= ∫3x²cos(x)dx

F(x)= ∫cosu du

F(x)= sin(u)+ C

Substituting the value of “u” in the above equation, 

F(x) = sin(u) + C

⇒F(x) = sin(x³) + C