Mathematics | Limits, Continuity and Differentiability
Last Updated :
27 Feb, 2024
1. Limits –
For a function
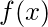
the limit of the function at a point
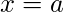
is the value the function achieves at a point which is very close to
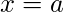
.
Formally,
Let
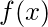
be a function defined over some interval containing
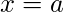
, except that it
may not be defined at that point.
We say that,
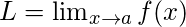
if there is a number

for every number

such that
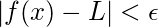
whenever
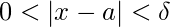
The concept of limit is explained graphically in the following image –
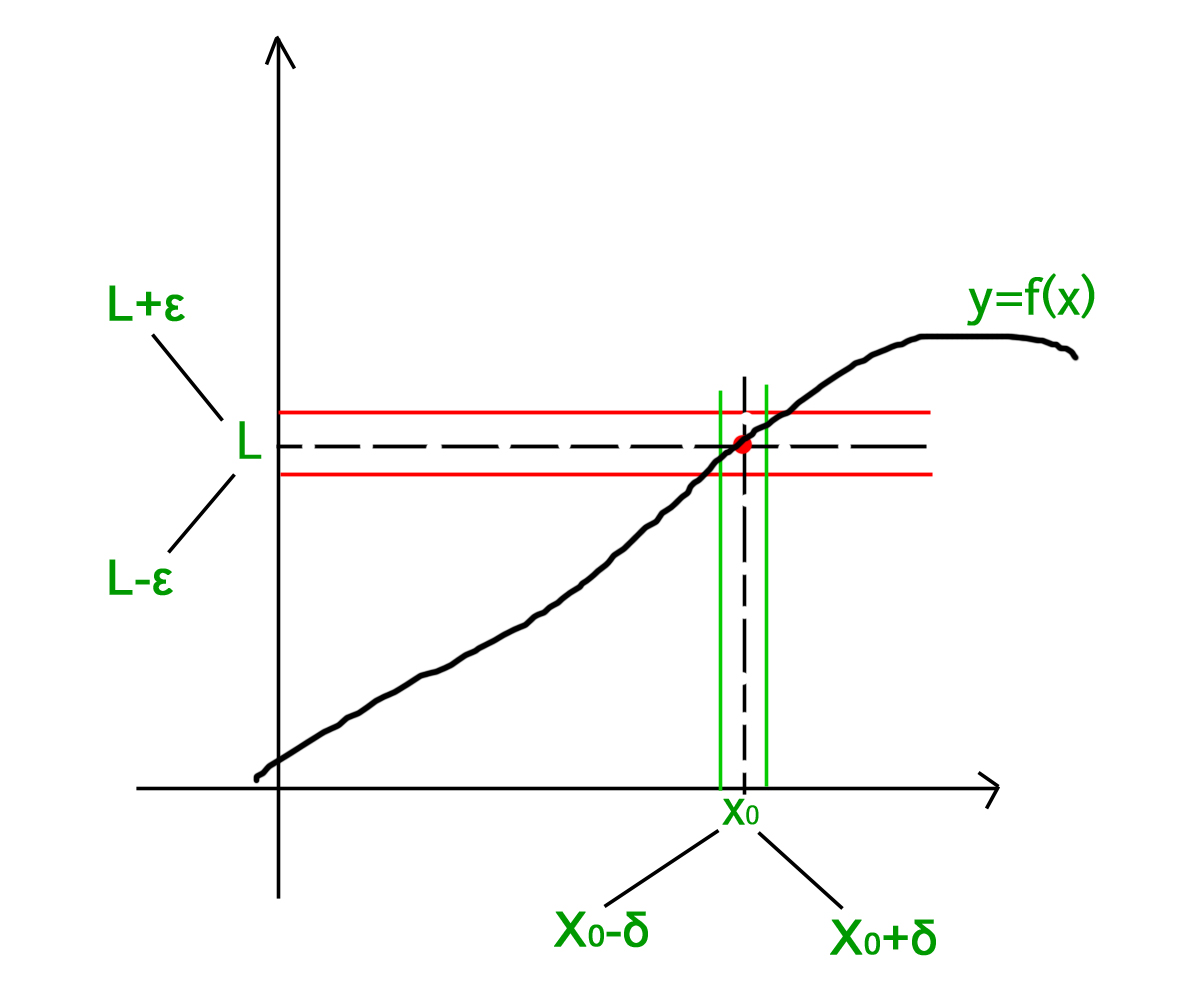
As is clear from the above figure, the limit can be approached from either sides of the number line i.e. the limit can be defined in terms of a number less that
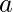
or in terms of a number greater than
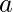
. Using this criteria there are two types of limits –
Left Hand Limit – If the limit is defined in terms of a number which is less than
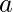
then the limit is said to be the left hand limit. It is denoted as
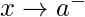
which is equivalent to
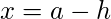
where

and
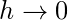
.
Right Hand Limit – If the limit is defined in terms of a number which is greater than
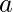
then the limit is said to be the right hand limit. It is denoted as
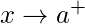
which is equivalent to
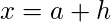
where

and
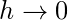
.
Existence of Limit – The limit of a function
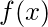
at
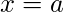
exists only when its left hand limit and right hand limit exist and are equal and have a finite value i.e.
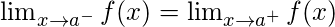
Some Common Limits –
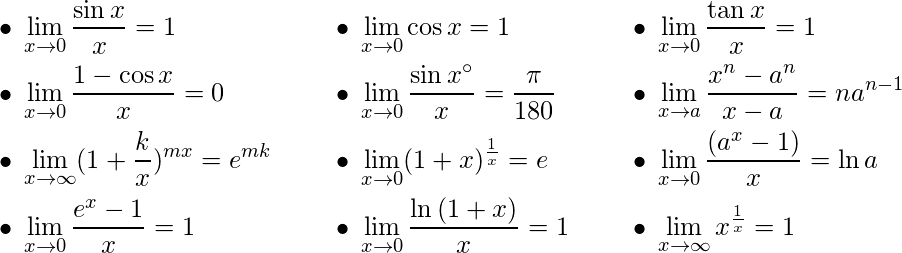
L’Hospital Rule –
If the given limit
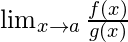
is of the form
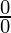
or
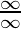
i.e. both
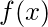
and
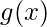
are 0 or both
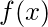
and
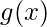
are
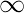
, then the limit can be solved by
L’Hospital Rule.
If the limit is of the form described above, then the L’Hospital Rule says that –
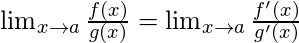
where
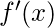
and
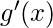
obtained by differentiating
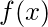
and
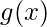
.
If after differentiating, the form still exists, then the rule can be applied continuously until the form is changed.
- Example 1 – Evaluate
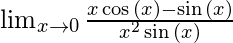
- Solution – The limit is of the form
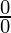 , Using L’Hospital Rule and differentiating numerator and denominator
, Using L’Hospital Rule and differentiating numerator and denominator
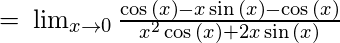
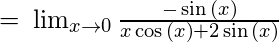
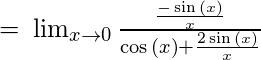
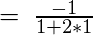
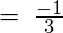
- Example 2 – Evaluate
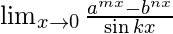
- Solution – On multiplying and dividing by
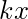 and re-writing the limit we get –
and re-writing the limit we get –
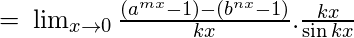
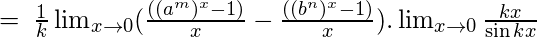
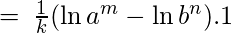
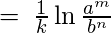
2. Continuity –
A function is said to be continuous over a range if it’s graph is a single unbroken curve.
Formally,
A real valued function 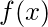 is said to be continuous at a point
is said to be continuous at a point 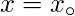 in the domain if –
in the domain if –
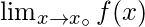 exists and is equal to
exists and is equal to 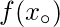 .
If a function
.
If a function 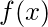 is continuous at
is continuous at 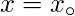 then-
then-
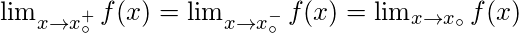 Functions that are not continuous are said to be discontinuous.
Functions that are not continuous are said to be discontinuous.
3. Differentiability –
The derivative of a real valued function 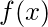 wrt
wrt 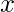 is the function
is the function 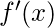 and is defined as –
and is defined as –
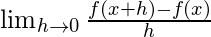 A function is said to be differentiable if the derivative of the function exists at all points of its domain. For checking the differentiability of a function at point
A function is said to be differentiable if the derivative of the function exists at all points of its domain. For checking the differentiability of a function at point 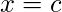 ,
,
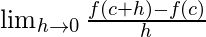 must exist.
If a function is differentiable at a point, then it is also continuous at that point.
Note – If a function is continuous at a point does not imply that the function is also differentiable at that point. For example,
must exist.
If a function is differentiable at a point, then it is also continuous at that point.
Note – If a function is continuous at a point does not imply that the function is also differentiable at that point. For example, 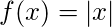 is continuous at
is continuous at 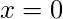 but it is not differentiable at that point.
but it is not differentiable at that point.
GATE CS Corner Questions
Practicing the following questions will help you test your knowledge. All questions have been asked in GATE in previous years or in GATE Mock Tests. It is highly recommended that you practice them.
1. GATE CS 2013, Question 22
2. GATE CS 2010, Question 5
3. GATE CS 2008, Question 1
4. GATE CS 2007, Question 1
5. GATE CS 2015 Set-1, Question 14
6. GATE CS 2015 Set-3, Question 19
7. GATE CS 2016 Set-1, Question 13
8. GATE CS 1998, Question 4
References-
Continuity – Wikipedia
Limits – Wikipedia
Differentiability – Wikipedia
Share your thoughts in the comments
Please Login to comment...