Discrete Random Variables are an essential concept in probability theory and statistics. Discrete Random Variables play a crucial role in modelling real-world phenomena, from the number of customers who visit a store each day to the number of defective items in a production line. Understanding discrete random variables is essential for making informed decisions in various fields, such as finance, engineering, and healthcare. In this article, we’ll delve into the fundamentals of discrete random variables, including their definition, probability mass function, expected value, and variance. By the end of this article, you’ll have a solid understanding of discrete random variables and how to use them to make better decisions.
Discrete Random Variable Definition
In probability theory, a discrete random variable is a type of random variable that can take on a finite or countable number of distinct values. These values are often represented by integers or whole numbers, other than this they can also be represented by other discrete values.
For example, the number of heads obtained after flipping a coin three times is a discrete random variable. The possible values of this variable are 0, 1, 2, or 3.
Examples of a Discrete Random Variable
A very basic and fundamental example that comes to mind when talking about discrete random variables is the rolling of an unbiased standard die. An unbiased standard die is a die that has six faces and equal chances of any face coming on top. Considering we perform this experiment, it is pretty clear that there are only six outcomes for our experiment. Thus, our random variable can take any of the following discrete values from 1 to 6. Mathematically the collection of values that a random variable takes is denoted as a set. In this case, let the random variable be X.
Thus, X = {1, 2, 3, 4, 5, 6}
Another popular example of a discrete random variable is the number of heads when tossing of two coins. In this case, the random variable X can take only one of the three choices i.e., 0, 1, and 2.
Other than these examples, there are various other examples of random discrete variables. Some of these are as follows:
- The number of cars that pass through a given intersection in an hour.
- The number of defective items in a shipment of goods.
- The number of people in a household.
- The number of accidents that occur at a given intersection in a week.
- The number of red balls drawn in a sample of 10 balls taken from a jar containing both red and blue balls.
- The number of goals scored in a soccer match.
Continuous Random Variable
Consider a generalized experiment rather than taking some particular experiment. Suppose that in your experiment, the outcome of this experiment can take values in some interval (a, b). That means that each and every single point in the interval can be taken up as the outcome values when you do the experiment. Hence, you do not have discrete values in this set of possible values but rather an interval.
Thus, X= {x: x belongs to (a, b)}
Example of a Continuous Random Variable
Some examples of Continuous Random Variable are:
- The height of an adult male or female.
- The weight of an object.
- The time is taken to complete a task.
- The temperature of a room.
- The speed of a vehicle on a highway.
Types of Discrete Random Variables
There are various types of Discrete Random Variables, some of which are as follows:
Binomial Random Variable
A binomial random variable is a type of discrete probability distribution that models the number of successes in a fixed number of independent trials, each with the same probability of success, denoted by p. It is named after the Swiss mathematician Jacob Bernoulli.
For example, the number of heads obtained when flipping a coin n times, or the number of defective items in a batch of n items can be modelled using a binomial distribution.
The probability mass function (PMF) of a binomial random variable X with parameters n and p is given by:
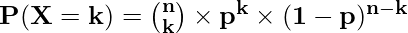
where k is a non-negative integer representing the number of successes in n trials.
The mean (expected value) and variance of a binomial random variable are given by:
E(X) = np
and
Var(X) = np(1-p)
Geometric Random Variable
A geometric random variable is a type of discrete probability distribution that models the number of trials required to obtain the first success in a sequence of independent Bernoulli trials, where each trial has a probability of success p and a probability of failure q = 1 – p.
For example, suppose you are flipping a fair coin until you get ahead. The number of times you flip the coin before obtaining a head is a geometric random variable. In this case, p = 0.5 because the probability of getting a head on any given flip is 0.5.
The probability mass function (PMF) of a geometric random variable is given by:
P(X=k) = (1-p)k-1× p
where X is the number of trials required to obtain the first success, and k is a positive integer representing the trial number.
The mean (expected value) and variance of a geometric random variable are given by:
E(X) = 1/p
and
Var(X) = (1-p)/p2
Bernoulli Random Variable
A Bernoulli random variable is a type of discrete probability distribution that models a single trial of an experiment with two possible outcomes: success with probability p and failure with probability q=1-p. It is named after the Swiss mathematician Jacob Bernoulli.
For example, flipping a coin and getting a head can be modelled as a Bernoulli random variable with p=0.5. Another example is the probability of a student passing a test, where the possible outcomes are passing with probability p and failing with probability q=1-p.
The probability mass function (PMF) of a Bernoulli random variable is given by:
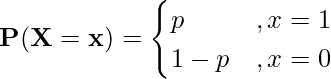
Where X is the random variable and 1 represents success and 0 represents failure.
The mean (expected value) and variance of a Bernoulli random variable are given by:
E(X) = p
and
Var(X) = p(1-p)
Poisson Random Variable
A Poisson random variable is a type of discrete probability distribution that models the number of occurrences of a rare event in a fixed interval of time or space. It is named after the French mathematician Siméon Denis Poisson.
For example, the number of phone calls received by a customer service centre in a given hour, the number of cars passing through a highway in a minute, or the number of typos in a book page can be modelled using a Poisson distribution.
The probability mass function (PMF) of a Poisson random variable X with parameter λ, where λ is the average number of occurrences per interval, is given by:
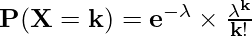
where k is a non-negative integer representing the number of occurrences in the interval.
The mean (expected value) and variance of a Poisson random variable are both equal to λ:
E(X) = λ
and
Var(X) = λ
Learn more about, Poisson Distribution
Difference Between Discrete Random Variable And Continuous Random Variable
The key differences between discrete and continuous random variables are as follows:
| | Discrete Random Variable | Continuous Random Variable |
|---|
| Definition | Takes on a finite or countably infinite set of possible values. | Takes on any value within a range or interval i.e., can be uncountably infinite as well. |
|---|
| Probability Distribution | Described by a probability mass function (PMF), which gives the probability of each possible value. | Described by a probability density function (PDF), which gives the probability density at each possible value. |
|---|
| Example | Number of heads in three coin tosses. | Height of a person selected at random. |
|---|
| Probability of a single value | Non-zero probability at each possible value. | Zero probability at each possible value. |
|---|
| Cumulative Distribution Function | Describes the probability of getting a value less than or equal to a particular value. | Describes the probability of getting a value less than or equal to a particular value. |
|---|
| Mean and Variance | Mean and variance can be calculated directly from the PMF. | Mean and variance can be calculated using the PDF and integration. |
|---|
| Probability of an Interval | The probability of an interval is the sum of the probabilities of each value in the interval. | The probability of an interval is the area under the PDF over the interval. |
|---|
Probability Distribution of Discrete Random Variable
A probability distribution is a way of distributing the probabilities of all the possible values that the random variable can take. Before constructing any probability distribution table for a random variable, the following conditions should hold a valid simultaneous when constructing any distribution table
- All the probabilities associated with each possible value of the random variable should be positive and between 0 and 1
- The sum of all the probabilities associated with every random variable should add up to 1
Example: Consider the following problem where a standard die is being rolled and it’s been given that the probability of any face is proportional to the square of the number obtained on its face. Obtain the probability distribution table associated with this experiment
Solution:
Since P(x) ∝ x => P(x) = kx2 where k is the proportionality constant and x are the numbers from 1 to 6
Also from the two conditions listed above we know that the sum of all probabilities is 1
Thus ∑ kx2 = 1 when summation is varied over x
⇒ k + 4k + 9k + 16k + 25k + 36k = 1
⇒ 91k =1
⇒ k = 1/91
Thus substituting this value of k into each probability we can obtain the probability of each random variable and then forming a table we get
| x | 1 | 2 | 3 | 4 | 5 | 6 |
|---|
| P(x) | 1/91 | 4/91 | 9/91 | 16/91 | 25/91 | 36/91 |
|---|
Checking the Validity of a Probability Distribution
Any valid probability distribution table should satisfy both the above-mentioned conditions namely
- All the probabilities associated with each possible value of the random variable should be positive and between 0 and 1
- The sum of all the probabilities associated with every random variable should add up to 1
Example: Check if the following probability distribution tables are valid or not
a)
This is a valid distribution table because
- All the individual probabilities are between 0 and 1
- The sum of all individual probabilities add up to 1
b)
| x | 0 | 1 | 2 | 3 | 4 | 5 |
|---|
| P(x) | 0.32 | 0.28 | 0.1 | -0.4 | 0.2 | 0.1 |
|---|
This is not a valid distribution table because
- There is one instance of a probability being negative
c)
This is not a valid distribution table because
- The sum of all the individual probabilities does not add up to 1 although they are positive and between 0 and 1. For a table to be a valid distribution table both conditions should satisfy simultaneously
Mean of Discrete Random Variable
We define the average of the random variable as the mean of the random variables. They are also called the expected value of the random variable. The formula and others for the same are discussed below in the article.
Expectation of Random Variable
An “expectation” or the “expected value” of a random variable is the value that you would expect the outcome of some experiment to be on average. The expectation is denoted by E(X).
The expectation of a random variable can be computed depending on the type of random variable you have.
For a Discrete Random Variable,
E(X) = ∑x × P(X = x)
For a Continuous Random Variable,
E(X) = ∫x × f(x)
Where,
- The limits of integration are –∞ to + ∞ and
- f(x) is the probability density function
Example: What is the expectation when a standard unbiased die is rolled?
Solution:
Rolling a fair die has 6 possible outcomes : 1, 2, 3, 4, 5, 6 each with an equal probability of 1/6
Let X indicate the outcome of the experiment
Thus P(X=1) = 1/6
⇒ P(X=2) = 1/6
⇒ P(X=3) = 1/6
⇒ P(X=4) = 1/6
⇒ P(X=5) = 1/6
⇒ P(X=6) = 1/6
Thus, E(X) = ∑ x × P(X=x)
⇒ E(X) = 1× (1/6) + 2 × (1/6) + 3 × (1/6) + 4 × (1/6) + 5 × (1/6) + 6 × (1/6)
⇒ E(X) = 7/2 = 3.5
This expected value kind of intuitively makes sense as well because 3.5 is in halfway in between the possible values the die can
take and thus this is the value that you could expect.
Properties of Expectation
Some properties of Expectation are as follows:
- In general, for any function f(x) , the expectation is E[f(x)] = ∑ f(x) × P(X = x)
- If k is a constant then E(k) = k
- If k is a constant and f(x) is a function of x then E[k f(x)] = k E[f(x)]
- Let c1 and c2 be constants and u1 and u2 are functions of x then E = c1E[u1(x)] + c2E[u2(x)]
Example: Given E(X) = 4 and E(X2) = 6 find out the value of E(3X2 – 4X + 2)
Solution:
Using the various properties of expectation listed above , we get
E(3X2 – 4X + 2) = 3 × E(X2) – 4 × E(X) + E(2)
= 3 × 6 – 4 × 4 + 2
= 4
Thus, E(3X2 – 4X + 2) = 4
Read More,
Variance and Standard Deviation of Discrete Random Variable
Variance and Standard deviation are the most prominent and commonly used measures of the spread of a random variable. In simple terms, the term spread indicates how far or close the value of a variable is from a point of reference. The variance of X is denoted by Var(X).
Standard Deviation is basically just the square root of the variance. i.e.,√Var(X).
Mathematically, for a discrete random variable X variance is given as follows:
Var(X) = E(X2) – [E(X)]2
and
S.D.(X) = √Var(X) = √[E(X2) – [E(X)]2 ]
Properties of Variance
Some properties of Variance are as follows:
- As Variance is a statistical measure of the variability or spread of a set of data, thus the variance of a constant is 0 i.e., Var(k) = 0 when k is a constant.
- If a random variable is changed linearly there is no effect of it on the variance i.e., Var[X+a] = Var[X].
- If a random variable is multiplied by some constant then Var[aX] = a2Var(X).
- Combining the above two properties to get, Var[aX + b] = a2Var(X)
Example 1: Find the variance and standard deviation when a fair die is rolled
Solution:
From one of the examples mentioned earlier , we figured out that the when a fair die is rolled, E(X) = 3.5
Also, to find out Variance, we would need to find E(X2)
Using properties of Expectation, E(X2) = ∑ x2 × P(X=x)
Thus, E(X2) = 1×(1/6) + 4×(1/6) + 9×(1/6) + 16×(1/6) + 25×(1/6) + 36×(1/6)
= 91/6 = 15.16
And Thus Var(X) = 15.16 – (3.5)2
= 2.916 = 35/12
Standard deviation is the square root of Variance
Thus, Standard deviation = 1.7076
Example 2: Find the variance and standard deviation of the following probability distribution table
Solution:
First off, we need to check if this distribution table is valid or not.
We see that both the conditions that are necessary for a distribution table being valid are satisfied simultaneously here. Thus, this is a valid distribution table.
Now to find variance, we need E(X) and E(X2)
E(X) = 0 × 0.1 + 1 × 0.2 + 2 × 0.4 + 3 × 0.3
Thus, E(X) = 1.9
E(X2) = 0 × 0.1 + 1 × 0.2 + 4 × 0.4 + 9 × 0.3
Thus, E(X2) = 4.5
Thus Var(X) = 4.5 – (1.9)2
= 0.89
Standard deviation = (0.89)0.5 = 0.9433
FAQs on Discrete Random Variable
Q1: What are Discrete Random Variables?
Answer:
A discrete random variable is a type of random variable that can only take on a finite or countably infinite number of values.
Q2: What is a Probability Distribution?
Answer:
A probability distribution is a function that describes the likelihood of different outcomes in a random event.
Q3: What is Expected Value?
Answer:
Expected values are the measure of the central tendency of a random variables which is nothing but the weighted average of the variables where probability is the weight. For discrete random variables expected value is given by
E(X) = ∑x × P(X = x)
Q4: What is Variance?
Answer:
Variance is a measure of the spread or dispersion of a random variable and is given by the formula
Var(X) = E(X2) – [E(X)]2
Q5: What is the Difference between Bernoulli Distribution and Binomial Distribution?
Answer:
A Bernoulli distribution is is a probability distribution for a single trial with only two possible outcomes (success or failure) whereas a binomial distribution is a probability distribution for the number of successes in a fixed number of independent Bernoulli trials.
Share your thoughts in the comments
Please Login to comment...