Product of Vectors
Last Updated :
05 Aug, 2021
Vector operations are used almost everywhere in the field of physics. Many times these operations include addition, subtraction, and multiplication. Addition and subtraction can be performed using the triangle law of vector addition. In the case of products, vector multiplication can be done in two ways either dot products or vector products. Vector products give vector as a resultant product after multiplication. In rotational motion, many quantities are derived using vector products. It becomes essential to understand the concepts and intuition behind this product. Let’s see this product in detail.
Product of Vectors
In the case of vector multiplication, there are basically two kinds of products- scalar and vector. The dot product is a kind of multiplication that results in a scalar quantity. Cross Product is a kind of multiplication that results in a vector quantity. Vector products are used to define other derived vector quantities. The equations for torque, angular velocity, and acceleration. All of these quantities involve the operations resulting in vectors from vectors. These operations are usually vector products.
Dot Product
Consider two vectors 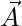 and
and 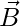 . The scalar product of these two vectors is defined by the equation,
. The scalar product of these two vectors is defined by the equation,
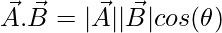
Here, θ is the angle between two vectors.

In case the vectors are given by their components. for example a = a1i + a2j + a3k and b = b1i + b2j + b3k. In this case, the dot product is given by,
a.b = a1b1i + a2b2j + a3b3k
Vector Product
Consider two vectors \vec{A} and \vec{B}. The vector product of these two vectors is denoted by  . The direction of this vector is perpendicular to both of the vectors. The magnitude of this vector is given by,
. The direction of this vector is perpendicular to both of the vectors. The magnitude of this vector is given by,
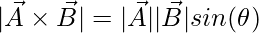
Here, θ is the angle between two vectors.

The right-hand rule is used to determine the direction of the resulting vector from the cross-product.
In case the vectors are given by their components. for example a = a1i + a2j + a3k and b = b1i + b2j + b3k. In this case, the cross product is given by,
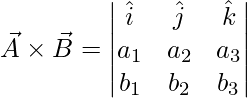
Property 1: Unlike the addition and dot product, the vector product is not commutative in nature.
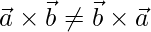
In this case, the magnitude of the both products will be same but the direction will be completely opposite. This means,
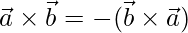
Property 2: The vectors products are distributive in nature with respect to vector addition. For example,
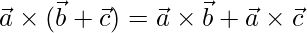
Sample Problems
Question 1: Two vectors are given by, a = 2i + j + k and b = i + j + k. Find the dot product of these two vectors.
Answer:
Given:
a = 2i + j + k
b = i + j + k
a.b
⇒ (2i + j + k ).( i + j + k )
⇒ 2.1 + 1.1 + 1.1
⇒ 4
Question 2: Two vectors are given by, a = i + j + k and b = i – 2j + 3k. Find the dot product of these two vectors.
Answer:
Given:
a = i + j + k
b = i -2j + 3k
a.b
⇒ (i + j + k ).( i – 2j + 3k )
⇒ 1.1 – 2.1 + 1.3
⇒ 1 – 2 + 3
⇒ 2
Question 3: Two vectors are given by, a = 4i +2 j +2 k and b = 2i + 2j + 2k. Find the cross product of these two vectors.
Answer:
Given:
a = 4i + 2j + 2k
b = 2i + 2j + 2k
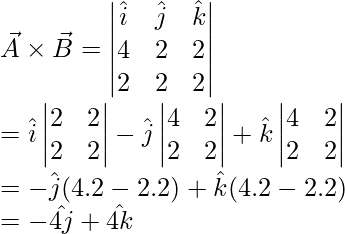
Question 4: Two vectors are given by, a = i – j + k and b = i – j + k. Find the cross-product of these two vectors.
Answer:
Given:
a = i – j + k
b = i – j + k
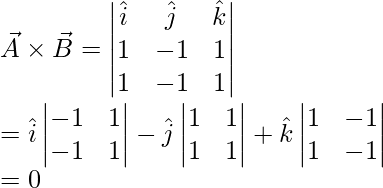
Question 5: Two vectors are given by, a = j + 4k and b = 5i +4j + 3k. Calculate c = a x b + b x a.
Answer:
Given:
a = j + 4k
b = 5i + 4j + 3k
Let the resultant vector be c,
c = a x b + b x a … (1)
As mentioned in the above properties, vector product in not commutative in nature.
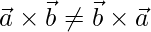
But this can be re-written,
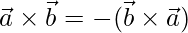
Using these values in the equation (1)
c = a x b + b x a
⇒ c = – (b x a) + b x a
⇒ c = 0
Question 6: Two vectors are given by, a = 2i + j + k and b = i + j + k. Find the cross product of these two vectors.
Answer:
Given:
a = 2i + j + k
b = i + j + k
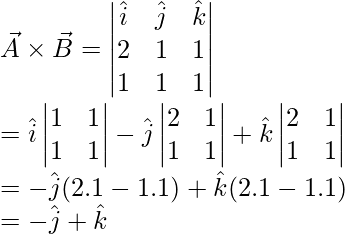
Share your thoughts in the comments
Please Login to comment...