A quantity that is characterized not only by magnitude but also by its direction, is called a vector. Velocity, force, acceleration, momentum, etc. are vectors.
Vectors can be multiplied in two ways:
- Scalar product or Dot product
- Vector Product or Cross product
Scalar Product/Dot Product of Vectors
The resultant scalar product/dot product of two vectors is always a scalar quantity. Consider two vectors a and b. The scalar product is calculated as the product of magnitudes of a, b, and cosine of the angle between these vectors.
Scalar product = |a||b| cos α
Here, |a| = magnitude of vector a |b| = magnitude of vector b α = angle between the vectors

Vectors a and b with angle α between them
Projection of one vector on other Vector
Vector a can be projected on the line l as shown below:

CD = projection of vector a on vector b
It is clear from the above figure that we can project one vector over another vector. AC is the magnitude of vector A. In the above figure, AD is drawn perpendicular to line l. CD represents the projection of vector a on vector b.
Triangle ACD is thus a right-angled triangle, and we can apply trigonometric formulae.
If α is the measure of angle ACD, then
cos α = CD/AC
Or, CD = AC cos α
From the figure, it is clear that CD is the projection of vector a on vector b
So, we can conclude that one vector can be projected over the other vector by the cosine of the angle between them.
Properties of Scalar Product
- Scalar product of two vectors is always a real number (scalar).
- Scalar product is commutative i.e. a.b =b.a= |a||b| cos α
- If α is 90° then Scalar product is zero as cos(90) = 0. So, the scalar product of unit vectors in x, y directions is 0.
- If α is 0° then the scalar product is the product of magnitudes of a and b |a||b|.
- Scalar product of a unit vector with itself is 1.
- Scalar product of a vector a with itself is |a|2
- If α is 1800, the scalar product for vectors a and b is -|a||b|
- Scalar product is distributive over addition
a.(b + c) = a.b + a.c
- For any scalar k and m then,
la.(m b) = km a.b
- If the component form of the vectors is given as:
a = a1x + a2y + a3z
b = b1x + b2y + b3z
then the scalar product is given as
a.b = a1b1 + a2b2 + a3b3
- The scalar product is zero in the following cases:
- The magnitude of vector a is zero
- The magnitude of vector b is zero
- Vectors a and b are perpendicular to each other
Inequalities Based on Dot Product
Cauchy – Schwartz inequality
According to this principle, for any two vectors a and b, the magnitude of the dot product is always less than or equal to the product of magnitudes of vector a and vector b
|a.b| ≤ |a| |b|
Proof:
Since, a.b = |a| |b| cos α
We know that 0 < cos α < 1
So, we conclude that |a.b| ≤ |a| |b|
Triangle Inequality
For any two vectors a and b, we always have
|a+ b| ≤ |a| + | b|

Triangle inequality
Proof:
|a+b|2=|a+b||a+b|
= a.a + a.b +b.a+ b.b
= |a|2+ 2a.b+|b|2 (dot product is commutative)
≤ |a|2 + 2|a||b| + |b|2
≤ (|a| + |b|)2
This proves that |a + b| ≤ |a| + |b|
Examples of Dot Product of Vectors
Example 1. Consider two vectors such that |a|=6 and |b|=3 and α = 60°. Find their dot product.
Solution:
a.b = |a| |b| cos α
So, a.b = 6.3.cos(60°)
=18(1/2)
a.b = 9
Example 2. Prove that the vectors a = 3i+j-4k and vector b = 8i-8j+4k are perpendicular.
Solution:
We know that the vectors are perpendicular if their dot product is zero
a.b = (3i+j-4k)( 8i-8j+4k)
= (3)(8) +(1)(-8)+(-4)(4)
=24-8-16 =0
Since the scalar product is zero, we can conclude that the vectors are perpendicular to each other.
Cross Product/Vector Product of Vectors
Readers are already familiar with a three-dimensional right-handed rectangular coordinate system. In this system, a counterclockwise rotation of the x-axis into the positive y-axis indicates that a right-handed (standard) screw would advance in the direction of the positive z-axis as shown in the figure.

3D Rectangular coordinate system
The vector product of two vectors a and b with an angle α between them is mathematically calculated as
a × b = |a| |b| sin α
It is to be noted that the cross product is a vector with a specified direction. The resultant is always perpendicular to both a and b.
In case a and b are parallel vectors, the resultant shall be zero as sin(0) = 0
Properties of Cross Product
- Cross Product generates a vector quantity. The resultant is always perpendicular to both a and b.
- Cross Product of parallel vectors/collinear vectors is zero as sin(0) = 0.
i × i = j × j = k × k = 0
- Cross product of two mutually perpendicular vectors with unit magnitude each is unity. (Since sin(0)=1)
- Cross product is not commutative.
a × b is not equal to b × a
- Cross product is distributive over addition
a × (b + c) = a × b+ a × c
k(a × b) = k(a) × b = a × k(b)
- On moving in a clockwise direction and taking the cross product of any two pair of the unit vectors we get the third one and in an anticlockwise direction, we get the negative resultant.

Cross product in clockwise and anticlockwise direction
The following results can be established:
i × j = k j × k = i k × i = j
j × i = -k i × k= -j k × j = -i
Cross product in Determinant Form
If the vector a is represented as a = a1x + a2y + a3z and vector b is represented as b = b1x + b2y + b3z
Then the cross product a × b can be computed using determinant form
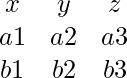
a × b = x(a2b3 – b2a3) + y(a3b1 – a1b3) + z(a1b2 – a2b1)
If a and b are the adjacent sides of the parallelogram OXYZ and α is the angle between the vectors a and b.
Then the area of the parallelogram is given by |a × b| = |a| |b|sin.α

Vectors a and b as adjacent sides of a parallelogram
Examples of Cross product of Vectors
Example 1. Find the cross product of two vectors a and b if their magnitudes are 5 and 10 respectively. Given that angle between then is 30°.
Solution:
a × b = a.b.sin (30) = (5) (10) (1/2) = 25 perpendicular to a and b
Example 2. Find the area of a parallelogram whose adjacent sides are
a = 4i+2j -3k
b= 2 i +j-4k
Solution:
The area is calculated by finding the cross product of adjacent sides
a × b = x(a2b3 – b2a3) + y(a3b1 – a1b3) + z(a1b2 – a2b1)
= i(-8+3) + j(-6+16) + k(4-4)
= -5i +10j
Therefore, the magnitude of area is 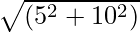
= 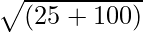
= 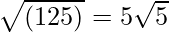
Application: Dot products and cross products are extensively useful for engineering applications.
Share your thoughts in the comments
Please Login to comment...