The word continuity means something which is continuous in nature. The flow of water is continuous, time in real life is continuous, and many more instances show the continuity in real life. In mathematics, the Continuous function is the one which when drawn on a graph does not show any breaks and is continuous in nature. Differentiability of function is possible only and only if it is continuous in nature. Logarithmic differentiation is a separate topic because of its multiple properties and for a better understanding of Log.
Continuity and Differentiability
Continuity of a function shows two things, the property of the function and the functional value of the function at any point. A function is said to be continuous at x = a, if its value remains same at x=a-, x=a+ and x=a. More formally, it can be written as,
A function is said to be continuous at in the closed interval [a, b], if
- f is continuous in (a, b)
- Follows

- Follows
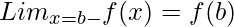
Differentiability means a function being differentiable, a function if said to be differentiable at x=a, it means that the f'(a) [the derivative of the function] exists at each and every point in that domain.
Differentiability⇢ 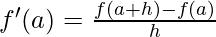
Logarithmic Differentiation
Logarithmic differentiation has its use in many places in physics and math, whether it comes to error solving or solving very complex functions, Logarithmic differentiation is preferred over simple differentiation. The method has properties and rules which when applied simplifies the calculation, applying the quotient rule and the product is not practical in very complex functions, at this point, going for logarithmic differentiation is a better choice.
Method of solving Logarithmic Differentiation
- First, Take the natural log on both sides of the equation given.
- Apply different properties of log to break the function and make it easier to solve.
- Differentiate the function applying rules, like chain rule.
- Multiply the RHS with the Function itself since it was in the denominator of the LHS.
Derivative of logₐx (for any positive base a≠1)
It is known that the differentiation of logx is 1/x, but this is the differentiation of natural log (that is, base e), is it possible to have different bases, and can their differentiation is possible as well? YES. With the help of 2 simple properties of log, it can be derived.
Let’s find out the derivative of Logax (where a is any positive integer a≠ 1),
d/dx(lnx)= 1/x
When the bases are changed, they can be written as,
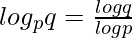
Therefore, to writing logax in the form given above and then differentiating it will give,
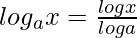
Differentiating both sides,
![Rendered by QuickLaTeX.com d/dx[log_ax]=d/dx[\frac{logx}{loga}]\\=\frac{1}{loga}d/dx[logx]\\=\frac{1}{xloga}](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-a5400032b7ee5bb2a411a4e36a68c418_l3.png)
Example 1: Find the differentiation for log9x
Answer:
d/dx[log9x]= d/dx[logx/log9]
![Rendered by QuickLaTeX.com d/dx[log_9x]=d/dx[\frac{logx}{log9}]\\=\frac{1}{log9}d/dx[logx]\\=\frac{1}{xlog9}](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-7855cfe82853ffba1db63d69f777d903_l3.png)
Example 2: Differentiate -5log6x
Answer:
![Rendered by QuickLaTeX.com d/dx[-5log_6x]=-5[d/dx[\frac{logx}{log6}]]\\=-5[\frac{1}{log6}d/dx[logx]]\\=\frac{-5}{xlog9}](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-decff17cf29ad3e7c45ad72b3d1a9f7c_l3.png)
Example 3: Differentiate log4(x2+x)
Solution:
As it is clear, that the function given is a Composite function. Therefore, chain rule is essential to be applied here.
y= log4(x2+x)
Assume x2+x be p(x)
p'(x)= 2x+1
For the log function, lets call it q(x)
q(x)= log4(x)
q'(x)=1/x.log4
y is the complete function which can now be written as,
y= q(p(x))
y’= q'(p(x))× p'(x)
dy/dx= 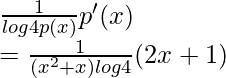
The above examples are related to the differentiation of logax and also the differentiation of composite numbers.
Some Basic properties of Log
| Property/Rule | Formula |
| Product | ln(xy)= ln(x)+ ln(y) |
| Log reciprocal | ln(1/x)= -ln(x) |
| Log of 1 | ln(1)= 0 |
| Log of e | ln(e)= 1 |
| Log of power | ln(x)y= yln(x) |
| Quotient | ln(x/y)= ln(x)-ln(y) |
Now lets take a look at some other examples based on the properties of logarithm.
Sample Problems
Question 1: Differentiate, 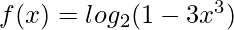
Solution:
Differentiating, 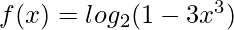
Assume, 1-3x3= v(x)
Where, v(x) is also a function of x, hence it is needed to be differentiated as well.
![Rendered by QuickLaTeX.com d/dx[f(x)]=d/dx[ log_2{(1-3x^3)}]\\=d/dx[ log_2{(v(x))}] \\=\frac{v'(x)}{log2{(v(x))}}\\= \frac{-9x^2}{log2(1-3x^3)}](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-327bf88eba4af65c91eb3fea6e37b7fd_l3.png)
Question 2: Differentiate, h(x)= 5ln(x)
Solution:
d/dx[ln(x)]= 1/(x)
Hence, d/dx[h(x)] = h'(x)= d/dx[5/x]
h'(x)= 5/x
Question 3: Differentiate, y= ln(4+ 7x5)
Solution:
y’= d[y]/dx =d/dx[ln(4+7x5)]
dy/dx= ![Rendered by QuickLaTeX.com \frac{d/dx[4+7x^5]}{4+7x^5}\\=\frac{35x^4}{4+7x^5}](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-8836b2c2b2a3ae41a2d951007bbe7f4b_l3.png)
Question 4: Differentiate, y = cosx × cos3x × cos5x
Solution:
Add log on both sides,
Logy= log{cosx × cos3x × cos5x}
Logy= log(cosx) × log(cos3x) × log(cos5x)
Differentiating on both sides,
d/dx[logy]= d/dx[log(cosx) × log(cos3x) × log(cos5x)]
1/y × dy/dx = [(1/cosx) × d(cosx)/dx] + [1/cos3x × d(cos3x)/dx] + [1/cos5x × d(cos5x)/dx]
1/y × dy/dx = -sinx/cosx -3sin3x/cos3x -5 sin5x/cos5x
dy/dx= y × {-tanx-3tan3x-5tan5x}
dy/dx= {cosx× cos3x × cos5x} × {-tanx -3tan3x -5tan5x}
Question 5: What is the meaning of Log of a number?
Answer:
A Log or Logarithms is the power to which a number must be raised in order to get another number. For example, the logarithm of base 10 for 1000 is 3, the base 10 logarithms of 10000 is 4, and so on. Log is used to find the skewness in large values and to show percent change of multiple factors.
Question 6: Differentiate, 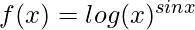
Answer:

Add Log both sides,
Logy= (Sinx)Log{log(x)}
Differentiate with respect to x on both sides,
1/y dy/dx= 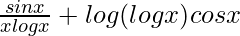
dy/dx= y × 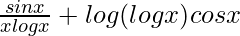
dy/dx= logxsinx![Rendered by QuickLaTeX.com [\frac{sinx}{xlogx}+{log(logx)}cosx]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-584fc77d568c9fc6162a5197a3488f74_l3.png)
Question 7: Explain in steps to solve the Logarithmic Differentiation.
Answer:
Steps to solve logarithmic differentiation are very easy and short,
- Take Log on both sides of the equation
- Use the properties of Log and simplify RHS
- Differentiate both sides, apply chain rule on RHS
- Put the value of the function both sides
Question 8 : Differentiate, 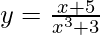
Answer:
Apply log on both sides,
![Rendered by QuickLaTeX.com Logy= Log[\frac{x+5}{x^3+3}]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-ee27c7030183796573de5be1f339a196_l3.png)
1/y. dy/dx= d/dx {log(x+5) -log(x3+ 3)}
1/y. dy/dx = 1/(x+5) – 3x/(x3+3)
dy/dx= y [1/(x+5) – 3x/(x3+3)]
dy/dx= ![Rendered by QuickLaTeX.com \frac{x+5}{x^3+3}[\frac{1}{x+5}-\frac{3x}{x^3+3}]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-18d763f8b76badc4ca6a12728ff40853_l3.png)
Question 9: Differentiate, 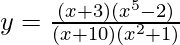
Answer:
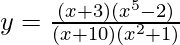
Taking Log on both sides,
![Rendered by QuickLaTeX.com logy=log [\frac{(x+3)(x^5-2)}{(x+10)(x^2+1)}]\\=log(x+3)+log(x^5-2)-log(x+10)-log(x^2+1) \\\frac{dy}{dx}\frac{1}{y}=\frac{1}{x+3}+\frac{5x^4}{x^5-2}-\frac{1}{x+10}-\frac{2x}{x^2+1} \\dy/dx=y[\frac{1}{x+3}+\frac{5x^4}{x^5-2}-\frac{1}{x+10}-\frac{2x}{x^2+1}] \\dy/dx= [\frac{(x+3)(x^5-2)}{(x+10)(x^2+1)}][\frac{1}{x+3}+\frac{5x^4}{x^5-2}-\frac{1}{x+10}-\frac{2x}{x^2+1}]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-d0ac90f8ee22968cf6823ca7d280763d_l3.png)
Like Article
Suggest improvement
Share your thoughts in the comments
Please Login to comment...