Physical quantities are divided into two categories – scalar and vector quantities. The quantities which have only magnitude and not any fixed direction are called Scalar quantities. Eg. Mass, volume, density, etc. Quantities that have both magnitude and direction. Such quantities are called vector quantities or vectors. Eg. Displacement, velocity, acceleration, momentum, etc.
Vectors are represented by line segments that are directed such as, the direction of an arrow marked at one end, which denotes direction and the length of the line segment is the magnitude of the vector. Eg. 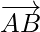
It denotes two points A and B, such that the magnitude of the vector is the length of the straight line AB and its direction is from A to B. Here, point A is called the initial point of vector 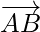 and point B is called the terminal point(or endpoint).
and point B is called the terminal point(or endpoint).
The magnitude or modulus of a vector \overrightarrow{AB} is a positive number(>0) which is the measure of its length and is denoted by |\overrightarrow{AB}|.

Types of Vectors
Zero Vector
A vector whose initial and terminal(end) points coincide with each other, is called a zero vector (or null vector), and denoted as 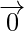 . Zero vector can not be assigned a defined direction as it has zero magnitude. Or, in other words, it may be defined as having any direction.
. Zero vector can not be assigned a defined direction as it has zero magnitude. Or, in other words, it may be defined as having any direction.
The vectors 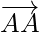 ,
, 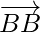 represent the zero vector.
represent the zero vector.
Unit Vector
A vector whose magnitude is unity (=1) is called as unit vector. The unit vector 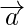 is denoted by
is denoted by 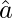
and 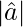 = 1
= 1

Coinitial Vectors
Two or more vectors having the same initial point or starting point are called coinitial vectors.
Collinear Vectors
If two or more vectors are parallel to each other, irrespective of their magnitudes and directions. Then they will be called collinear vectors.
Equal Vectors
If two vectors 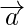 and
and 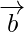 have the same magnitude and direction regardless of the positions of their initial points will be called as equal vectors, and it can be represented as
have the same magnitude and direction regardless of the positions of their initial points will be called as equal vectors, and it can be represented as 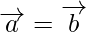
Negative of a Vector
A vector whose magnitude(length) is equal to of given vector (say 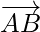 ) but the direction is opposite to that of it(initial and terminal points are reversed), is called negative of the given vector.
) but the direction is opposite to that of it(initial and terminal points are reversed), is called negative of the given vector.
For example, vector 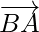 is negative of the vector
is negative of the vector 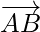 and written as,
and written as, 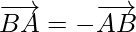
Position Vector
Consider a point P in 3D space, having coordinates as (x, y, z) with respect to the origin O(0, 0, 0). And, the vector 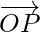 is having O as the initial point and P as its terminal point is called the position vector of the point P with respect to O.
is having O as the initial point and P as its terminal point is called the position vector of the point P with respect to O.

Using the distance formula, the magnitude(or length) of 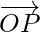 is
is
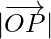 =
= 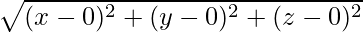
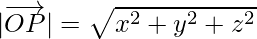
Note: The vector’s definition defined above are such type of vectors that can be subjected to its parallel displacement without changing its magnitude and direction. Such vectors are called free vectors.
Vector Addition
A vector 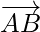 simply denotes the displacement of anything from point A to point B.
simply denotes the displacement of anything from point A to point B.
Triangle law of vector addition
Consider a situation that a person moves from A to B and then from B to C. The net displacement made by the person from point A to point C, is given by the vector and expressed as

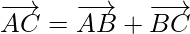
This is known as the triangle law of vector addition.
As, 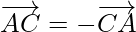
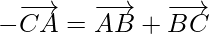
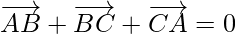
When the sides of a triangle are taken in order, then it leads to zero resultant(no displacement result) as the initial and terminal points get coincided with each other.
Parallelogram Law of Vector Addition
If two vectors 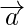 and
and 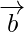 are represented in magnitude and direction by the two adjacent sides of the parallelogram, then their sum(
are represented in magnitude and direction by the two adjacent sides of the parallelogram, then their sum(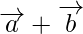 )
) 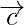 is represented by the diagonals of the given parallelogram which is coinitial with the given vectors
is represented by the diagonals of the given parallelogram which is coinitial with the given vectors 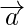 and
and 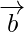 .
.
Now, let’s consider the parallelogram ABCD

where, 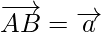 and
and 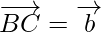
then by using the triangle law of vector addition, from triangle ABC, we have
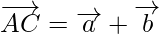 ………………….(1)
………………….(1)
Now, as the opposite sides of a parallelogram are equal and parallel
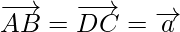 and
and 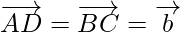
Again using triangle law of vector addition, from triangle ADC, we have
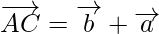 …………………………….(2)
…………………………….(2)
From (1) and (2), we get commutative property
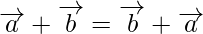
Note: The magnitude 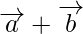 is not equal to the sum of the magnitude(length) of
is not equal to the sum of the magnitude(length) of 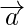 and
and 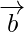 .
.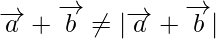
(ii) Associative property

Using triangle law, from triangle PQR, we have
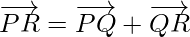
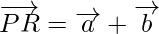
Using triangle law, from triangle QRS, we have
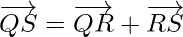
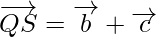
Using triangle law, from triangle PRS, we have
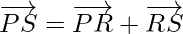
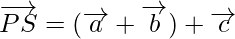
Using triangle law, from triangle PQS, we have
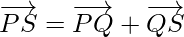
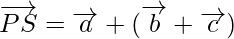
Hence,
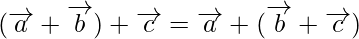
(iii) Additive identity
For any vector 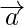
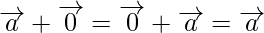
(iv) Additive inverse
For any vector 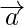
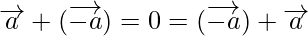
Problem 1: If 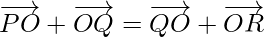 , show that the points P, Q and R are collinear.
, show that the points P, Q and R are collinear.
Solution:
We have,
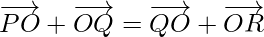
Using, converse of triangle law of addition of vectors, we get
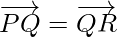
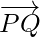 and
and 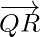 ae either parallel or collinear. But, Q is a point common to them.
ae either parallel or collinear. But, Q is a point common to them.
So, 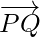 and
and 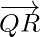 are collinear. Hence, points P, Q, R are collinear.
are collinear. Hence, points P, Q, R are collinear.
Problem 2: B, P, Q, R and A are five points in a plane. Show that the sum of vectors 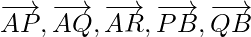 and
and 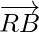 in 3
in 3 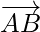 .
.
Solution:

Using triangle law addition of vectors in △APB
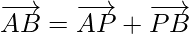 ……………(1)
……………(1)
Using triangle law addition of vectors in △AQB
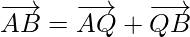 …………………..(2)
…………………..(2)
Using triangle law addition of vectors in △ARB
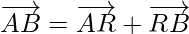 …………….(3)
…………….(3)
Adding (1), (2) and (3), we get
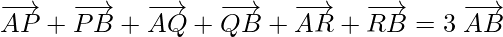
Hence, the sum of the vectors is 3 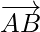
Problem 3: Let O be the centre of a regular hexagon CDEFAB. Find the sum of the vectors 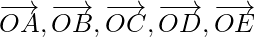 and
and 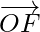 .
.
Solution:

As hexagon property states that, the centre of a regular hexagon bisects all the diagonals passing through it.
So,
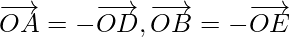 and
and 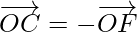
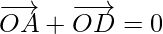 ………………..(1)
………………..(1)
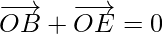 …………………..(2)
…………………..(2)
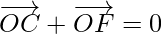 …………………..(3)
…………………..(3)
By adding (1), (2) and (3), we get
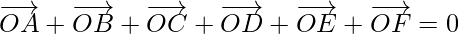
Section formula
Here, the points P and Q are the two points represented by the position vectors 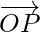 and
and 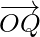 , respectively, with respect to the origin O. Then the line segment joining the points P and Q can be divided by a third point, here we say R, in two ways as follows:
, respectively, with respect to the origin O. Then the line segment joining the points P and Q can be divided by a third point, here we say R, in two ways as follows:
Here, we intend to find the position vector 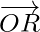 for the point R with respect to the origin O. We take the two cases one by one.
for the point R with respect to the origin O. We take the two cases one by one.
Internally

When R divides PQ internally. If R divides 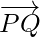 such that
such that
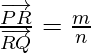
where m and n are positive values, we specify that the point R divides 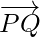 internally in the ratio of m : n.
internally in the ratio of m : n.
Now from triangles ORQ and OPR, we have
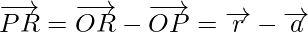
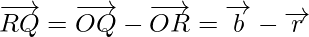
Hence, we can conclude that,
m 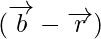 = n
= n 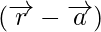
On simplification, we get
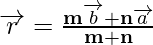
When R is the midpoint PQ
then m = n
So, we get
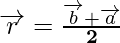
Externally

When R divides PQ externally. If R divides 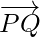 such that
such that
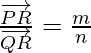
where m and n are positive values, we say that the point R divides 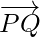 externally in the ratio of the m : n.
externally in the ratio of the m : n.
Now from triangles ORQ and OPR, we have
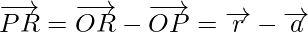
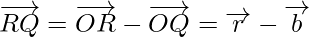
Hence, we can conclude that,
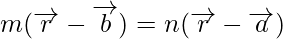
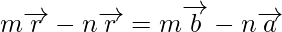
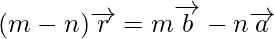
On simplification, we get
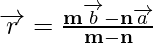
Problem 1: Find the position vectors of the points which divide the join of the points 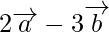 and
and 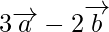 internally and externally in the ratio 2 : 3.
internally and externally in the ratio 2 : 3.
Solution:
Let A and B be the given points with the position vectors 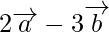 and
and 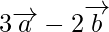 respectively.
respectively.
Let P divide the 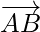 in the ratio 2 : 3 internally
in the ratio 2 : 3 internally
m = 2 and n = 3
Using internally section formula,

Position vector of P = 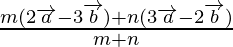
Position vector of P = 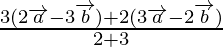
Position vector of P = 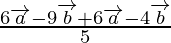
Position vector of P = 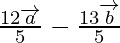
Now, Let P divide the 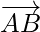 in the ratio 2 : 3 externally
in the ratio 2 : 3 externally
m = 2 and n = 3
Using externally section formula,

Position vector of P = 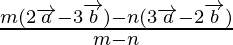
Position vector of P = 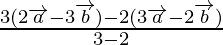
Position vector of P = 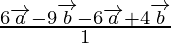
Position vector of P = 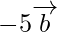
Problem 2: If 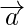 and
and 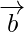 are position vectors of points A and B respectively, then find the position vector of points of trisection of AB.
are position vectors of points A and B respectively, then find the position vector of points of trisection of AB.
Solution:
Let P and Q be points of trisection. Then, AP = PQ = QB = k (constant variable)
PB = PQ + QB = k + k = 2k
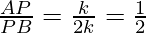
P divides AB in the ratio 1 : 2

Using internally section formula, where m=1 and n=2
Position vector of P = 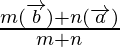
Position vector of P = 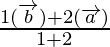
Position vector of P = 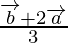
Now, we can clearly see that Q is the mid-point of PB.
Apply mid-point section formula we have,
Position vector of Q = 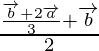
Position vector of Q = 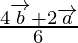
Position vector of Q = 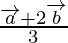
Problem 3: If D is the mid-point of the side BC of a triangle ABC, prove that 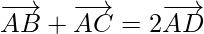
Solution:
Let A be the origin here and position vectors of B and C be 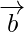 and
and 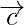 respectively.
respectively.

As D is the mid-point of BC.
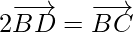
Applying mid-point section formula, we get
Position vector of D = 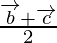
As, 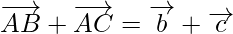
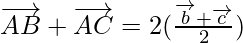
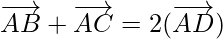
Hence, Proved!!
Components of a vector
Let’s take the points A(1, 0, 0), B(0, 1, 0) and C(0, 0, 1) on the x-axis, y-axis and z-axis, respectively. Then,

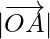 = 1,
= 1, 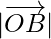 = 1 and
= 1 and 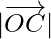 = 1
= 1
The vectors, 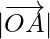 ,
, 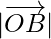 and
and 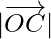 are having magnitude unity or 1, which are called unit vectors along the axes OX, OY and OZ, respectively, and denoted by
are having magnitude unity or 1, which are called unit vectors along the axes OX, OY and OZ, respectively, and denoted by 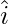 ,
, 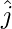 and
and 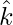 respectively.
respectively.
Lets, consider the position vector 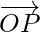 , of a point P(x, y, z). Let P1 be the foot of the perpendicular from P on the XY plane.
, of a point P(x, y, z). Let P1 be the foot of the perpendicular from P on the XY plane.

Hence we see that P1P is parallel to z-axis. As 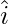 ,
, 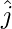 and
and 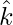 are the unit vectors along the axes x, y and z, respectively, and by the definition of the coordinates of P, we have
are the unit vectors along the axes x, y and z, respectively, and by the definition of the coordinates of P, we have
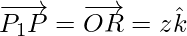
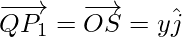
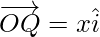
Using triangle law, from triangle OQP1, we have
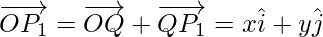
Using triangle law, from triangle OP1P, we have
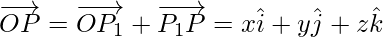
Hence, the position vector of P with reference to O is as follows:
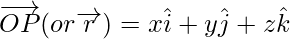
Length
The length of vector 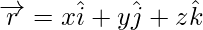 ,
,
OP12 = OQ2 + QP12 (Using Pythagoras theorem)
OP12 = x2 + y2
and in the right-angled triangle OP1 P, we have
OP2 = OP12 + PP12
OP2 = x2 + y2 + z2
OP = 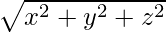
Hence, the length of vector 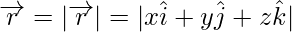
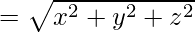
If 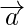 and
and 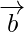 are two vectors as
are two vectors as 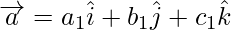 and
and 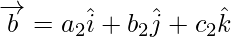 then,
then,
Sum
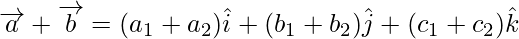
Difference
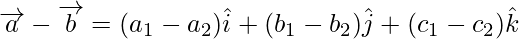
The vectors 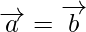 , iff
, iff
a1 = a2, b1 = b2 and c1 = c2
The multiplication of vector by any scalar k is given by
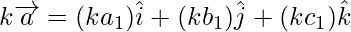
Vector joining two points
If P(x1, y1, z1) and Q(x2, y2, z2) are any two points, then the vector joining P and Q is the vector 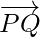
Joining the points P and Q with the origin O, and applying triangle law, from the triangle OPQ, we have

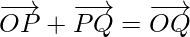
Using the properties of vector addition, the above equation become
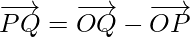
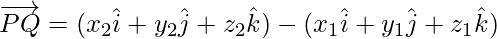
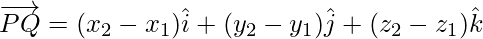
Hence, the magnitude of  is as follows:
is as follows:
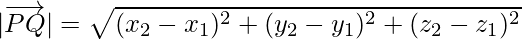
Problem 1: Find the value of x, y and z so that the vectors 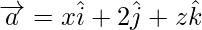 and
and 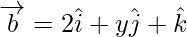 are equal.
are equal.
Solution:
Two vectors 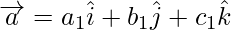 and
and 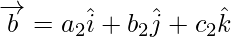 are equal iff
are equal iff
a1 = a2 , b1 = b2 and c1 = c2
Hence, the values of x = 2, y = 2 and z =1.
Problem 2: Find the magnitude of the vector 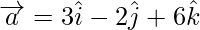
Solution:
As, we have 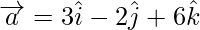
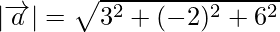
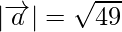 = 7
= 7
Problem 3: Find the unit vector of given vector as 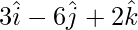
Solution:
Let, 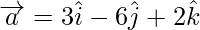
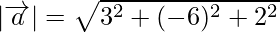
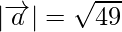 = 7
= 7
So, the unit vector in the direction of 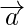 is given by,
is given by,

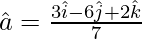
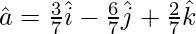
Problem 4: Find the unit vector of given vector as 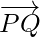 , where the points P(1,2,3) and Q(4,5,6).
, where the points P(1,2,3) and Q(4,5,6).
Solution:
Position vector of P(1,2,3) = 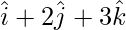
Position vector of Q(4,5,6) = 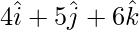
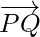 =
= 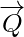 –
– 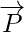
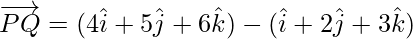
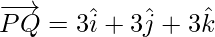
Now, magnitude of 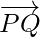
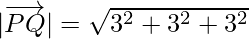
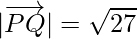 = 3√3
= 3√3
So, the unit vector in the direction of 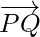 is given by,
is given by,
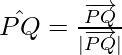
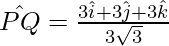
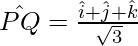
Problem 5: Show that the vector 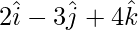 and
and 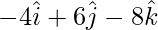 are collinear.
are collinear.
Solution:
Let, 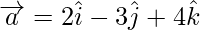 and
and 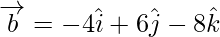
As, we can see
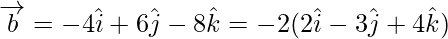
This implies,
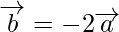
Hence, 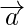 and
and 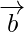 are collinear.
are collinear.
Problem 6: If A(2,0,0), B(0,1,0), C (0,0,2) have position vectors, show that △ABC is isosceles triangle.
Solution:

Position vector of A(2,0,0) = 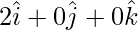
Position vector of B(0,1,0) = 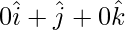
Position vector of C(0,0,2) = 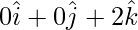
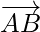 =
= 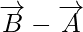
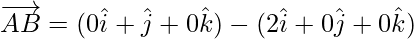

Now, magnitude of 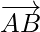
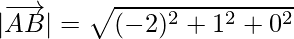
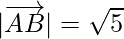
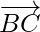 =
= 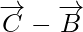
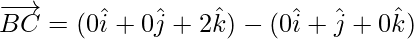
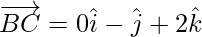
Now, magnitude of 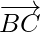
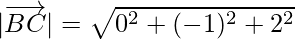
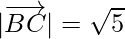
Clearly, AB = BC.
Hence, △ABC is isosceles triangle.
Like Article
Suggest improvement
Share your thoughts in the comments
Please Login to comment...