Relative maxima and minima are the points defined in any function such that at these points the value of the function is either maximum or minimum in their neighborhood. Relative maxima and minima depend on their neighborhood point and are calculated accordingly. We find the relative maxima and minima of any function by using the first derivative test and the second derivative test.
In this article, we have covered Relative Maxima and Minima, methods to find relative maxima and minima, various examples, and others in detail. Before starting with Relative Maxima and Minima, first, learn in brief about Maxima and Minima.
What is Maxima and Minima?
Maxima and Minima are called critical points of the function. A maxima is a high point and a minima is a low point in any function. In a function, more than one maximum and minimum point can exist. The points at which the function attains the highest and lowest values are called Maxima and Minima.
What Is Relative Maxima and Minima?
Relative maxima and minima are the points at which the function gives the maximum and minimum values respectively in their neighborhood. Relative maxima and minima of any function are easily found by using the first derivatives and second derivative test respectively. The graph added below the relative maxima and minima of a function in its neighborhood.

How to Find Points of Maxima and Minima? (First Derivative Test)
In any smoothly changing function, the points where the function flattens out, give us either minima or maxima. Now, this statement gives rise to two questions.
- How to recognize the points at which function flattens out?
- Suppose we got a point at which function flattens i.eofcritical point. How to tell whether it’s a minimum or a maximum?
To answer the first question let’s look at the slope of the function. The points where the function flattens out have zero slopes. We know that the derivative is nothing but the slope of the function at a particular point. So, we try to find the points where the derivative is zero. Thus, this test is also called the First Derivative Test. Then we equate the differential equation with zero to get the critical points as,
f'(x) = 0
The solution to this equation gives us the position of the critical points. These critical points tells us that these are the points where the tangent to the curve is parallel to x-axis but still we don’t know whether they are points o maxima or minima for that Second Derivative test is used.
Recognizing Maxima and Minima
As shown in the figure below, it can be seen that if the sign of the derivative is positive before the critical point and negative after the critical point, it is a maximum. Similarly, if it is negative before the critical point and positive after the critical point. It is a minimum. Maxima and minima can also be recognized by the second derivative test.

Notice the figure carefully, and see that the slope of the curve is continuously decreasing, and then it becomes zero and goes further towards a negative value.
Second Derivative Test
When a function’s slope is zero at x, then the second derivative f”(x) at that point is used to tell whether at that point we have maxima or minima.
- f”(x) < 0, if it is a maxima.
- f”(x) > 0, if it is a minima.
Note: If the second derivative is zero at the critical points, then the test fails.
Steps to Find Relative Maxima and Minima
To find the relative maxima and minima of a function follow the steps added below, suppose we are given a function,
f(x) = x2 – 4
and we have to find its maximum and minimum value in the interval [-2, 2] then,
Step 1: Differentiate the Function
Given,
f'(x) = 2x
Step 2: Find out Critical Points
Putting f'(x) = 0 gives us the position of the critical points for the function. For the given function,
2x = 0
⇒ x = 0
Thus, x = 0 is a critical point for this function. Now we need to find out whether it is a minimum or a maximum.
Step 3: Second Derivative Test
We use the second derivative test mentioned above to find out whether the given critical point is minima or maxima. In the above case,
f”(x) = 2
Notice that, f”(x) > 0. Thus, it must be a minimum.
Step 4: Value at Critical Points
Find the value of the function at critical points get the smallest value(or the minima)
Thus, the minimum value of f(x) is at x = 0 and the minimum value is -4.
Applications of Relative Maxima and Minima
Relative Maxima and Minima has various applications. it is used for various purposes such as,
- This concept is used to determine the maximum and minum value of a stock at particular points by equating it to a function that represent the trajectory of the stocks.
- This concept are used in electronic circuits to manage the voltage and current in the system.
- Relative maxima and minima is also used in astrophyscis to find the maximum and minimum trajectory of an abject, etc.
Read More,
Examples on Relative Maxima and Minima
Example 1: Find all the critical points of the following function,
f(x) = x3 – 6x2 +11x – 6
Solution:
Given Function,
f'(x) = 3x2 -12x +11 = 0
⇒ 3x2 -12x +11 = 0
Using Quadratic Formula,
x = 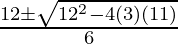
x = 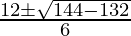
x = 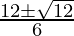
x = 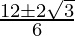
Thus, the critical points of the given function are,
x = 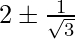
Example 2: Find the relative minima of the function, f(x) = x2 – 4x + 4.
Solution:
Given function,
f'(x) = 2x – 4 = 0
⇒x = 2
Using Second Derivative test,
f”(x) = x
at x = 2
f”(x) = 2 > 0
Thus, at x = 2 is a minima and the minimum value of function is,
f(2) = (2)2 -4(2) + 4 = 4 – 8 + 4 = 0 (Minimum Value)
Example 3: Find the relative maxima and minima of, f(x) =x2 -7x + 12.
Solution:
Given function,
For finding the critical point of the function,
f'(x) = 2x – 7 = 0
⇒ x = 7/2
Using second derivative test,
f”(x) = x
at x = 7/2
f”(7/2) = 7/2 > 0 (Point of Minima)
Thus, the value of function is minimum at point x = 7/2 and its minimum value is,
f(7/2) = (7/2)2 – 7(7/2) + 12 = -1/4
Example 4: Find relative maxima and minima of, f(x) =ex + e-x.
Solution:
Given function,
Finding the critical points,
f'(x) = ex – e-x = 0
⇒ ex = e-x
Taking log both sides,
⇒ x = -x
⇒x = 0
Thus, x = 0 is a critical point.
Using Second Derivative Test,
f”(x) = ex + e-x
At, x = 0
f”(2) = 2 > 0 (Point of Minima)
Finding minimum value of the function,
f(0) = e(0) + e(0) = 1 + 1 = 2
FAQs on Relative Maxima and Minima
1. What is Relative Maxima and Minima of Fucntion?
Relative maxima or minima is the maximum or minmun value of the function for given set of points.
2. What is Difference Between Relative Maxima and Absolute Maxima?
Relative maxima or minima is the maximum or minmun value of the function for given set of points whereas, absolute maxima or minima is the maximum or minimum value of the function for the entire domian.
3. How to Find Relative Maxima and Minima of Fucntion?
Relative maxima and mimima of the function is found using the steps added below,
Step 1: Find the derivative of the function.
Step 2: Equate the derivative value of the function with zero and get the critical value of the function.
Step 3: Use the second derivative test to check wether we have maxima or minima at critical points.
Step 4: Find the maximum or minimum value of function at critical points.
4. What are the Uses of Relative Maxima and Minima?
Relative Maxima and Minima is used to find the maximum or minimum value of the function for the given set of points.
Like Article
Suggest improvement
Share your thoughts in the comments
Please Login to comment...