Differential Equations are used to describe a lot of physical phenomenons. They help us to observe something happening in real life and put it in a mathematical form. At this level, we are mostly concerned with linear and first-order differential equations. A differential equation in “y” is linear if all derivatives of y appear only to the first power. So it has the form if all derivatives of y appear only to the first power. So it has the form,
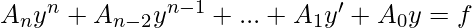
The coefficients are allowed to depend only on the independent variables. Note that the order can be arbitrarily large. We are going to look at the exact differential equations. These equations are first-order differential equations.
Exact Differential Equations
It is a first-order differential equation that looks like,
M(x, y)dx + N(x, y)dy = 0
It has a special function I(x, y) whose partial derivatives can be put in place of M and N like,
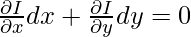
Solving these equations means finding that function I(x, y) = C.
Checking if an equation is exact or not:
Let’s assume there is a solution function I(x, y). Then,
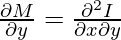
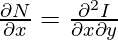
They should end up the same. So to check if the equation is exact or not, simply calculate these partial derivatives. So, now that we have checked that the equation is exact, we will move on to finding the solution to this equation.
Calculating the solution of Exact Differential Equations:
The general solution can be calculated in either of the following ways:
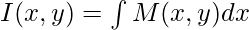 (with x as an independent variable)
(with x as an independent variable)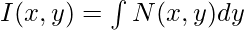 (with y as an independent variable)
(with y as an independent variable)
So, then the general solution becomes,
I(x, y) = C
Sample Problems
Question 1: Solve: (3x2y3 – 5x4)dx + (y + 3x3y2)dy = 0
Solution:
Here, M(x, y) = 3x2y3 – 5x4 and N(x, y) = y + 3x3y2
First check if this equation is exact or not,
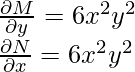
Since both of these are same, the equation is exact.
Now let’s find the solution of this equation,
I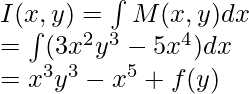
Notice that we are writing f(y) in place constant of integration “C”, because we had y as a fixed parameter while integrating it, but we know that is a variable, so we need to calculate f(y).
We know, 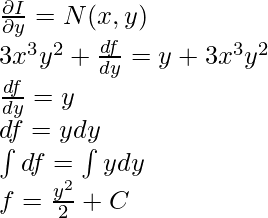
Let’s plug in f(y) in the general solution,

This is the general solution for this exact differential equation.
Question 2: Solve the differential equation for the following:
(x2+3y2)dy + 2xydx = 0
Solution:
M(x, y) = 2xy, N(x, y)=x2+3y2
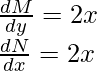
Therefore, the equation is exact.
Solution of this equation: I(x, y)=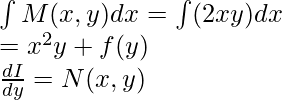
Substituting I(x, y) obtained:
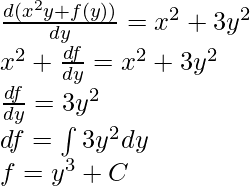
Put the value of f(y) in I(x, y):
I(x, y)= x2y+y3+C
This is the general solution for the exact differential equation.
Question 3: Solve eydx +(2y+xey)dy = 0
Solution:
M(x, y) = ey, N(x, y) = (2y+xey)
Solving 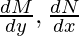
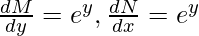
Hence, the given equation is exact equation.
Solution of the equation: I(x, y) = 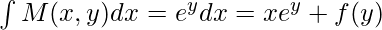
It is known that dI/dy = N(x, y)
Substituting I(x, y):
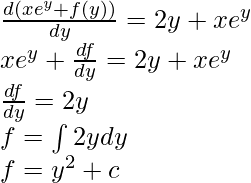
Therefore, the solution for the exact equation obtained is,
I(x, y) = xey + y2 + C
Integrating Factor
This is also yet another method for solving linear differential equations.
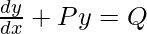
The above equation represents a linear first-order differential equation. P and Q are either constants or functions of x. The following steps give an outline of how to solve the first-order linear equation of this form using integrating factor.
Step 1: Write the given differential equation in the form 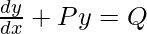 , where P and Q are either constants or functions of x only.
, where P and Q are either constants or functions of x only.
Step 2: Find the Integrating Factor 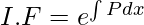
Step 3: Write the solution of the differential equation as 
Note: In case, the first-order differential equation is in the form 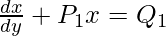 , where P1 and Q1 are constants or functions of y only. Then
, where P1 and Q1 are constants or functions of y only. Then  and the solution of the differential equation is given by
and the solution of the differential equation is given by 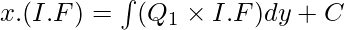
Sample Problems
Question 1: Find the general solution of the following equation,
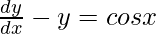
Solution:
The equation matches the form given above, so here P = -1 and Q = cosx.
Therefore, 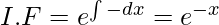
Multiplying both sides of the equation by I.F.
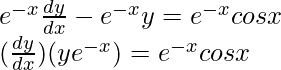
Integrating both sides of the equation by I.F, we get

Putting this value in the original equation,
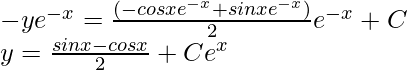
This is the general solution of the given differential equation.
Question 2: Find general solution of differential equation,
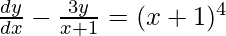
Solution:
P= -3/(x+1), Q=(x+1)4
First, find the I.F.,
I.F.=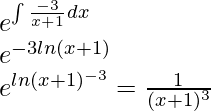
Multiply by Integrating factor on both sides:

Integrate both sides:
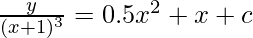
Hence, the general equation is:
y = (x+1)3(0.5x2+x+c)
Question 3: The general solution of the differential equation will be?
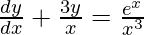
Solution:
First, find the I.F’
P = 3/x, Q = ex/x3
I.F = 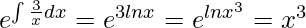
Therefore, I.F = x3
Multiply Integrating factor on both sides,
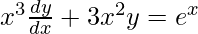
Integrate both sides,
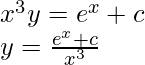
Special Integrating Factors
So far we have learned everything about Exact differential equations and how to solve them but there are times we come across certain equations which are “almost exact” but not exact differential equations since they are not Exact but are formed from exact differential equations by doing some changes in them. If we can trace back and make the equation exact again, the problem will be easily solved.
In order to trace back to the Exact integrating factor, multiply the equation with a ‘special integrating factor’ known as 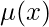 OR
OR 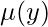 (depending upon the problem statement).
(depending upon the problem statement).
Integrating factor using only x
Suppose the almost exact equation given, M(x, y) dx + N(x, y) dy =0 [Almost Exact]
Let’s multiply this with the special integrating factor 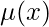
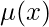 × M(x, y) dx +
× M(x, y) dx +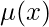 × N(x, y) dy =0
× N(x, y) dy =0
Now, in order to make the above equation exact, there has to be some value of 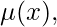 the formula for Special Integrating factor,
the formula for Special Integrating factor,
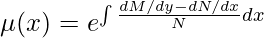
Question: Solve the differential equation, (1+y2)dx+ xydy = 0
Solution:
To begin with, we first need to check the exactness of the differential equation
dM/dy = 2y, dN/dx = y
Now, as the equation is not exact, we need to find out the integration factor that is needed to be adjusted in the equation to make it exact.
(dM/dy- dN/dx) = 2y-y = y
1/N{dM/dy- dN/dx}=y/(xy)= 1\x
Here, we figured that the equation depends on x only.
Therefore, the integrating factor is 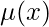
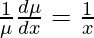
Separate the variables and integrate both sides,
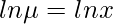
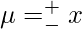
We obtained the value of integrating factor, multiply this with our original equation
(x+xy2)dx + x2ydy=0
Checking for exactness again,
dM/dy= 2xy, dN/dx= 2xy
Integrate M and N as usual,
M(x, y)= 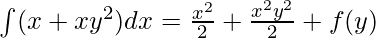
Substitute to determine f(y)
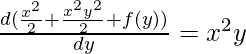
It follows f(y)=C where, C is a Constant.
Therefore, the general solution becomes,
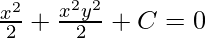
Integrating factor using only y
Similarly, the Exact equation can be obtained by multiplying the almost exact equation with the special integrating factor 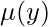 , the formula is given as,
, the formula is given as,
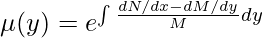
Question: Solve differential equation, (2y2+2y+4x2)dx + (2xy +x) dy = 0
Solution:
To begin with, we need to check if the following equation is exact or not,
dM/dy = (4y +2), dN/dx = (2y +1)
dM/dy ≠ dN/dx {the equation is not exact}
In order to find the Integrating factor, solve the value of 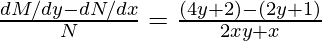
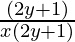 =1/x
=1/x
Since the value obtained is purely a function of x, we can conclude that the special integrating factor is 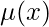
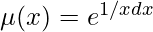 = elnx= x
= elnx= x
Multiply the special integrating factor with the original equation,
x[(2y2+2y+4x2)dx + (2xy +x) dy]=0
(2xy2+2xy+4x3)dx + (2x2y +x2) dy=0
Finding the exactness of the differential equation obtained,
dM/dy=(4xy+2x), dN/dx=(4xy+2x)
Now we can integrate M and N as usual,
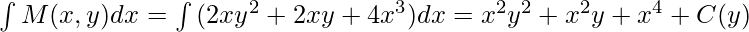
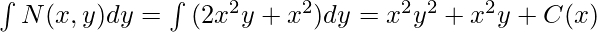
Therefore, Solution: x2y2+x2y+x4=C
Like Article
Suggest improvement
Share your thoughts in the comments
Please Login to comment...