Inverse Functions are an important concept in mathematics. To comprehend inverse functions, we can picture a function as a box that takes in inputs and produces outputs. If a function consistently generates a red-colored object as output for any input object, we can identify that box as the initial function. The box that accepts both red and normal-colored objects as inputs and generates the original colored objects as outputs, is called the inverse of the initial box.
In other words, if a function is an operation that produces an output for each input, the inverse function facilitates the identification of the specific input based on a given output. Let’s learn about inverse functions and all the different associated topics with them.

What are Inverse Functions?
If functions f(x) and g(x) are inverses of each other, then f(x) = y only if g(y) = x.
g(f(x)) = x
The figure given below describes a function and its inverse. This function is represented as f(x) and takes some input values and gives an output. The inverse of this function is denoted by f-1(x). For example, let’s say f(x) = 2x. It doubles the number which is given as input, its inverse should make them half to get back the input. f-1(x) = x/2.
Let’s say we have a function f(x) = x2. Now we are asked to find out the inverse of this function. This function is squaring its inputs, we know we need to take the square root for calculating the inverse.
f-1(x) = √x2
f-1(x) = ±x
We see that there are two answers possible, which one to choose? In such cases, the inverse is not possible. So, there are things we need to notice for the functions for which inverses are possible. Also, the function whose inverse exist is called invertible functions.
Condition for Inverse of a Function to Exist
For a function to have an inverse, the necessary and sufficient condition is
Function must be Bijective(One-One and Onto).
For example, let’s check the following graph for bijection.

This function has same values at two different values of input, this means function is not one-one. Thus, we can’t be able to find it’s inverse without restricting it’s domain.
How to Find the Inverse of a Function?
To find the inverse of a function, we need to follow the following steps:
Step 1: Substitue f(x) in the given function by “y”.
Step 2: Solve for “x” for the newly formed equation.
Step 3: Switch the positions of “x” and “y”.
Step 4: Substitute the y with notation of inverse function f -1(x).
Example: Find the inverse of f(x) = 6x + 10.
Solution:
We know, f(x) = 6x + 10. Let’s substitute y in place of f(x).
y = 6x + 10
⇒ y – 10 = 6x
⇒ x = (y – 10)/6
⇒ y = (x – 10)/6
⇒ f -1(x) = (x – 10)/6
Inverses of Common Functions
The table given below describes the inverses of some common functions which may come in handy while calculating the inverses for complex functions. The following table represents the function, its inverse, and its corner cases where corner cases describe the values which are not allowed as input to the inverse of the function.
| Function | Inverse | Corner Cases |
|---|
xn
| 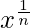
| Negative values are not allowed when n is even |
ax
| logax
| x > 0 and a > 0 |
sin(x)
| sin-1(x)
| Only values between -1 to 1 are allowed |
cos(x)
| cos-1(x)
| Only values between -1 to 1 are allowed |
tan(x)
| tan-1(x)
| —
|
Graphs of Inverse Functions
To understand the graph of the inverse function, let’s say we have f(x) = ex and assume it has inverse i.e., g(x). We know that the inverse of an exponential function is a logarithmic function. So, g(x) = logex. The figure below shows the graph for both of the functions.

We can see that both graphs are mirror images of each other with respect to the line y = x. So, we can say that the inverse of a function is a mirror image of the function when seen through the line y = x.
Note: There is no shortcut way to plot the graph of the inverse function if the graph of the original function is not given.
Inverse Functions Types
There are various types of inverse functions for common functions, some of these types are discussed as follows:
Inverse Trigonometric Function
Inverse Trigonometric Functions are the inverse functions of the trigonometric ratios, and the table for the range and domain of all the Inverse Trigonometric Functions is as follows:
Inverse Trigonometric Function
| Domain
| Range
|
|---|
sin-1(x)
| [-1, 1]
| [-π/2 , π/2]
|
cos-1(x)
| [-1, 1]
| [0, π]
|
tan-1(x)
| R
| (-π/2 , π/2)
|
sec-1(x)
| R – (-1, 1)
| [0, π] – {π/2}
|
cosec-1(x)
| R – (-1, 1)
| [ -π/2, π/2] – {0}
|
cot-1(x)
| R
| (0, π)
|
Exponential and Logarithm Function
Another example of inverse pair is the exponential and logarithm function, both are inverse of each other. For an exponential function f(x) = ax, its inverse is given by logarithm i.e., logax, and vice versa.
Learn more about, Exponential Function
Inverse Hyperbolic Function
Similar to the Inverse Trigonometric Function, there are inverse hyperbolic functions, which are the inverse of the hyperbolic trigonometric function i.e., sinh x, cosh x, tanh x, and so on. Inverse Hyperbolic Function are sinh-1, cosh-1x, tanh-1x, cosech-1x, coth-1x, and sech-1x.
People Also View:
Inverse Functions Examples
Problem 1: Find the inverse of the function f(x) = 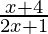
Solution:
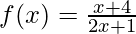
Substituting f(x) with y.
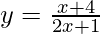
⇒ 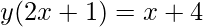
⇒ 2xy + y = x + 4
⇒ x(2y – 1) = 4 – y
⇒ x = 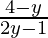
Thus, f-1(y) = 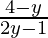
Problem 2: Find the inverse of the function f(x) = ln x + 5.
Solution:
f(x) = lnx + 5
Substituting the f(x) with y
y = lnx + 5
⇒ lnx= y – 5
⇒ x = e(y – 5)
f-1(y) = e(y – 5)
Problem 3: Find the inverse of the following function and draw its graph.
f(x) = ex + 20
Solution:
f(x) = ex + 20
Substituting the f(x) with y
⇒y = ex + 20
⇒y – 20 = ex
⇒ln(y – 20) = x
f-1(y) = ln(y – 20)
The figure below, shows the graphs for f(x) and it’s inverse.

Notice that y > 20 for this function.
Problem 4: State whether the statement is True or False. For the given function f(x) = x2 + 4, the inverse does not exist for all values of x.
Solution:
We know that f(x) = x2 + 4 is not bijective. For example,
f(-2) = 8 and f(2) = 8. So, the inverse for this function cannot exist for all values of x. Thus, this statement is called False.
Problem 5: Find the inverse for the following function:
f(x) = 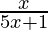
Solution:
f(x) = 
Substituting f(x) with y.

⇒ 
⇒ y(5x + 1) = x
⇒ 5xy + y = x
⇒ x(5y – 1) = -y
⇒ x =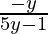
Thus, f-1(y) = 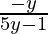
Inverse Functions Worksheet
Problem 1: f(x) = 3x + 2 Find the inverse function, f-1(x)
Problem 2: f(x) = x + 1/x − 1 Determine the inverse function, f-1(x). Note that f(x) is undefined for x = -1.
Problem 3: f(x) = √x+4 Find the inverse function, f-1(x). Assume x ≥ −4 to ensure the original function is defined.
Problem 4: f(x) = x3 + 1 Calculate the inverse function, f-1(x)
FAQs on Inverse Functions
What is an Inverse Function?
An inverse function is function which “undos” the action of a given function i.e., for a function f(x) g i called its inverse if composition of g on f gives x as output(g(f(x) = x).
When does a Function have an Inverse Function?
When a function is bijective i.e., one-one and onto at the same time, then a function can have inverse.
How do you Find the Inverse of a Function?
To find the inverse of a function, we can substitute y = f(x) in the function and then solve for x.
Result of this process i.e., the value of x, is the inverse of the given function.
What is the Notation for an Inverse Function?
The inverse of a function f(x) is denoted as f-1(x).a
What is the Relationship between a Function and its Inverse Function?
The relation between function and it’s inverse is that if we plot the graph of both functions we can see the symmetry between both the graphs about y = x line.
What is the Domain and Range of an Inverse Function?
Domain and Range of an inverse function is same as the range and domain of the original function.
Share your thoughts in the comments
Please Login to comment...