Indefinite Integrals: The derivatives have been really useful in almost every aspect of life. They allow for finding the rate of change of a function. Sometimes there are situations where the derivative of a function is available and the goal is to calculate the actual function whose derivative is given.
In these cases, integrals come into play. Intuitively they are the reverse of the differentiation process. Integrals also have a lot of applications in calculus as well as in real life. They are useful in analyzing functions and calculating the area and volumes of different arbitrary shapes.
In this article, we will discuss Indefinite Integrals, graphical interpretation, formulas, and properties.
What are Indefinite Integrals?
Integrals are also known as anti-derivatives. Integration is the inverse process of differentiation. Instead of differentiating a function, we are given the derivative of a function and are required to calculate the function from the derivative. This process is called integration or anti-differentiation. Consider a function f(x) = sin(x), the derivative of this function if f'(x) = cos(x). So, the integration of f'(x) should give back the function f(x). Notice that for every function f(x) = sin (x) + C, the derivative is the same because the constant becomes zero after differentiation. Thus, anti-derivatives are not unique, for every function, its anti-derivatives are infinite.
[Tex]\frac{d}{dx}(sin(x) + C) = cos(x)[/Tex]
This constant C is called an arbitrary constant.
A new symbol is used for denoting integrals [Tex]\int [/Tex]. This will represent the integration operation over any function. The table below represents the symbols and meanings related to integrals.
| Symbol/Term/Meaning | Meaning |
|---|
| [Tex]\int f(x)dx[/Tex] | The integral of f with respect to x |
| f(x) in [Tex]\int f(x)dx[/Tex] | Integrand |
| x in [Tex]\int f(x)dx[/Tex] | Variable of integration |
| Integral of f(x) | A function such that F'(x) = f(x) |
There are certain formulas and rules which when kept in mind, help us simplify the calculating and do it fast. The reverse power rule is one of the rules that help us in the integration of polynomials and other functions.
Reverse Power Rule
This rule helps in integrating the functions which have terms of the form xn.
[Tex]\int x^ndx = \frac{x^{n+1}}{n+1} + C[/Tex]
Here, C is the arbitrary constant, and n ≠ 1.
In this rule, the exponent of the variable is increased by 1 and then the result is divided by the new exponent value. The table below gives integrals of some standard functions.
| Function | Integral |
|---|
| sin(x) | -cos(x) |
| cos(x) | sin(x) |
| ex | ex |
| sec2(x) | tan(x) |
| [Tex]\frac{1}{x}[/Tex] | ln(x) |
Graphical Interpretation of Integrals
Apart from the usual algebraic rules of calculating the integrals. Integrals can be understood through graphs. It is clear that integrals are nothing but anti-derivatives. Consider a function f(x), and let’s say it’s anti-derivative if given by F(x). In that case, F'(x) = f(x). Consider the graph below as the graph of the function f(x), it means that the graph of the derivatives of the function F(x) is given and the goal is to determine the integral function F(x).
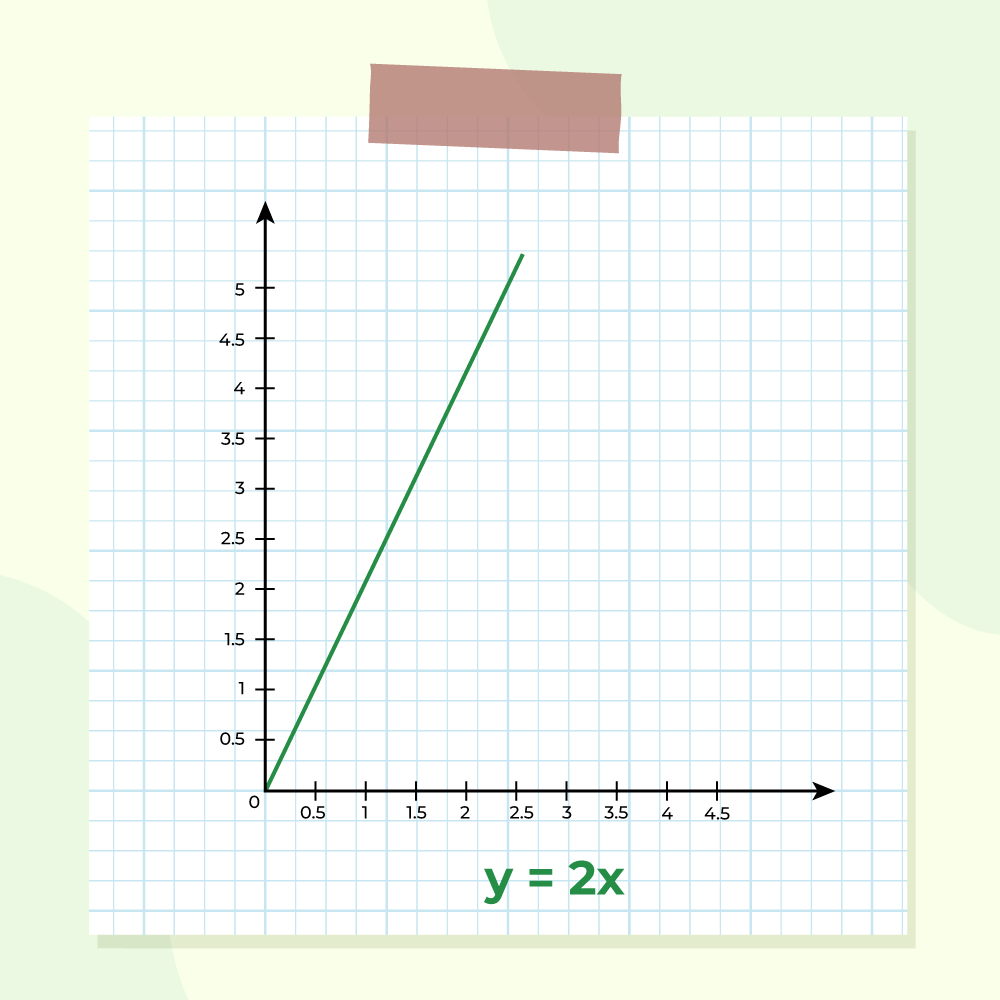
The graph shows the function f(x) = 2x, it is a straight line passing through the origin. Let’s integrate the given function using the reverse power rule mentioned above.
[Tex]\int x^ndx = \frac{x^{n+1}}{n+1} + C[/Tex]
[Tex]\int 2xdx = 2\frac{x^{2}}{2} + C[/Tex]
[Tex]\int 2xdx = x^{2} + C[/Tex]
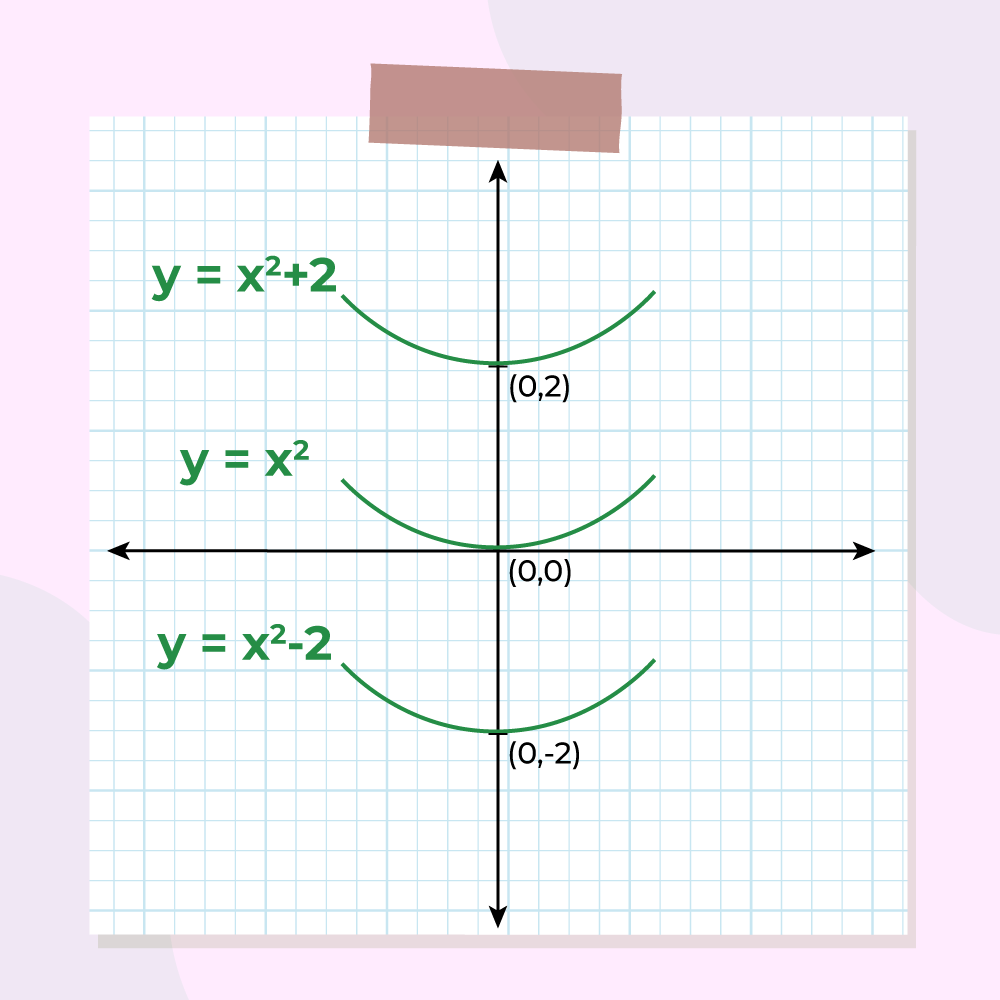
Now, when this C = 0, the equation of the integral becomes F(x) = x2, which is a parabola centred at the origin. When C =1, the parabola is shifted upwards by one unit and similarly at C = -1, the parabola is shifted downwards by one unit.
This means that function F(x) = x2 + C represents a family of curves.
Integrals by Graphs
Integrals can be determined roughly by the graphs. Integrands are nothing but the derivatives of the integrals. They give information about the rate of increase/decrease and the maxima and minima of the integrals. Let us consider a graph of a function f(x),

Assuming, F(x) = [Tex]\int f(x)dx[/Tex]
Since the derivative of the function is positive and increasing, the function will increase at an increasing rate, and the graph of the function F(x) will approximately look like a parabola that is rising upwards. The figure below gives a rough idea of the graph of the function F(x).

Calculating Indefinite Integral
Various steps to calculate the indefinite integrals are,
- Step 1: Normal indefinite integrals are solved using direct integration formulas.
- Step 2: Integrals with rational functions are solved using the partial fractions method.
- Step 3: Indefinite integrals can be solved using the substitution method.
- Step 4: Integration by parts is used to solve the integral of the function where two functions are given as a product.
Example: Find the indefinite integral ∫ x3 cos x4 dx
Solution:
Using the substitution method.
Let us assume,
x4 = t
4x3 dx = dt
Now, ∫ x3 cos x4 dx
= 1/4∫cos t dt
= 1/4 (sin t) + C
= 1/4 sin (x4 ) + C
Some of the important formulas of Indefinite Integrals are,
- ∫ 1 dx = x + C
- ∫ P dx = Px + C
- ∫ xn dx = xn + 1/ (n + 1) + C
- ∫ ex dx = ex + C
- ∫ ax dx = ax / ln a + C
- ∫1/x dx = ln |x| + C
- ∫ cos x dx = sin x + C
- ∫ sin x dx = -cos x + C
- ∫ sec2x dx = tan x + C
Properties of Indefinite Integrals
Indefinite integrals have various properties some of the various properties of Indefinite Integral are,
Property of Sum
The property of the Sum of Indefinite Integral is,
∫ [f(x) + g(x)]dx = ∫ f(x)dx + ∫ g(x)dx
Property of Difference
The property of the Difference of Indefinite Integral is,
∫ [f(x) × g(x)]dx = ∫ f(x)dx × ∫ g(x)dx
Property of Constant Multiple
The property of the Constant Multiple of Indefinite Integral is,
∫ k f(x)dx = k∫ f(x)dx
Some of the other properties of the indefinite integral are,
- ∫ f(x) dx = ∫ g(x) dx if ∫ [f(x) – g(x)]dx = 0
- ∫ [k1f1(x) + k2f2(x) + …+knfn(x)]dx = k1∫ f1(x)dx + k2∫ f2(x)dx + … + kn∫ fn(x)dx
Difference Between Indefinite Integral and Definite Integral
Indefinite integrals are used to find the integration of any function which is not bound i.e. it does not have any limit nether lower limit nor upper limit. While definite integrals give the value of the function in a limit. i.e. definite integrals are integrated over a specific interval. The indefinite integrals have a constant of integration whereas the definite integral does not have a constant of integration.
For indefinite integral,
∫ f(x) dx = F(x) + C
For definite integral,
∫abf(x) dx = F(b) – F(a)
People Also View:
Indefinite Integrals Examples
Example 1: Find the integral for the given function f(x), f(x) = sin(x) + 1
Solution:
Given f(x) = sin(x) + 1
sin(x) is a standard function, and it’s anti-derivative is,
=∫ f(x)dx
= ∫ (sin(x) + 1)dx
= [Tex]\int sin(x)dx + \int 1dx[/Tex]
= [Tex]-cos(x) + x + C[/Tex]
Example 2: Find the integral for the given function f(x), f(x) = 2ex
Solution:
Given f(x) = 2ex
ex is a standard function, and it’s anti-derivative is,
= [Tex]\int f(x)dx[/Tex]
= [Tex]\int 2e^xdx[/Tex]
Using the property 1 mentioned above,
= [Tex]2\int e^xdx[/Tex]
= 2ex + C
Example 3: Find the integral for the given function f(x), f(x) = 5x-2
Solution:
Given f(x) = 5x-2
Using the reverse power rule
= [Tex]\int f(x)dx[/Tex]
= [Tex]\int 5x^{-2}dx[/Tex]
Using the property 1 mentioned above,
= [Tex]5\int x^{-2}dx[/Tex]
= [Tex]\frac{-5}{x} + C[/Tex]
Example 4: Find the integral for the given function f(x), f(x) = sin(x) + 5cos(x)
Solution:
Given f(x) = sin(x) + 5cos(x)
sin(x) and cos(x) are standard functions, and its integral is,
= [Tex]\int f(x)dx[/Tex]
= ∫ (sin(x) + 5cos(x))dx
= [Tex]\int sin(x)dx + 5\int cos(x)dx[/Tex]
= [Tex]-cos(x) + 5sin(x) + C[/Tex]
Example 5: Find the integral for the given function f(x), f(x) = 5x-2 + x4 + x
Solution:
Given f(x) = 5x-2 + x4 + x
Using the reverse power rule
= [Tex]\int f(x)dx[/Tex]
= [Tex]\int (5x{-2} + x^4 + x)dx[/Tex]
= [Tex]\int (5x{-2} + x^4 + x)dx[/Tex]
= [Tex]5\int x^{-2}dx + \int x^4dx + \int xdx[/Tex]
= [Tex]\frac{-5}{x} + \frac{x^5}{5} + \frac{x^2}{2}[/Tex]
Example 6: Is the graph given below differentiable or not?
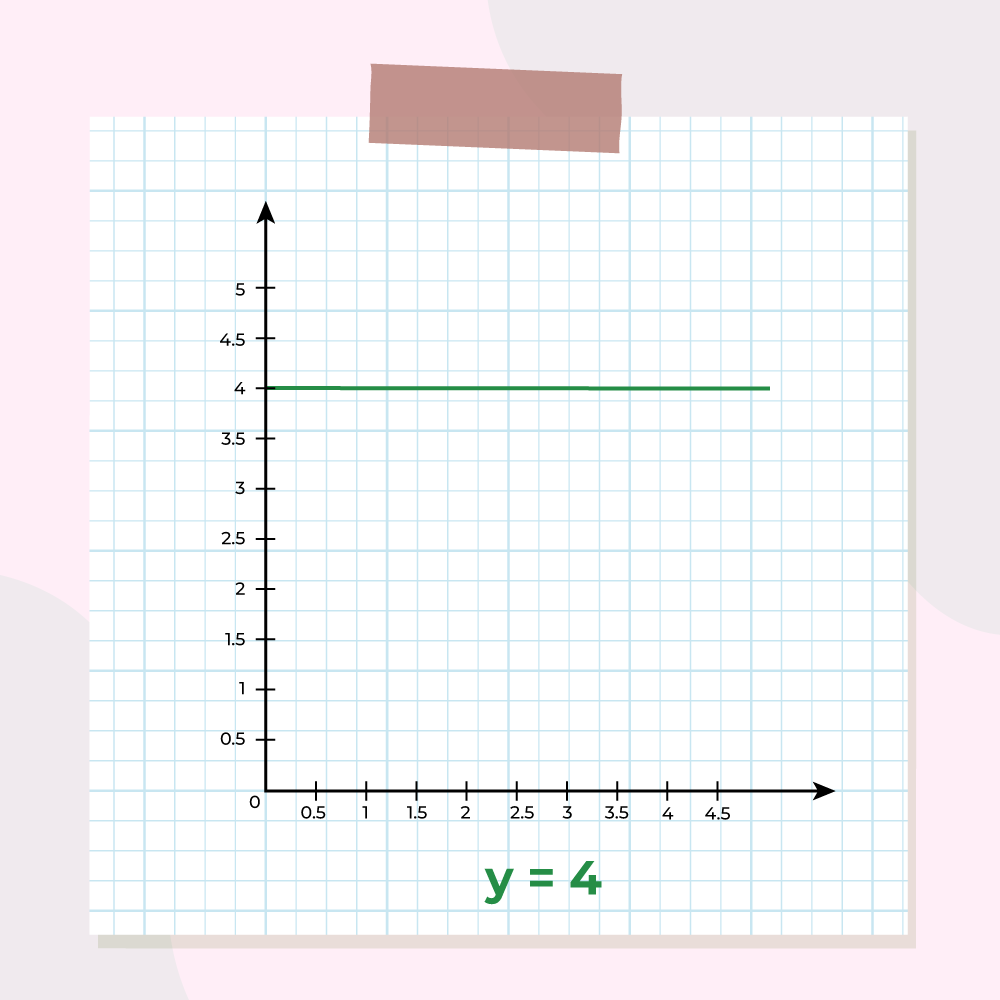
Solution:
The graph given above is, y = 4 is a constant graph.
And constant graph are easily differentiable.
Summary – Indefinite Integrals
Indefinite integrals, also known as antiderivatives, are crucial in calculus for reversing the process of differentiation. When given the derivative of a function, integration is used to find the original function, factoring in an arbitrary constant C due to the non-uniqueness of antiderivatives. Key rules and formulas, such as the reverse power rule, aid in the computation of integrals for polynomial and other standard functions. Graphical interpretations also provide insights into the behavior of integrals, illustrating how integrals can represent families of curves and depict the rate of change or the area under curves. Techniques like substitution and integration by parts are essential for solving more complex integrals, and the property of integrals, such as linearity, facilitates the integration of combined functions. Indefinite integrals differ from definite integrals in that they include an arbitrary constant and are not computed over a specified interval, emphasizing their broader conceptual use in calculus.
FAQs on Indefinite Integral
What does indefinite integral represent?
For any function F(x) whose derivative is f(x). Indefinite integrals represent the anti-derivative of the functions such that ∫f(x) dx is F(x).
Are Indefinite Integrals similar to Antiderivatives?
Yes, Indefinite Integrals are similar to antiderivative. i.e. for any function f(x) such that its derivative is f'(x) then, ∫f'(x) dx is f(x) is called its indefinite integral or anti derivative.
How do you find the indefinite integral?
Indefinite Integral of any function is calculated using the integral formulas,
∫f(x)dx = F(x) + C,
where C is constant of integration
Why do definite integrals not have C?
Definite integrals do not have a constant of integration C as the definite integral has a range in which the value of integration is calculated.
What are the boundaries of an indefinite integral?
Definite Integral is calculated in a range whereas the indefinite integral is not calculated within any boundaries.
What is the indefinite integral of any constant C?
The indefinite integral of constant C is Cx. As ∫ C dx = Cx + D, where D is the constant of integration.
What is the Indefinite Integral of ex?
Indefinite Integral of ex is ex + C it can be calculated using the formula,
∫ ex dx = ex + C
What is the difference between Indefinite Integrals and Definite Integrals?
Integrals are also called anti derivatives they can be assumed as the inverse of differentiation. The main difference between Indefinite Integrals and Definite Integrals is Indefinite integrals are evaluated without any limit whereas, definite integrals always have proper limits.
Share your thoughts in the comments
Please Login to comment...