The equation of a line in a plane is given as y = mx + C where x and y are the coordinates of the plane, m is the slope of the line and C is the intercept. However, the construction of a line is not limited to a plane only.
We know that a line is a path between two points. These two points can be located anywhere whether they could be in a single plane or they could be in space. In the case of a plane, the location of the line is characterized by two coordinates arranged in an ordered pair given as (x, y) whereas in the case of space, the location of the point is characterized by three coordinates expressed as (x, y, z).
In this article, we will learn the different forms of equations of lines in 3D space.
What is Equation of a Line?
The equation of a line is an algebraic way to express a line in terms of the coordinates of the points it joins. The equation of a line will always be a linear equation.
If we try to plot the points obtained from a linear equation it will be a straight line. The standard equation of a line is given as:
ax + by + c = 0
where,
- a and b are Coefficients of x and y
- c is Constant Term
Other forms of the equation of line are mentioned below:
Other Forms of Equation of Line
|
|---|
| Equation Name | Equation | Description |
|---|
| Point-Slope Form | (y – y1) = m(x – x1) | Represents a line using the slope (m) and a point on the line (x1, y1). |
| Slope-Intercept Form | y = mx + b | Represents a line using the slope (m) and the y-intercept (b). |
| Intercept Form | x/a + y/b = 1 | Represents a line where it intersects the x-axis at (a, 0) and the y-axis at (0, b). |
| Normal Form | x cos θ + y sin θ = p | Represents a line using the angle (θ) the line makes with the positive x-axis and the perpendicular distance (p) from the origin to the line. |
Now we will learn the equation of the line in 3D.
Equation of Line in 3D
The equation of straight line in 3D requires two points which are located in space. The location of each point is given using three coordinates expressed as (x, y, z).
The 3D Equation of a Line is given in two formats, cartesian form and vector form. In this article we will learn the Equation of a line in 3D in both Cartesian and Vector Form and also learn to derive the equation. The different cases for equation of line are listed below:
- Cartesian Form of Line
- Line Passing through two points
- Line Passing through a given point and Parallel to a given Vector
- Vector Form of line
- Line Passing through two points
- Line Passing through a given point and Parallel to a given Vector
The cartesian form of line is given by using the coordinates of two points located in space from which the line is passing. In this we will discuss two cases, when line passes through two points and when line passes through points and is parallel to a vector.
Case 1: 3D Equation of Line in Cartesian Form Passing Through Two Points
Let us assume we have two points A and B whose coordinates are given as A(x1, y1, z1) and B(x2, y2, z2).
.png)
Then the 3D equation of straight line in cartesian form is given as

where, x, y and z are rectangular coordinates.
Derivation of Equation of Line Passing through two Points
We can derive the Cartesian form of 3D Equation of Straight Line by the use of following mentioned steps:
- Step 1: Find the DR’s (Direction Ratios) by taking the difference of the corresponding position coordinates of the two given points. l = (x2 – x1), m = (y2 – y1), n = (z2 – z1); Here l, m, n are the DR’s.
- Step 2: Choose either of the two given points say, we choose (x1, y1, z1).
- Step 3: Write the required equation of the straight line passing through the points (x1, y1, z1) and (x2, y2, z2).
- Step 4: The 3D equation of straight line in cartesian form is given as L : (x – x1)/l = (y – y1)/m = (z – z1)/n = (x – x1)/(x2 – x1) = (y – y1)/(y2 – y1) = (z – z1)/(z2 – z1)
Where (x, y, z) are the position coordinates of any variable point lying on the straight line.
Example: If a straight line is passing through the two fixed points in the 3-dimensional whose position coordinates are P (2, 3, 5) and Q (4, 6, 12) then its cartesian equation using the two-point form is given by
Solution:
l = (4 – 2), m = (6 – 3), n = (12 – 5)
l = 2, m = 3, n = 7
Choosing the point P (2, 3, 5)
The required equation of the line
L: (x – 2) / 2 = (y – 3) / 3 = (z – 5) / 7
Case 2: 3D Equation of Line in Cartesian Passing through a Point and Parallel to a given Vector
Let us assume the line passes through a point P(x1, y1, z1) and is parallel to a vector given as  .
.
.png)
Then the equation of line is given as

where, x, y, z are rectangular coordinates and a, b, c are direction cosines.
Derivation of 3D Equation of Line in Cartesian Passing through a Point and Parallel to a given Vector
Let us assume we have a point P whose position vector is given as  from the origin. Let the line that passes through P is parallel to another vector
from the origin. Let the line that passes through P is parallel to another vector  . Let us take a point R on the line that passes through P, then the position vector of R is given as
. Let us take a point R on the line that passes through P, then the position vector of R is given as  .
.
Since, PR is parallel to  ⇒
⇒ 
Now if we move on the line PR then the coordinate of any point that lies on the line will have the coordinate in the form of (x1 + λa), (y1 + λb), (z1 + λc), where λ is a parameter whose value ranges from -∞ to +∞ depending on the direction from P where we move.
Hence, the coordinates of the new point will be
x = x1 + λa ⇒ λ = x – x1/a
y = y1 + λb ⇒ λ = y – y1/b
z = z1 + λc ⇒ λ = z – z1/c
Comparing the above three equations we have the equation of line as

Example: Find the Equation of a Line passing through a point (2, 1, 3) and parallel to a vector 3i – 2j + k
Solution:
The Equation of line passing through a point and parallel to a vector is given as
(x – x1)/a = (y – y1)/b = (z – z1)/c
From the question we have, x1 = 2, y1 = 1, z1 = 3 and a = 3, b = -2 and c = k. Hence, the required equation of the line will be
⇒ (x – 2)/3 = (y – 1 )/-2 = (z – 3)/1
Vector Form of the Equation of Line in 3D is given using a vector equation that involves the position vector of the points. In this heading, we will obtain the 3D Equation of the line in vector form for two cases.
Case 1: 3D Equation of Line Passing through Two Points in Vector Form
Let us assume we have two points A and B whose position vector is given as 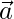 and
and 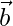 .
.
.png)
Then the vector equation of the Line L is given as

where  is the distance between two points and λ is the parameter that lies on the line.
is the distance between two points and λ is the parameter that lies on the line.
Derivation of 3D Equation of Line Passing through Two Points in Vector Form
Suppose we have two points A and B whose position vector is given as 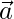 and
and 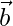 . Now we know that a line is the distance between any two points. Hence, we need to subtract the two position vectors to obtain the distance.
. Now we know that a line is the distance between any two points. Hence, we need to subtract the two position vectors to obtain the distance.
⇒ 
Now we know that any point on this line will be given as the sum of position vector  with the product of the parameter λ and the position vector of the distance between two points i.e.
with the product of the parameter λ and the position vector of the distance between two points i.e. 
Hence, the equation of the line in the vector form will be  or
or 
Example: Find the vector equation of a line in 3D that passes through two points whose position vectors are given as 2i + j – k and 3i + 4j + k
Solution:
Given that the two position vectors are given as 2i + j – k and 3i + 4j + k
Distance d = (3i + 4j + k) – (2i + j -k) = i + 3j + 2k
We know that equation of the line is given as 
Hence, the equation of the line will be  = 2i + j – k + λ(i + 3j + 2k)
= 2i + j – k + λ(i + 3j + 2k)
Case 2: Vector Form of 3D Equation of Line Passing through a Point and Parallel to a Vector
Let’s say we have a point P whose position vector is given as  . Let this line be parallel to another line whose position vector is given as
. Let this line be parallel to another line whose position vector is given as  .
.
.png)
Then the vector equation of the line ‘l’ is given as

where λ is the parameter that lies on the line.
Derivation of the Vector Form of 3D Equation of Line Passing through a Point and Parallel to a Vector
Consider a point P whose position vector is given as  . Now let us assume this line is parallel to a vector
. Now let us assume this line is parallel to a vector  then, the equation of the line will be
then, the equation of the line will be  . Now since the line also passes through point P, then as we move away from Point P in either direction on the line then the position vector of the point will be in the form of
. Now since the line also passes through point P, then as we move away from Point P in either direction on the line then the position vector of the point will be in the form of  . Hence, the equation of the line will be
. Hence, the equation of the line will be  where λ is the parameter that lies on the line.
where λ is the parameter that lies on the line.
Example: Find the Vector Form of the Equation of the line passing through the point (-1, 3, 2) and parallel to a vector 5i + 7j – 3k.
Solution:
We know that the vector form of the equation of a line passing through a point and parallel to a vector is given as 
Given that the point is (-1, 3, 2), hence the position vector of the point will be -i + 3j + 2k and the given vector is 5i + 7j – 3k.
Therefore, the required equation of the line will be  = (-i + 3j + 2k) + λ(5i + 7j – 3k).
= (-i + 3j + 2k) + λ(5i + 7j – 3k).
| Name | Formula | Description |
|---|
| Vector Form | r = a + λ d | Represents a line through point (a) parallel to direction vector (d). λ is the parameter. |
|---|
| Parametric Form | x = x₀ + λ a, y = y₀ + λ b, z = z₀ + λ c | Describes a line using parameter (λ or t) for varying positions. (x₀, y₀, z₀) is a point on the line, (a, b, c) is the direction vector. |
|---|
| Shortest Distance Between Skew Lines | (Formula varies depending on specific approach) | Calculates the perpendicular distance between two non-intersecting lines. |
|---|
| Equation of a Line Through Two Points | x = x₀ + t a, y = y₀ + t b, z = z₀ + t c | Represents a line connecting points ((x₀, y₀, z₀)) and ((x, y, z)). t is the parameter, (a, b, c) is the direction vector. |
|---|
Similar Reads
Solved Examples on Equation of a Line in 3D
Practice equations of line in 3D with these solved practice questions.
Example 1: If a straight line is passing through the two fixed points in the 3-dimensional whose position vectors are (2 i + 3 j + 5 k) and (4 i + 6 j + 12 k) then its Vector equation using the two-point form is given by
Solution:
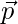 = (4 i + 6 j + 12 k) – (2 i + 3 j + 5 k)
= (4 i + 6 j + 12 k) – (2 i + 3 j + 5 k)
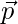 = (2 i + 3 j + 7 k) ; Here
= (2 i + 3 j + 7 k) ; Here 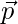 is a vector parallel to the straight line
is a vector parallel to the straight line
Choosing the position vector (2 i + 3 j + 5 k)
The required equation of the straight line
L : 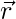 = (2 i + 3 j + 5 k) + t . (2 i + 3 j + 7 k)
= (2 i + 3 j + 5 k) + t . (2 i + 3 j + 7 k)
Example 2: If a straight line is passing through the two fixed points in the 3-dimensional space whose position coordinates are (3, 4, -7) and (1, -1, 6) then its vector equation using the two-point form is given by
Solution:
Position vectors of the given points will be (3 i + 4 j – 7 k) and (i – j + 6 k)
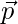 = (3 i + 4 j – 7 k) – (i – j + 6 k)
= (3 i + 4 j – 7 k) – (i – j + 6 k)
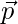 = (2 i + 5 j – 13 k) ; Here
= (2 i + 5 j – 13 k) ; Here 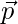 is a vector parallel to the straight line
is a vector parallel to the straight line
Choosing the position vector (i – j + 6 k)
The required equation of the straight line
L : 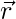 = (i – j + 6 k) + t . (2 i + 5 j – 13 k)
= (i – j + 6 k) + t . (2 i + 5 j – 13 k)
Example 3: If a straight line is passing through the two fixed points in the 3-dimensional whose position vectors are (5 i + 3 j + 7 k) and (2 i + j – 3 k) then its Vector equation using the two-point form is given by
Solution:
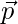 = (5 i + 3 j + 7 k) – (2 i + j – 3 k)
= (5 i + 3 j + 7 k) – (2 i + j – 3 k)
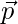 = (3 i + 2 j + 10 k) ; Here
= (3 i + 2 j + 10 k) ; Here 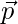 is a vector parallel to the straight line
is a vector parallel to the straight line
Choosing the position vector (2 i + j – 3 k)
The required equation of the straight line
L: 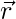 = (2 i + j – 3 k) + t . (3 i + 2 j + 10k)
= (2 i + j – 3 k) + t . (3 i + 2 j + 10k)
Example 4: If a straight line is passing through the two fixed points in the 3-dimensional whose position coordinates are A (2, -1, 3) and B (4, 2, 1) then its cartesian equation using the two-point form is given by
Solution:
l = (4 – 2), m = (2 – (-1)), n = (1 – 3)
l = 2, m = 3, n = -2
Choosing the point A (2, -1, 3)
The required equation of the line
L : (x – 2) / 2 = (y + 1) / 3 = (z – 3) / -2 or
L : (x – 2) / 2 = (y + 1) / 3 = (3 – z) / 2
Example 5: If a straight line is passing through the two fixed points in the 3-dimensional whose position coordinates are X (2, 3, 4) and Y (5, 3, 10) then its cartesian equation using the two-point form is given by
Solution:
l = (5 – 2), m = (3 – 3), n = (10 – 4)
l = 3, m = 0, n = 6
Choosing the point X (2, 3, 4)
The required equation of the line
L : (x – 2) / 3 = (y – 3) / 0 = (z – 4) / 6 or
L : (x – 2) / 1 = (y – 3) / 0 = (z – 4) / 2
Equation of a Line in 3D – FAQs
What is Equation of a Line in 3D?
The Equation of a Line in 3D is given as (x – x1)/(x2 – x1) = (y – y1)/(y2 – y1) = (z – z1)/(z2 – z1)
What is Cartesian Form of the Equation of a Line in 3D?
Cartesian Form of the Equation of Line in 3D is given for two cases
Case 1: When the line passes through two points: 
Case 2: When a line passes through one point and is parallel to a vector: 
What is Vector Form of Equation of a Line in 3D?
Vector form of the equation of a line in 3D is given for two cases:
Case 1: Line Passing through two Points: 
Case 2: Line Pass Through a Point and Parallel to a vector: 
What is Slope Point Equation of a Line?
Slope Point Equation of a line is given as y = mx + C where m is the slope
What is the Standard Equation of a Line?
Standard equation of a line is ax + by + c = 0
Like Article
Suggest improvement
Share your thoughts in the comments
Please Login to comment...