Angles Between two Lines in 3D Space: Solved Examples
Last Updated :
18 Apr, 2024
Straight Lines in 3D space are generally represented in two forms Cartesian Form and Vector Form. Hence the angles between any two straight lines in 3D space are also defined in terms of both the forms of the straight lines. Let’s discuss the methods of finding the angle between two straight lines in both forms one by one.
Cartesian Form
L1: (x – x1) / a1 = (y – y1) / b1 = (z – z1) / c1
L2: (x – x2) / a2 = (y – y2) / b2 = (z – z2) / c2
Here L1 & L2 represent the two straight lines passing through the points (x1, y1, z1) and (x2, y2, z2) respectively in 3D space in Cartesian Form.
- Direction ratios of line L1 are a1, b1, c1 then a vector parallel to L1 is
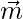 1 = a1 i + b1 j + c1 k
1 = a1 i + b1 j + c1 k - Direction ratios of line L2 are a2, b2, c2 then a vector parallel to L2 is
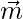 2 = a2 i + b2 j + c2 k
2 = a2 i + b2 j + c2 k
Then the angle ∅ between L1 and L2 is given by:
∅ = cos-1{(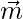 1 .
1 . 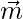 2) / (|
2) / (|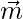 1| × |
1| × |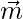 2|)}
2|)}
Examples
Example 1: (x – 1) / 1 = (2y + 3) / 3 = (z + 5) / 2 and (x – 2) / 3 = (y + 1) / -2 = (z – 2) / 0 are the two lines in 3D space then the angle ∅ between them is given by:
Solution:
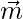 1 = 1 i + (3 / 2) j + 2 k
1 = 1 i + (3 / 2) j + 2 k
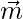 2 = 3 i – 2 j + 0 k
2 = 3 i – 2 j + 0 k
|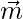 1| = √(12 + (3/2)2 + 22) = √(29 / 2)
1| = √(12 + (3/2)2 + 22) = √(29 / 2)
|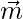 2| = √(32 + 22 + 02) = √(13)
2| = √(32 + 22 + 02) = √(13)
∅ = cos-1{(1×3 + (3/2)×(-2) + (2)×0 ) / ((√(29) / 2) × √(13))}
∅ = cos-1{0 / ((√(29) / 2) × √(13))}
∅ = cos-1(0)
∅ = π / 2
Example 2: Find the angles between the two lines in 3D space whose only direction ratios are given 2, 1, 2 and 2, 3, 1. In the question, equations of the 2 lines are not given, only their DRs are given. So the angle ∅ between the 2 lines is given by:
Solution:
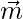 1 = Vector parallel to the line having DRs 2, 1, 2 = (2 i + j + 2 k)
1 = Vector parallel to the line having DRs 2, 1, 2 = (2 i + j + 2 k)
|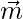 1| = √(22 + 12 + 22) = √9 = 3
1| = √(22 + 12 + 22) = √9 = 3
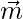 2 = Vector parallel to the line having DRs 2, 3, 1 = (2 i + 3 j + k)
2 = Vector parallel to the line having DRs 2, 3, 1 = (2 i + 3 j + k)
|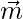 2| = √(22 + 32 + 12) = √(14)
2| = √(22 + 32 + 12) = √(14)
∅ = cos-1{(2×2 + 1×3 + 2×1) / (3 × √(14))}
∅ = cos-1{(4 + 3 + 2) / (3 × √(14))}
∅ = cos-1{9 / (3 × √(14))}
∅ = cos-1(3 / √(14))
Example 3: (x – 1) / 2 = (y – 2) / 1 = (z – 3) / 2 and (x – 2) / 2 = (y – 1) / 2 = (z – 3) / 1 are the two lines in 3D space then the angle ∅ between them is given by:
Solution:
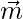 1 = 2 i + j + 2 k
1 = 2 i + j + 2 k
|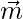 1| = √(22 + 12 + 22) = √9 = 3
1| = √(22 + 12 + 22) = √9 = 3
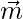 2 = 2 i + 2 j + k
2 = 2 i + 2 j + k
|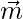 2| = √(22 + 22 + 12) = √9 = 3
2| = √(22 + 22 + 12) = √9 = 3
∅ = cos-1{(2×2 + 1×2 + 2×1 ) / (3 × 3)}
∅ = cos-1{(4 + 2 + 2) / 9}
∅ = cos-1(8 / 9)
Vector Form
L1: 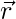 =
= 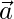 1 + t .
1 + t .  1
1
L2: 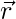 =
= 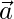 2 + u .
2 + u .  2
2
Here L1 & L2 represent the two straight lines passing through the points whose position vectors are 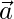 1 and
1 and 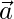 2 respectively in 3D space in Vector Form.
2 respectively in 3D space in Vector Form.  1 &
1 &  2 are the two vectors parallel to L1 and L2 respectively and t & u are the parameters. Then the angle ∅ between the vectors
2 are the two vectors parallel to L1 and L2 respectively and t & u are the parameters. Then the angle ∅ between the vectors  1 and
1 and  2 is equals to the angle between L1 and L2 is given by:
2 is equals to the angle between L1 and L2 is given by:
∅ = cos-1{( 1 .
1 .  2) / (|
2) / (| 1| × |
1| × | 2|)}
2|)}
Examples
Example 1: 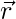 = (i + j + k) + t × {(-√3 – 1) i + (√3 – 1) j + 4 k} and
= (i + j + k) + t × {(-√3 – 1) i + (√3 – 1) j + 4 k} and 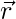 = (i + j + k) + u × (i + j + 2 k) are the two lines in 3D space then the angle ∅ between them is given by:
= (i + j + k) + u × (i + j + 2 k) are the two lines in 3D space then the angle ∅ between them is given by:
Solution:
 1 = (-√3 – 1) i + (√3 – 1) j + 4 k
1 = (-√3 – 1) i + (√3 – 1) j + 4 k
| 1| = √{(-√3 – 1)2 + (√3 – 1)2 + 42)} = √(24)
1| = √{(-√3 – 1)2 + (√3 – 1)2 + 42)} = √(24)
 2 = i + j + 2 k
2 = i + j + 2 k
| 2| = √(12 + 12 + 22) = √6
2| = √(12 + 12 + 22) = √6
∅ = cos-1{(-√3 – 1)×1 + (√3 – 1)×1 + 4×2 ) / (√(24) × √6)}
∅ = cos-1{6 / (√(24) × √6)}
∅ = cos-1(½)
∅ = π / 3
Example 2: (i + 2 j + 2 k) and (3 i + 2 j + 6 k) are the two vectors parallel to the two lines in 3D space then the angle ∅ between them is given by:
Solution:
 1 = i + 2 j + 2 k
1 = i + 2 j + 2 k
| 1| = √(12 + 22 + 22)} = √9 = 3
1| = √(12 + 22 + 22)} = √9 = 3
 2 = 3 i + 2 j + 6 k
2 = 3 i + 2 j + 6 k
| 2| = √(32 + 22 + 62) = √(49) = 7
2| = √(32 + 22 + 62) = √(49) = 7
∅ = cos-1{(1×3 + 2×2 + 2×6) / (7 × 3)}
∅ = cos-1{(3 + 4 + 12) / 21}
∅ = cos-1(19 / 21)
Example 3: 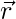 = (3 i + 5 j + 7 k) + s × {(i + 2 j – 2 k} and
= (3 i + 5 j + 7 k) + s × {(i + 2 j – 2 k} and 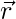 = (4 i + 3 j + k) + t × (2 i + 4 j – 4 k) are the two lines in 3D space then the angle ∅ between them is given by:
= (4 i + 3 j + k) + t × (2 i + 4 j – 4 k) are the two lines in 3D space then the angle ∅ between them is given by:
Solution:
 1 = i + 2 j – 2 k
1 = i + 2 j – 2 k
| 1| = √(12 + 22 + (-2)2)} = √9 = 3
1| = √(12 + 22 + (-2)2)} = √9 = 3
 2 = 2 i + 4 j – 4 k
2 = 2 i + 4 j – 4 k
| 2| = √(22 + 42 + (-4)2) = √(36) = 6
2| = √(22 + 42 + (-4)2) = √(36) = 6
∅ = cos-1{(1×2 + 2×4 + (-2)×(-4)) / (3 × 6)}
∅ = cos-1{(2 + 8 + 8) / 18}
∅ = cos-1(18 / 18)
∅ = cos-1(1) = 0
Share your thoughts in the comments
Please Login to comment...