Properties of Definite Integrals
Last Updated :
27 Feb, 2024
An integral that has a limit is known as a definite integral. It has an upper limit and a lower limit. It is represented as
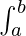 f(x) = F(b) − F(a)
f(x) = F(b) − F(a)
There are many properties regarding definite integral. We will discuss each property one by one with proof.
Properties of Definite Integrals
Various properties of the definite integrals are added below,
Property 1: 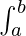 f(x) dx =
f(x) dx = 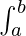 f(y) dy
f(y) dy
Proof:
 f(x) dx…….(1)
f(x) dx…….(1)
Suppose x = y
dx = dy
Putting this in equation (1)
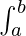 f(y) dy
f(y) dy
Property 2:  f(x) dx = –
f(x) dx = –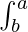 f(x) dx
f(x) dx
Proof:
 f(x) dx = F(b) – F(a)……..(1)
f(x) dx = F(b) – F(a)……..(1)
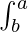 f(x) dx = F(a) – F(b)………. (2)
f(x) dx = F(a) – F(b)………. (2)
From (1) and (2)
We can derive  f(x) dx = –
f(x) dx = –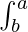 f(x) dx
f(x) dx
Property 3:  f(x) dx =
f(x) dx = 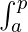 f(x) dx +
f(x) dx + 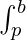 f(x) dx
f(x) dx
Proof:
 f(x) dx = F(b) – F(a) ………..(1)
f(x) dx = F(b) – F(a) ………..(1)
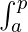 f(x) dx = F(p) – F(a) ………..(2)
f(x) dx = F(p) – F(a) ………..(2)
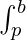 f(x) dx = F(b) – F(p) ………..(3)
f(x) dx = F(b) – F(p) ………..(3)
From (2) and (3)
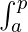 f(x) dx +
f(x) dx +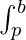 f(x) dx = F(p) – F(a) + F(b) – F(p)
f(x) dx = F(p) – F(a) + F(b) – F(p)
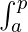 f(x) dx +
f(x) dx + 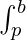 f(x) dx = F(b) – F(a) =
f(x) dx = F(b) – F(a) =  f(x) dx
f(x) dx
Hence, it is Proved.
Property 4.1:  f(x) dx =
f(x) dx =  f(a + b – x) dx
f(a + b – x) dx
Proof:
Suppose
a + b – x = y…………(1)
-dx = dy
From (1) you can see
when x = a
y = a + b – a
y = b
and when x = b
y = a + b – b
y = a
Replacing by these values he integration on right side becomes 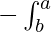 f(y)dy
f(y)dy
From property 1 and property 2 you can say that
 f(x) dx =
f(x) dx =  f(a + b – x) dx
f(a + b – x) dx
Property 4.2: If the value of a is given as 0 then property 4.1 can be written as
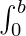 f(x) dx =
f(x) dx = 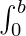 f(b – x) dx
f(b – x) dx
Property 5:  f(x) dx =
f(x) dx =  f(x) dx +
f(x) dx +  f(2a – x) dx
f(2a – x) dx
Proof:
We can write  f(x) dx as
f(x) dx as
 f(x) dx =
f(x) dx =  f(x) dx +
f(x) dx + 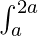 f(x) dx ………….. (1)
f(x) dx ………….. (1)
I = I1 + I2
(from property 3)
Suppose 2a – x = y
-dx = dy
Also when x = 0
y = 2a, and when x = a
y = 2a – a = a
So,  f(2a – x)dx can be written as
f(2a – x)dx can be written as
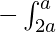 f(y) dy = I2
f(y) dy = I2
Replacing equation (1) with the value of I2 we get
 f(x) dx =
f(x) dx =  f(x) dx +
f(x) dx +  f(2a – x) dx
f(2a – x) dx
Property 6 : 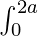 f(x) dx = 2
f(x) dx = 2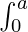 f(x) dx; if f(2a – x) = f(x)
f(x) dx; if f(2a – x) = f(x)
= 0; if f(2a – x) = -f(x)
Proof:
From property 5 we can write  f(x) dx as
f(x) dx as
 f(x) dx =
f(x) dx = f(x) dx +
f(x) dx +  f(2a – x) dx ………….(1)
f(2a – x) dx ………….(1)
Part 1: If f(2a – x) = f(x)
Then equation (1) can be written as
 f(x) dx =
f(x) dx = f(x) dx +
f(x) dx +  f(x) dx
f(x) dx
This can be further written as
 f(x) dx = 2
f(x) dx = 2  f(x) dx
f(x) dx
Part 2: If f(2a – x) = -f(x)
Then equation (1) can be written as
 f(x) dx=
f(x) dx=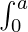 f(x) dx –
f(x) dx –  f(x) dx
f(x) dx
This can be further written as
 f(x) dx= 0
f(x) dx= 0
Property 7: 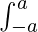 f(x) dx = 2
f(x) dx = 2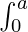 f(x) dx; if a function is even i.e. f(-x) = f(x)
f(x) dx; if a function is even i.e. f(-x) = f(x)
= 0; if a function is odd i.e. f(-x) = -f(x)
Proof:
From property 3 we can write
 f(x) dx as
f(x) dx as
 f(x) dx =
f(x) dx = 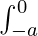 f(x) dx +
f(x) dx +  f(x) dx ………(1)
f(x) dx ………(1)
Suppose
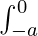 f(x) dx = I1 ……(2)
f(x) dx = I1 ……(2)
Now, assume x = -y
So, dx = -dy
And also when x = -a then
y= -(-a) = a
and when x = 0 then, y = 0
Putting these values in equation (2) we get
I1 = 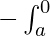 f(-y)dy
f(-y)dy
Using property 2, I1 can be written as
I1 =  f(-y)dy
f(-y)dy
and using property 1 I1 can be written as
I1 =  f(-x)dx
f(-x)dx
Putting value of I1 in equation (1), we get
 f(x) dx =
f(x) dx =  f(-x) dx +
f(-x) dx + f(x) dx ……….(3)
f(x) dx ……….(3)
Part 1: When f(-x) = f(x)
Then equation(3) becomes
 f(x) dx =
f(x) dx =  f(x) dx +
f(x) dx +  f(x) dx
f(x) dx
 f(x) dx = 2
f(x) dx = 2 f(x) dx
f(x) dx
Part 2: When f(-x) = -f(x)
Then equation 3 becomes
 f(x) dx = –
f(x) dx = – f(x) dx +
f(x) dx + f(x) d
f(x) d
 f(x)dx = 0
f(x)dx = 0
Example on Properties of Definite Integrals
Example 1: I = 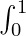 x(1 – x)99 dx
x(1 – x)99 dx
Solution:
Using property 4.2 he given question can be written as
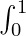 (1 – x) [1 – (1 – x)]99 dx
(1 – x) [1 – (1 – x)]99 dx
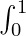 (1 – x) [1 – 1 + x]99 dx
(1 – x) [1 – 1 + x]99 dx
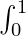 (1 – x)x99 dx
(1 – x)x99 dx
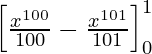
= 1/100 – 1/101
= 1 / 10100
Example 2: I =  cos(x) log
cos(x) log 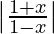
Solution:
f(x) = cos(x) log 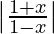
f(-x) = cos(-x) log 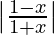
f(-x) = -cos(x) log 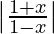
f(-x) = -f(x)
Hence the function is odd. So, Using property
 f(x)dx = 0; if a function is odd i.e. f(-x) = -f(x)
f(x)dx = 0; if a function is odd i.e. f(-x) = -f(x)
 cos(x) log
cos(x) log  = 0
= 0
Example 3: I =  [x] dx
[x] dx
Solution:
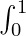 0 dx +
0 dx +  1 dx +
1 dx + 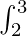 2 dx +
2 dx +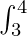 3 dx +
3 dx + 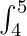 4 dx [using Property 3]
4 dx [using Property 3]
= 0 + [x]21 + 2[x]32 + 3[x]43 + 4[x]54
= 0 + (2 – 1) + 2(3 – 2) + 3(4 – 3) + 4(5 – 4)
= 0 + 1 + 2 + 3 + 4
= 10
Example 4: I = 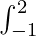 |x| dx
|x| dx
Solution:
 (-x) dx +
(-x) dx + 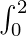 (x) dx [using Property 3]
(x) dx [using Property 3]
= -[x2/2]0-1 + [x2/2]20
= -[0/2 – 1/2] + [4/2 – 0]
= 1/2 + 2
= 5/2
Like Article
Suggest improvement
Share your thoughts in the comments
Please Login to comment...