Mean Value Theorem is one of the important theorems in calculus. These theorems are used in Mathematics to solve various problems. Mean Value Theorem is abbreviated as MVT. This theorem was first proposed by an Indian Mathematician Parmeshwara early 14th century. After this various mathematicians from all around the world works on this theorem and the final theorem was proposed by Augustin Louis Cauchy in the year 1823.
According to Mean Value Theorem for a curve passing through two given points there exist at least one point on the curve where the tangent is parallel to the secant passing through the two given points.
Let’s learn about Mean Value Theorem its Geometrical Interpretation and others in detail in this article.
What is Mean Value Theorem?
Mean Value Theorem states that for any function f(x) passing through two given points [a, f(a)], [b, f(b)], there exist at least one point [c, f(c)] on the curve such that the tangent through that point is parallel to the secant passing through the other two points.
In calculus, for a function f(x) defined on [a, b] → R, such that it is continuous and differentiable across an interval. Then mean value theorem is applicable when
- Function f(x) is continuous over the interval [a, b].
- Function f(x) is differentiable over the interval (a, b).
Then, there exists a point c in the interval (a, b) such that
f'(c) = [ f(b) – f(a) ] / (b – a)
Mean Value Theorem Proof
Statement: If a function f(x) is continuous over the closed interval [a, b], and differentiable over the open interval (a, b), then there exists at least one point c in the interval (a, b) such that f ‘(c) is zero, i.e. the tangent to the curve at point [c, f(c)] is parallel to the x-axis.
Proof:
We know that the secant line to f(x) passes through [a, f(a)] and [b, f(b)].
Now, the equation of the line passing through two given points (x1, y1) and (x2, y2) is y – y1 = [(y2 – y1)/(x2 – x1)](x – x1)
The equation of the secant line is,
F(x) – f(a) = [f(b) – f(a)] / (b – a) (x-a)
F(x) = [ f(b) – f(a) ] / (b – a) (x-a) + f(a) …(i)
Let, h(x) be F(x) – g(x)
h(x) = F(x) – [[ f(b) – f(a) ] / (b – a) (x-a) + f(a)] (From (i))
As, h(x) is continuous on [a, b] and differentiable on (a, b) and h(a) = h(b) = 0
Applying, Rolles theorem, we get an
x = c in (a, b) such that h'(c) = 0
Now,
h'(x) = f'(x) – [ f(b) – f(a) ] / (b – a)
h'(c) = f'(c) – [ f(b) – f(a) ] / (b – a) = 0
f'(c) = [ f(b) – f(a) ] / (b – a)
Thus the Mean Value Theorem is verified.
This result is true only for the function f(x) which is continuous and differentiable on the interval (a, b)
Mean Value Theorem Graphical Representation
Mean Value Theorem can be easily interpreted using its graphical representation. Graphically mean value theorem state that for any function f(x) which is continuous on the closed interval [a, b] and differentiable on the open interval (a, b) there exists a point ‘c’ in the closed [a, b] such that at [f(c), c] point on the curve, the tangent at that point is parallel to the secant drawn between the initial two points [a, f(a)] and [b, f(b)].
We know that,
Slope at any point c on the curve f(x) = f'(c)
Slope of the line passing through [a, f(a)] and [b, f(b)] = [ f(b) – f(a) ] / (b – a)
Now according to the mean value theorem graphical representation
Slope of the Tangent = Slope of the Secant
f'(c) = [ f(b) – f(a) ] / (b – a)
Difference Between Mean Value Theorem and Rolle’s Theorem
Both the mean value theorem and Rolle’s theorem define the function f(x) such that it is continuous across the interval [a, b], and it is differentiable across the interval (a, b). In the mean value theorem, the two referred points (a, f(a)), (b, f(b)) are distinct and f(a) ≠ f(b). In Rolle’s theorem, the points are defined such that f(a) = f(b).
The value of c in the mean value theorem is defined such that the slope of the tangent at the point (c, f(c)) is equal to the slope of the secant joining the two points. The value of c in Rolle’s theorem is defined such that the slope of the tangent at the point (c, f(c)) is equal to the slope of the x-axis. The slope in the mean value theorem is f'(c) = [ f(b) – f(a) ] / (b – a), and the slope in Rolle’s theorem is equal to f'(c) = 0.
Learn more about, Rolle’s Theorem and Lagrange’s Mean Value Theorem
Cauchy Mean Value Theorem
Cauchy Mean Value Theorem is another important mean value theorem which is the extension of the mean value theorem.
Statement:
Let, f(x) and g(x) are the functions defined on [a, b] such that, f(x) and g(x) both are continuous on [a, b] and f(x) and g(x) both are differentiable on (a, b), then there exists at least one point c ∈ (a, b) such that
f'(c) / g'(c) = { f(b) – f(a)} / {g(b) – g(a)}
OR
f'(c) {g(b) – g(a)}= g'(c){ f(b) – f(a)}
This the Cauchy Mean Value Theorem.
If we take, g(x) = x for every x ∈ [a,b] in the above theorem, we get
f'(c) = { f(b) – f(a)} / {b-a}
This is the statement of Langrange’s mean value theorem.
Generalized Mean Value Theorem
For any three functions f, g, and h such that,
- f, g, and h are continuous in [a,b]
- f, g, and h are derivable in (a,b)
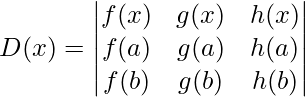
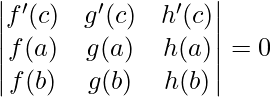
Applications of Mean Value Theorem
Mean value theorem provides a relation between a function and its derivative and this theorem is widely used in mathematical concepts. The mean value is represented as,
Let f(x) be a continuous function in the closed interval [a,b] and f(x) is differentiable on the open interval (a,b), then
f'(c) = [f(b) – f(a)]/(b-a) c ∈ (a,b)
Also, if f(b) = f(a) then,
f(c) = 0, c ∈ (a,b)
Various applications of the mean value theorem are,
- For any two functions f(x) and g(x) if they are continuous in interval [a,b] and differentiable on the interval (a,b),
f'(c) = g'(c), c ∈ (a,b), then f(x) – g(x) is constant in [a,b]
- it is used in physical interpretation (like speed analysis).
- If the derivative of the function f(x) is greater than zero then f(x) is strictly an Increasing function.
- If the derivative of the function f(x) is less than zero then f(x) is strictly a decreasing function.
- Taylor Series and Number Theory use Mean Value Theorem
Increasing and Decreasing Function
With the help of the mean value theorem, we can find whether a function is increasing or decreasing.
Increasing Function
The function y = f(x) is said to be an increasing function of x in the interval (a, b),
If the derivative of the f(x) is positive in the interval (a, b) i.e.
f'(x) > 0 for a x ∈ (a, b)
Decreasing Function
The function y = f(x) is said to be a decreasing function of x in the interval (a, b)
If the derivative of the f(x) is negative in the interval (a, b) i.e.
f'(x) < 0 for a x ∈ (a, b)
Read More,
Mean Value Theorem Examples
Example 1: f(x) = (x – 1)(x – 2)(x – 3), x ∈ [0, 4]. Find c if the Mean value theorem is applied to f(x)
Solution:
f(x) = (x – 1)(x – 2)(x – 3),
x ∈ [0, 4]
f(x) = x3 – 6x2 + 11x – 6
As f(x) is Polynomial in x
- f(x) is continuous on [0. 4]
- f(x) is differentiable on (0, 4)
Thus, all the conditions of Mean Value theorem are satisfied.
To verify theorem we have to find c ∈ (0, 4) such that
f’(c) = (f(4) – f(0))/(4 – 0) …(1)
Now, f(4) = (4 – 1)(4 – 2)(4 – 3) = 6
f(0) = (0 – 1)(0 – 2)(0 – 3) = – 6 and
f'(x) = 3x2 – 12x + 11
f'(c) = 3c2 – 12c + 11
(f(4) – f(0))/(4 – 0) = 3c2 – 12c + 11 [From 1]
3 = 3c2 – 12c + 11
3c2 – 12c + 8 = 0
c = 2 ± 2/√3
Both values of c lie between 0 and 4.
Example 2: Verify LaGrange’s mean value theorem for the function f(x) = log(x) on [1, e]
Solution:
f(x) = log(x)
f(x) is continuous on [1, e]
f(x) is differentiable on (1, e), Thus all the conditions of Mean Value theorem are satisfied.
We want to find c ∈ (1, e) such that
f(e) – f(1) = f'(c) {e – 1} … from (1) [By mean value theorem]
log e -log 1 = f'(c) {e – 1}
1 – 0 = f'(c) {e – 1}
f'(c) = 1/(e – 1) …[2]
Now,
f(x) = log(x)
Hence, f'(x) = 1/x
f'(c) = 1/c …[3]
From [2] and [3]
1/(e – 1) = 1/c
Hence,
c = e – 1 which is lies in interval (1, e)
Thus, LaGrange’s mean value theorem verified.
Example 3: Test whether the following function is increasing or not. f(x) = x3 – 3x2 + 3x – 100, x ∈ R
Solution:
f(x) = x3 – 3x2 + 3x – 100, x ∈ R
Differentating with respect to x
f'(x) = 3x2 – 6x + 3
= 3(x – 1)2
Since (x – 1)2 is always positive x ≠1
f'(x) >0, for all x ∈ R.
Hence, f(x) is an increasing function, for all x ∈ R.
Example 4: Find the value of x for which the function f(x) = x3+12x2+36x+6, x is increasing.
Solution:
f(x) = x3 + 12x2 + 36x + 6
f'(x) = 3x2 + 24x + 36 = 3(x + 2)(x + 6)
Now, f'(x) > 0, as f(x) is increasing
3(x + 2)(x + 6) > 0
The above condition is true in two cases
Case 1: Both multiples are positive
x + 2 > 0 and x + 6 > 0
x > -2 and x > -6
x ∈ (-2, ∞)
Case 2: Both multiples are negative
x + 2 < 0 and x + 6 > 0
x < -2 and x < -6
x ∈ (-∞, -6)
Thus, f(x) = x3 + 12x2 + 36x + 6 is increasing in the interval, x∈ (-∞, -6) U (-2, ∞)
Example 5: For the function f(x) = 2x3 + 2, find all the values of c that satisfy the mean value theorem, in the interval [-2, 2].
Solution:
f(x) = 2x3 + 2 is a polynomial function and hence it is continuous and differentiable over the interval [-2, 2]
f'(x) = 6x
f(2) =2(2)3 + 2 = 18
f(-2) = 2(-2)3 + 2 = -14
f'(c) = [ f(2) – f(-2)] / (2 – (-2)) = [18 – (-14)] /4 =8
Let us find c in (-2, 2) such that f'(c) = 8
f'(c) = 6c
According to Mean Value Theorem
6c = 8
c = 8/6 = 1.33
Thus, c belongs to the interval [-2, 2].
FAQs on Mean Value Theorem
Q1: State Mean value theorem.
Answer:
For any function f(x) such that f(x) is continuous in [a,b] and f(x) is differentiable in (a,b) then according to Mean Value Theorem,
There exist a c in the interval [a, b] such that,
f'(c) = [f(b)–f(a)]/(b-a)
Q2: What is Rolle’s Theorem?
Answer:
Rolle’s Theorem states that for any function f(x) such that f(x) is continuous in [a,b] and f(x) is differentiable in (a,b) then there exists a point c in the [a, b] such that the tangent at point is parallel to the x-axis.
Q3: What is the Mean Value Theorem Equation?
Answer:
The mean value theorem equation is,
f'(c) = [ f(b) – f(a) ] / (b – a)
which is applicable on f(x): [a, b]→ R such that f(x) is continuous in [a,b] and f(x) is differentiable in (a,b)
Q4: What is the Difference Between Mean Value Theorem and Intermediate Value Theorem?
Answer:
For any continuous function, f(x) is continuous on [a, b] and differentiable on (a, b),
- According to the Mean Value Theorem, there exists a ‘c’ in the interval (a, b) such that f'(c) = [ f(b) – f(a) ] / (b – a).
- According to the Intermediate Value Theorem, for any L between f(a) and f(b), there exists a ‘c’ in the interval (a, b) such that f(c) = L.
Q5: What is Mean Value Theorem Formula?
Answer:
The mean value theorem formula is,
f’(c) = [f(b) – f(a)]/(b-a)
Share your thoughts in the comments
Please Login to comment...