Vectors algebra is the branch of algebra that involves operations on vectors. Vectors are quantities that have both magnitude and direction so normal operations are not performed on the vectors. We can add, subtract, and multiply vector quantities using special vector algebra rules. Vectors can be easily represented in 2-D or 3-D spaces. Vector algebra has various applications it is used in solving various problems in mathematics and physics, engineering, and various other fields.
In this article, we will learn about vector algebra, operations in vector algebra, types of vectors, and others in detail.
What Is Vector Algebra?
Vector algebra is the type of Algebra that is used to perform various algebraic operations on vectors. As we know vectors are quantities that have both magnitude and direction whereas scalar quantities only have magnitude and no direction. The difference between vector quantities and scaler quantities can be understood with the help of the example discussed below.
The height and weight of a person can be described by a single number like 75 Kg or 150cm. These quantities only have magnitude, they do not require any extra information. Such quantities are called scalar quantities.
Now, let’s consider another situation, the coach of the football team wants to teach his goalkeeper to pass the ball to another player, now he will have to describe the region he should send the ball (Direction) and how hard he should hit (magnitude). This quantity requires both magnitude and direction. Such quantities are called vectors.
Such quantities in which direction are present are called Vector quantities. Examples of vector quantities are Displacement, Velocity, Force, etc. As these quantities have directions operations on these quantities are not easily applied and the concept of vector algebra is used to perform operations on these quantities.
In the above figure, the length of the line shows the magnitude of the vector, and the arrowhead points to its direction. It is basically a directed line segment  . Its starting point A is called the initial point and point B where it ends is called the terminal point.
. Its starting point A is called the initial point and point B where it ends is called the terminal point.
Representation of Vectors
Vectors are represented by taking an arrow above the quantity, i.e. force vector is represented as  where the arrow above F represents that it is a vector quantity. Vectors can also be represented by taking their respective magnitude in x, y, and z-directions respectively. The x-direction is shown using
where the arrow above F represents that it is a vector quantity. Vectors can also be represented by taking their respective magnitude in x, y, and z-directions respectively. The x-direction is shown using  , similarly, the y-direction is shown using
, similarly, the y-direction is shown using  and the z-direction is shown using
and the z-direction is shown using  . Now the vector A is represented as,
. Now the vector A is represented as,
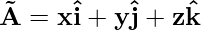
The point where the vector start is called the tail of the vector and the endpoint of the vector is called the head of the vector. We can also denote the vector as the coordinate point in 3-Dimensions.
The basis vectors are denoted as
- e1 = (1,0,0)
- e2 = (0,1,0)
- e3 = (0,0,1)
Magnitude of Vectors
The magnitude of a vector represents the strength of the vector. We can calculate the magnitude of the vector by taking the square root of the sum of the squares of each component in the x, y, and z directions.
The magnitude of a vector is calculated by taking the square root of the sum of the square of the components of the vector in the x, y, and z directions.
For any vector  , the magnitude of the vector is represented as |A| and its value is
, the magnitude of the vector is represented as |A| and its value is
|A| = √ (a2+b2+c2)
The magnitude of a vector is a scalar value.
Components of Vectors
A vector can be easily broken into its two components which represent the value of the vector in perpendicular dimensions. In a 2-D coordinate system, we can easily break the vector into two components namely the x-component and y-component.
For any vector 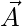 its,
its,
- x-components is Ax and its value is Ax = Acosθ
- Y-components is Ay and its value is Ay = Asinθ
where θ is the angle formed by the vector with the positive x-axis. Also, the magnitude of the vector A is calculated using the formula,
|A| = √[(Ax)2 +(Ay)2]
Angle Between Two Vectors
If two vectors in the 2-D plane intersect each other then the angle between them can easily be calculated using the dot product of the vector formula. We know that for two vectors vector a, and vector b their dot product is given by,
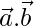 = |a|.|b|. cos θ
= |a|.|b|. cos θ
We can easily calculate the dot product of the two vectors using the dot product rule and then taking the inverse trigonometric cos function on both sides we can easily calculate the angle between two vectors as,
θ = cos-1[(a·b)/|a||b|]
Types of Vectors
Vectors can be classified into different categories on the basis of their magnitude and direction. The various types of vectors are listed below:
- Zero Vector
- Unit Vector
- Equal Vector
- Negative Vector
- Co-Initial Vectors
- Collinear Vectors
- Parallel Vectors
- Orthogonal Vectors
Let’s discuss these types of vectors in detail.
Zero Vector
A vector whose initial and terminal points coincide is called a zero vector. It cannot be assigned any direction or magnitude. The magnitude of the zero vector is 0. In the coordinate system, we write the zero vector as (0, 0, 0). The additive identity of the vector is zero vector, i.e.
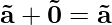
Unit Vector
A vector that has a unit magnitude is called the unit vector. A unit vector in the direction of given vector 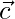 is denoted by
is denoted by 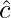 and is given by:
and is given by:

Equal Vector
Two vectors are considered equal if they have the same direction and magnitude. They have equal components in respective directions but they can have different initial and final points.
Negative Vector
A vector is called the negative vector of a vector if it has the same magnitude as the original vector but the direction is opposite to the original vector. For any vector A the negative vector is – A.
The above four vectors are shown in the image added below,
Co-Initial Vectors
The vectors which start from the same point are called co-initial vectors.
Collinear Vectors
Two vectors are said to be collinear if they are parallel to the same line, irrespective of their magnitudes and direction.
Parallel Vectors
If the angle between two vectors is zero then the vectors are called parallel vectors. They have similar directions but the magnitude may or may not be the same.
Orthogonal Vectors
If the angle between two vectors is a right angle, i.e. 90 degrees then the vectors are called orthogonal vectors. The dot product of the orthogonal vector is always zero.
The above four vectors are shown in the image added below,
Operations in Vector Algebra
We can perform various operations in Vector Algebra by taking a geometrical approach or by taking a coordinate system approach. Various operations in vector algebra are,
- Addition of Vectors
- Subtraction of Vectors
- Multiplication of Vectors by Scalar
- Scalar Triple Product of Vectors
- Multiplication of Vectors
Now we will understand each of these operations in vector algebra below in the article.
Addition of Vectors
A vector  can be thought of as a displacement from point A to point B. To understand the need for the addition and subtraction of vectors, consider an example. In the figure, Laxmi goes from point A to point B and then to point C following the vectors shown in the figure. Now, after reaching point C, the net displacement made by this girl is from A to C which is given by the vector
can be thought of as a displacement from point A to point B. To understand the need for the addition and subtraction of vectors, consider an example. In the figure, Laxmi goes from point A to point B and then to point C following the vectors shown in the figure. Now, after reaching point C, the net displacement made by this girl is from A to C which is given by the vector  .
.
This can be expressed in terms of vectors as,

This is known as the triangle law of vector addition.
Triangle Law of Vector Addition
The triangle law of vector addition states that if two sides of any triangle represent the two vectors that are on a body in the same order as the side of the triangle, then the third side of the triangle represents the resultant vector.
In general, for two vectors  and
and  their addition is done such that the initial point of one vector coincides with the terminal points of the other.
their addition is done such that the initial point of one vector coincides with the terminal points of the other.
In the figure, we have two vectors a and b given
Now the vector b is shifted without changing its direction and magnitude such that now the initial point of vector  lies on the endpoint of vector a as shown in the figure,
lies on the endpoint of vector a as shown in the figure,
In the case of subtraction, the direction of vector b is reversed, and then both vectors are added as shown in the image below,
Parallelogram Law of Vector Addition
Parallelogram law of vector addition states that if the adjacent side of the parallelogram represents two vectors then the diagonal starting from the same initial point represents the resultant of the vector.
Properties of Vector Addition
Various properties of vector addition are
Property 1: Vector addition follows commutative property. For two vectors  and
and  .
.
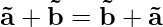
Property 2: Vector addition of three vectors follows the associative property.
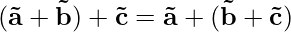
Subtraction Of Vectors
Subtraction Of Vectors is similar to the addition of the vector only the director of the vector which is to be subtracted is reversed and then the addition of the vector is calculated using the vector addition formulas.
Suppose we have to find the subtraction of two vectors say A and B then this condition is represented as, A – B. Now we know that the subtraction is calculated by reversing the subtracted vector and then adding then both as,

Multiplication of Vectors by Scalar
Let’s say  is a given vector and “k” be a scalar. The product of the scalar will either increase or decrease the magnitude of the vector. The direction of the vector will remain the same. The increase or decrease in the magnitude of the vector will depend upon the value of the scalar that is multiplied by the vector. The figure below shows vector A multiplied by some scalar quantity. Notice how the length of the vector changes after being multiplied by a scalar.
is a given vector and “k” be a scalar. The product of the scalar will either increase or decrease the magnitude of the vector. The direction of the vector will remain the same. The increase or decrease in the magnitude of the vector will depend upon the value of the scalar that is multiplied by the vector. The figure below shows vector A multiplied by some scalar quantity. Notice how the length of the vector changes after being multiplied by a scalar.
The magnitude of the vector will become,
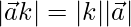
When k = -1, the direction of the vector is reversed,
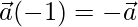
This is called the additive inverse of the vector.
Multiplication of Vectors
Multiplication of two vectors is achieved in two ways
- Dot Product: In dot product, the resultant is a scaler quantity.
- Cross Product: In cross product, the resultant is a vector quantity.
Now let’s learn about them in detail.
Dot Product of Vectors
The dot product is also called the scalar product. The dot product of the two vectors is denoted by dot(.) between those two vectors. The dot product of two vectors results in the scaler quantity and hence it is also called the scalar product. Suppose we take two vectors P and Q then their dot product is calculated using the formula,
P.Q = |P| |Q| cos θ
If both the vectors P and Q are parallel, i.e. angle between them (θ) = 0°, then
P.Q = |P| |Q|
If both the vectors P and Q are orthogonal, i.e. angle between them (θ) = 90°, then
P.Q = 0 (cos 90° = 0)
If the coordinates of the two vectors P and Q are given in Vector Algebra then,
P = [P1,P2,P3,….,Pn] and Q = [Q1,Q2,Q3,….,Qn]
Now the dot product of P and Q is given by the formula,
P.Q = P1Q1 + P2Q2 + P3Q3 + ……….PnQn
Cross Product of Vectors
The cross product between two vectors is denoted by the multiplication sign(×) between two vectors. The cross product of two vectors results in a vector quantity. It is defined only in the 3-Dimensional coordinate system.
For any vectors P and Q, the cross-product is represented as P × Q and is calculated using the formula,
P × Q = |P| |Q| sin θ
In the coordinate system, the cross product of two vectors is defined as,
Learn more about Vector Operations
Vector Algebra Formulas
We use various formulas in Vector Algebra to solve various types of complex problems. These formulas are very helpful in understanding and solving vector algebra problems. The important vector algebra formulas are,
- (ai + bj + ck) + (pi + qj + rk) = (a+p)i + (b+q)j + (c+r)k
- (ai + bj + ck) – (pi + qj + rk) = (a-p)i + (b-q)j + (c-r)k
- (ai + bj + ck) . (pi + qj + rk) = (a.p)i + (b.q)j + (c.r)k
If vector A = ai + bj + ck and vector B = pi + qj + rk, then
- A × B = (br – cq)i + (ar – cp)j + (aq – bp)k
The angle between two vectors is given as,
Associative Property of Multiplication
- A.B = B.A
- A × B ≠ B × A
- A × B = -B × A
Other Properties
- i.i = j.j = k.k = 1
- i.j = j.k = k.i = 0
- i×j = k
- j×k = i
- k×i = j
Applications of Vector Algebra
Vector algebra is widely used in various fields such as Mathematics, Engineering, Physics, and others. Various physical quantities encountered by us in real life such as force, acceleration, velocity, and others are vector quantities and we use vector algebra to define and operate on those quantities. Some of the important applications of vector algebra are
- Vector algebra is used to study electromagnetic fields, gravitational fields, fluid flow, and other topics in engineering and physics.
- Differential Equation and Partial Differential Equations are solved using vector algebra.
- The resultant of the force acting on the body is calculated using vector algebra.
- Vector Algebra is used to find equipotential surfaces.
Read More,
Vector Algebra Examples
Example 1: Find the dot product of vectors P(a, b, c) and Q(p, q, r).
Solution:
We know that dot product of the vector is calculated by the formula,
P.Q = P1Q1+P2Q2+……….PnQn
Thus,
P.Q = a.p + b.q + c.r
The dot product of vector P and vector Q is ap + bq + cr
Example 2: Find the dot product of vectors P(1, 3, -5) and Q(7, -6, -2).
Solution:
We know that dot product of the vector is calculated by the formula,
P.Q = P1Q1+P2Q2+……….PnQn
Thus,
P.Q = 1.7 + 3.(-6) + (-5).(-2)
⇒ P.Q = 7 – 18 + 10
⇒ P.Q = 17 – 18
⇒ P.Q = -1
The dot product of vector P and vector Q is -1
Example 3: Let’s say two vectors are defined as  and
and  . Find,
. Find, 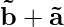
Solution:
Given,
 ….(1)
….(1)
 ….(2)
….(2)
Now, let’s calcualte  +
+ 
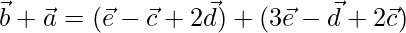
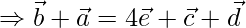
Example 4: Find the magnitude of the vector A = 2i – 5j + 4k, using vector algebra.
Solution:
Given Vector,
Vector A = 2i – 5j + 4k
We know that magnitude of the vector A is |A| i.e.
|A| = √ (a2+b2+c2)
⇒ |A| = √ (22+(-5)2+42)
⇒ |A| = √(4 + 25 + 16)
⇒ |A| = √(45) = 3√(5)
FAQs on Vector Algebra
Q1: What is Vector Algebra?
Answer:
As we know that vectors are quantities that have both magnitude and direction. So it is not easy to directly apply mathematical operations to them, the algebra which deals with the vector is called vector algebra.
Q2: What is Vector?
Answer:
Every quantity in math and physics is categorised into two basic categories Scaler and Vector. A vector is that quantity which have both magnitude and directions.
Q3: What are the Uses of Vector Algebra?
Answer:
Vector Algebra is widely used in various fields such as,
- Vector algebra is used to study electromagnetic fields, gravitational fields, fluid flow, and other topics in engineering and physics.
- Differential Equation and Partial Differential Equations are solved using vector algebra., etc
Q4: What are the Properties of Vectors in Vector Algebra?
Answer:
Various properties of vectors in vector algebra are,
- A.B = B.A
- A × B ≠ B × A
- A × B = -B × A
Q5: What is the condition for two vectors to be perpendicular?
Answer:
Two vectors are said to be perpendicular if the angle between them is 90 degrees. Perpendicular vectors are also called orthogonal vectors. The condition for two vectors to be perpendicular is that the dot product of the two vectors is zero.
We can say that two vectors A, and B are perpendicular if,
A.B = 0
Like Article
Suggest improvement
Share your thoughts in the comments
Please Login to comment...