Vector Operations

Vector Operations are operations that are performed on vector quantities. Vector quantities are the quantities that have both magnitude and direction. So performing mathematical operations on them directly is not possible. So we have special operations that work only with vector quantities and hence the name, vector operations.

Thus, It is essential to know what kind of operations can be performed on the vector quantities and vector operations tells us about the same. This article deals with vector operations, such as vector addition, the cross product of two vectors, the dot product of two vectors, and others in detail. Let’s learn about all of them in detail, here in this article.

Operations on Vectors

Operations on vectors are the vectors that are performed especially on vector quantities, such quantities have both magnitude and direction, and operating them with normal rules of mathematics is not possible. So we have to use various vector operations that include,

• Addition of Two Vectors
• Subtraction of Two Vectors
• Multiplication of Vector with Scalar
• Product of Two Vectors
  • Dot Product
  • Cross-Product

Addition of Vectors

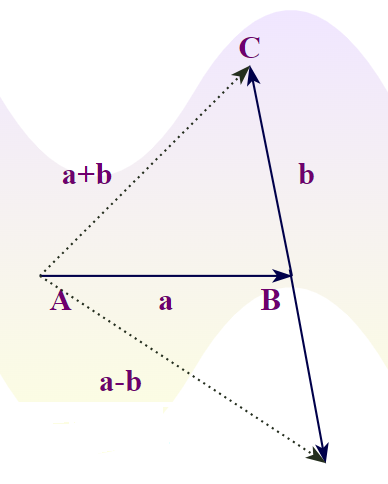
Vectors cannot be added by usual algebraic rules. While adding two vectors, the magnitude and the direction of the vectors must be taken into account. Triangle law is used to add two vectors, the diagram below shows two vectors “a” and “b” and the resultant calculated after their addition. Vector addition follows commutative property, this means that the resultant vector is independent of the order in which the two vectors are added. 

\vec{a} + \vec{b} = \vec{c}

The commutative property of vector addition states that,

\vec{a} + \vec{b} = \vec{b} + \vec{a}

Triangle Law of Vector Addition

Consider the vectors given in the figure above. The line AB represents the vector “a”, and BC represents the vector “b”. The line AC represents the resultant vector. The direction of AC is from A to C.

Line AC represents, 

\vec{a} + \vec{b}

The magnitude of the resultant vector is given by, 

\sqrt{|a|^2 + |b|^2 + 2|a||b|cos(\theta)}

The θ represents the angle between the two vectors. Let Φ be the angle made by the resultant vector with the vector p.

tan(\phi) = \frac{qsin(\theta)}{p + qcos(\theta)}

Parallelogram Law of Vector Addition

According to Parallelogram Law of Vector Addition if, “Adjacent side of a parallelogram represents two vectors then the diagonal starting from the same initial point represents the resultant of the vector.”

This is represented as by the image added below:

Here, vector A and vector B represents the sides of parallelogram PQ and QR respectively and QS represents the resultant sum vector C.

Subtraction of Two Vectors

Two vectors can be easily subtracted using the vector addition rules. A negative vector is considered a vector with opposite direction so it is easily solved by reversing its direction and applying Trinagle Law of Vector Addition.

Two vectors a and b are subtracted easily as shown in the image added below:

Multiplication of Vectors with Scalar

Multiplying a vector a with a constant scalar k gives a vector whose direction is the same but the magnitude is changed by a factor of k. The figure shows the vector after and before it is multiplied by the constant k. In mathematical terms, this can be rewritten as, 

|k\vec{a}|~=~k|\vec{a}|

if k > 1, the magnitude of the vector increase while it decreases when the k < 1. The image added below shows the scaler multiplication of vec a with a scaler number k where k is any constant greater than 1. (k>1)

Product of Two Vectors

Vectors can be multiplied by each other but they cannot be divided. In the case of multiplication, there are basically two kinds of multiplication,

• Scalar Multiplication of Vector Or Dot Product
• Vector Multiplication of Vector Or Cross Product

Scalar Multiplication (also known as dot product) is a kind of multiplication that results in a scalar quantity. Vector Multiplication (also known as Cross Product) is a kind of multiplication that results in a vector quantity. Vector products are used to define other derived vector quantities. 

Dot Product Or Scalar Product of Vector

Consider two vectors \vec{A} 

and \vec{B}

. The scalar product of these two vectors is defined by the equation, 

\vec{A}\cdot \vec{B} = |\vec{A}||\vec{B}|cos(\theta)

Here, θ is the angle between two vectors.

In case the vectors are given by their components. for example a = a₁i + a₂j + a₃k and b = b₁i + b₂j + b₃k. In this case, the dot product is given by, 

a.b = a₁b₁i + a₂b₂j + a₃b₃k

Vector Product Or Cross Product of Vectors

Consider two vectors \vec{A} and \vec{B} . The vector product of these two vectors is denoted by  \vec{A} \times \vec{B}

 . The direction of this vector is perpendicular to both of the vectors. The magnitude of this vector is given by, 

|\vec{A} \times \vec{B}| = |\vec{A}||\vec{B}|sin(\theta)

Here, θ is the angle between two vectors. 

The right-hand rule is used to determine the direction of the resulting vector from the cross-product. Note that unlike the addition and dot product, the vector product is not commutative in nature. 

In case the vectors are given by their components. for example a = a₁i + a₂j + a₃k and b = b₁i + b₂j + b₃k. In this case, the cross product is given by,

\vec{A} \times \vec{B} = \begin{vmatrix} \hat{i} & \hat{j} & \hat{k} \\ a_1 & a_2 & a_3 \\ b_1 & b_2 & b_3 \end{vmatrix} \\ 

Read More,

• Vector Algebra
• Scalars and Vectors
• Scalar Product of Vectors

Problems on Vector Operations

Problem 1: A vector is given by, v = 2i + j. Find the magnitude of the vector when it is scaled by a constant of 0.4. 

Solution:

For any vector (v) = ai + bj, its magnitude is given as

|v| = \sqrt{a^2 + b^2}

0.4|v| = |0.4v| 

a = 2, b = 1

|0.4v|

&#x21d2 |0.4(2i + j)| 

&#x21d2 |0.8i + 0.4j| 

|v| = \sqrt{0.8^2 + 0.4^2}

&#x21d2 |v| = \sqrt{0.64 + 0.16}

&#x21d2 |v| = ????.8

Problem 2: Two vectors with magnitude 5 and 10. These vectors have a 60° angle between them. Find the magnitude of the resultant vectors. 

Solution:

Let, two vectors be p and q. Then resultant vector “r” is given by, 

|r| = \sqrt{|p|^2 + |q|^2 + 2|p||q|cos(\theta)}

Given,

• |p| = 5
• |q| = 10
• θ = 60^o

|r| = \sqrt{|p|^2 + |q|^2 + 2|p||q|cos(\theta)}

&#x21d2 |r| = \sqrt{|5|^2 + |10|^2 + 2|5||10|cos(60)}

&#x21d2 |r| = \sqrt{|5|^2 + |10|^2 + (10)(5)}

&#x21d2 |r| = \sqrt{25 + 100 + 50}

&#x21d2 |r| = &#x221a(175)

The magnitude of resultant vector is |r| = 5&#x221a(7)

Problem 3: Two vectors with magnitude 4 and 4. These vectors have a 60° angle between them. Find the magnitude of the resultant vectors and the angle made by the resultant vector. 

Solution:

Let, two vectors be p and q. Then resultant vector “r” is given by, 

|r| = \sqrt{|p|^2 + |q|^2 + 2|p||q|cos(\theta)}

• |p| = 4
• |q| = 4
• θ = 60^o

|r| = \sqrt{|p|^2 + |q|^2 + 2|p||q|cos(\theta)}

&#x21d2 |r| = \sqrt{|4|^2 + |4|^2 + 2|4||4|cos(60)}

&#x21d2 |r| = \sqrt{16 + 16 + 2|4||4|cos(60)}

&#x21d2 |r| = \sqrt{48}

&#x21d2 |r| = 4????

Angle made by resultant, 

tan(\phi) = \frac{4sin(60)}{4 + 4cos(60)}

&#x21d2 tan(\phi) = \frac{2\sqrt{2}}{4 + 2}

&#x21d2tan(\phi) = \frac{\sqrt{2}}{3}

&#x21d2 Φ = tan^-1(2/3)

Problem 4: Two vectors are given by, a = 2i + j + k and b = i + j + k. Find the dot product of these two vectors. 

Solution:

Given,

• a = 2i + j + k 
• b = i + j + k 

Dot Product = a.b 

&#x21d2 (2i + j + k ).(i + j + k)

&#x21d2 2.1  + 1.1 + 1.1 

&#x21d2 4 

Problem 5: Two vectors are given by, a = 2i + j + k and b = i + j + k. Find the cross product of these two vectors. 

Solution:

Given,

• a = 2i + j + k 
• b = i + j + k 

Cross Prodcut of Vector = (2i + j + k) × (i + j + k)

\vec{A} \times \vec{B} = \begin{vmatrix} \hat{i} & \hat{j} & \hat{k} \\ 2 & 1 & 1 \\ 1 & 1 & 1 \end{vmatrix} \\ = \hat{i}\begin{vmatrix} 1 & 1 \\ 1 & 1 \end{vmatrix} – \hat{j}\begin{vmatrix} 2 & 1 \\ 1 & 1 \end{vmatrix} + \hat{k}\begin{vmatrix} 2 & 1 \\ 1 & 1 \end{vmatrix} \\ = -\hat{j}(2.1 – 1.1) + \hat{k}(2.1 – 1.1) \\ = -\hat{j} + \hat{k}

FAQs on Vector Operations

1. What are Vector Operation?

Vector operations are the mathematical operation performed on vector quantities. Some of the important vector operation include,

• Vector Addition
• Vector Multiplication
  • Cross Product of Vectors
  • Dot Product of Vector

2. What is Triangle Law of Vector Addition?

Triangle Law of Vector Addition is the basic law that gives the sum of two vectors. It states that if two vectors are represented using two sides of a triangle then the third side of triangle represent the sum of these two vectors.

3. What is Parallelogram Law of Vector Addition?

Parallelogram Law of Vector Addition is the basic law that gives the sum of two vectors. It states that if two vectors are represented using two adjacent sides of a paralllelogram then the diagonal of the parallelogram represent the sum of these two vectors.

4. What is Cross Product of Two Vectors?

Cross Product of Two Vectors is also called the vector multiplication of two vectors, it is denoted using (×) symbol. The result of cross product of two vector is a vector quantity.

5. What is Dot Products of Two Vectors?

Doy Product of Two Vectors is also called the scaler multiplication of two vectors, it is denoted using (.) symbol. The result of dot product of two vector is a scaler quantity.