Minors and Cofactors are important to calculate the adjoint and inverse of a matrix. As the name suggests, a Minor is a smaller part of the larger matrix obtained for a particular element of the matrix by deleting the terms of the row and column to which the element belongs. Cofactor is (-1)i+j times the minor of the matrix. They are the backbones of Linear Algebra and are used to find the value of the determinant, adjoint, and inverse of a matrix. Other than that there are many use cases in computer science for minors and cofactors. In this article, we will study minors and cofactors in detail. Other than that, we will also learn about the determinants, matrix inversion, and many more.
What is the Determinant of a Matrix?
Determinant is useful for solving linear equations, capturing how linear transformation change area or volume, and changing variables in integrals. The determinant can be viewed as a function whose input is a square matrix and whose output is a number. In simple language we can say, to every small matrix A, we can associate a number (real or complex) which is called the determinant of a square matrix A.
The determinant of a matrix A can be easily represented as det(A) or |A|.
.png)
Minor of a Matrix
Minor of an element aij of a determinant is a determinant obtained by deleting the ith row and jth column in which element aij lies. Minor of an element aij is denoted by Mij
How to Find Minor of a Matrix?
Use the following steps to find the minor of any given matrix:
Step 1: Hide the ith row and jth column of the matrix A, where the element aij lies.
Step 2: Now compute the determinant of the matrix after the row and column is removed using step 1.
Step 3: Result of Step 2 is the minor for he elelment of the ith row and jth column, then repeat the process for each element of the matrix to find the minor for all the elements of the matrix.
Sample Problems on Minor of a Matrix
Problem 1: If the matrix [Tex] \bold{A = \begin{bmatrix} 1&2&3\\ 2&0&1\\ 5&3&6 \end{bmatrix}}
[/Tex] then find the minor of a22.
Solution:
In this question, we have to find out the minor of a22, the element present at a22 is 0. As we learn from our definition of a minor we have to delete the ith row and jth columns at which our asked element is present. Below image is demonstrating how to delete the ith row and jth column
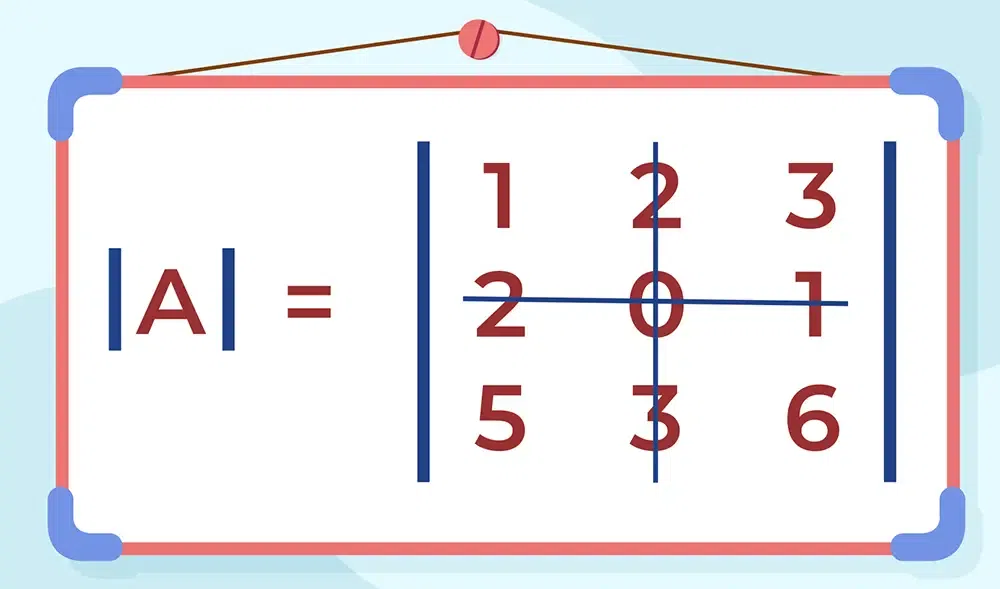
After deletion, we write our left element as it is and do cross multiplication.
Minor of element a22 =[Tex] \begin{vmatrix} 1&3\\ 5& 6 \end{vmatrix}
[/Tex]
⇒ Minor of element a22 = 6 – 15 = -9
Note: Always remember, after the multiplication of the left diagonal element in the second-dimensional determinant, always put the -ve sign then do the multiplication of right diagonal elements and solve them out.
Problem 2: If the matrix [Tex]\bold{A = \begin{bmatrix} 1 & 0 & 4\\ 3 & 5 &-1\\ 0 & 1 & 2 \end{bmatrix}}
[/Tex], then find the minor of a32.
Solution:
In the above question we have asked to find out the minor of a32 element which is 1. So as we did in this above problem same procedure we will follow. So firstly we have to delete the ith row and jth column at which our element is present.

So we had canceled the ith row and jth column at which our element is present. So write the elements which are left as it is.
Then do the cross multiplication and solve:
Minor of element a32 =[Tex] \begin{vmatrix} 1&4\\ 3& -1 \end{vmatrix}
[/Tex]
Minor of element a32 = -1 -12 = -13
Cofactor of a Matrix
Co-factor of an element aij of a determinant, denoted by Aij or Cij, and is defined as follows:
Cij = (-1)i+j Mij
Where,
- Mij is the minor of the element aij, and
- i and j respectively reprensent the number of row and column of the element (position).
Sample Problems on Cofactors of a Matrix
Problem 1: If a matrix A is [Tex]\bold{|A| = \begin{vmatrix} 5&3&1\\ 2&0&-1\\1&2&3 \end{vmatrix}}
[/Tex]write the cofactor of the element a32.
Solution:
As asked in question we have to find the co factor of element a32 which means our row (i) = 3 and column (j) = 2 so we have row and column as we do to find the minor by deleting the rows and column at which asked element exist we do the same in this question to and then put that in our formula -> Aij = (-1)i+j Mij
Cofactor of elements [Tex]= (-1)^{3+2}\begin{vmatrix}5 & 1\\2&-1 \end{vmatrix}[/Tex]
⇒ Cofactor of element = (-1)(-5 – 2) = 7
So after putting in the formula of finding cofactor and doing expansion of determinant we get (-1) (-5 – 2) which on solving gives the answer 7, this is our required answer.
Problem 2: If Aij of the element aij of the determinant is given below, then write the value of a32 . A32.
[Tex] \bold{|A| = \begin{vmatrix} 2&-3&5\\ 6&0&4\\1&5&-7 \end{vmatrix}}
[/Tex]
Solution:
In the question, we are having determinant. So we have row and column given in the question.
Here, a32 = 5 (second element of third row)
Given, Aij is the cofactor of the element aij of A . So now we can solve this question by putting the values in the formula of cofactor as discussed in above question.
Cofactor of elements (A32)[Tex]= (-1)^{3+2}\begin{vmatrix}2 &5\\6&4 \end{vmatrix}
[/Tex]
⇒ Cofactor of element (A32) = (-1)(8 – 30) = 22
a32 . A32 = 5 . 22 = 110
So, 110 is our required answer.
Application of Minors and Cofactors
Minors and Cofactors are used in the calculation of the following terms:
Adjoint of Matrix
To calculate the adjoint of Matrix, you need to follow the following steps:
Step 1: Calculate the cofactors of each element of a given matrix.
Step 2: Construct the matrix from the cofactor of elements.
Step 3: Calculate the Transpose of the resultant matrix in Step 2.
Step 4: Resulting matrix of Step 3 is the adjoint of the given matrix.
Example: Find the adjoint of the following matrix A;
[Tex]\bold{A = \begin{bmatrix} 1&2&3\\ 4 &5 &6\\ 7&8&9 \end{bmatrix}}
[/Tex]
Solution:
Step 1: Compute the cofactors of each element in A.
C11 = 5 × 9 – 6 × 8 = -3
C12 = -(4 × 9 – 6 × 7) = 6
C13 = 4 × 8 – 5 × 7 = -3
C21 = -(2 × 9 – 3 × 8) = 6
C22 = 1 × 9 – 3 × 7 = -6
C23 = -(1 × 8 – 2 × 7) = 3
C31 = 2 × 6 – 3 × 5 = -3
C32 = -(1 × 6 – 3 × 4) = 6
C33 = 1 × 5 – 2 × 4 = -3
Step 2: Construct the matrix of cofactors.
Matrix of cofactors, [Tex]C = \begin{bmatrix} -3&6&-3\\ 6&-6&3\\ -3&6&-3 \end{bmatrix}
[/Tex]
Step 3: Transpose the matrix of cofactors.
[Tex]C’ = \begin{bmatrix} -3&6&-3\\ 6&-6&6\\ -3&3&-3 \end{bmatrix}
[/Tex]
Step 4: The resulting matrix is the adjoint of A.
[Tex]adj(A) = C’ = \begin{bmatrix} -3&6&-3\\ 6&-6&6\\ -3&3&-3 \end{bmatrix}
[/Tex]
Inverse of Matrix
To calculate the inverse of a matrix, you can use the following steps:
Step 1: Calculate the determinant of the given matrix.
Step 2: If the value of the determinant is zero, then the matrix has no inverse. Otherwise, calculate the adjoint of the matrix using the steps mentioned in the previous heading.
Step 3: Use the formula [Tex]A^{-1} = \frac{adj(A)}{|A|}
[/Tex], to calculate the inverse of the given matrix.
Example: Find the inverse of the following matrix A:
[Tex]\bold{A = \begin{bmatrix} 2&-1&0\\ -1 &2 &-1\\ 0&-1&2 \end{bmatrix}}
[/Tex]
Solution:
Step 1: Find the determinant of A.
det(A) = 2(2 × 2 – (-1) × (-1)) – (-1)((-1) ×2 – (-1) ×0) + 0
⇒ det(A) = 6 – 2 = 4
Step 2: Calculate the adjoint of A using the steps mentioned in the previous example.
C11 = 4 – 1 = 3
C12 = -(-2 – 0) = 2
C13 = 1 – 0 = 1
C21 = -(-2 – 0) = 2
C22 = 4 – 0 = 4
C23 = -(-2 – 0) = 2
C31 = (1 – 0) = 1
C32 = -(-2 – 0) = 2
C33 = 4 – 1 = 3
Matrix of cofactors,
[Tex]C = \begin{bmatrix} 3&2&1\\ 2&4&2\\ 1&2&3 \end{bmatrix}
[/Tex]
Transpose of matrix of cofactors,
[Tex]adj(A) = C’ = \begin{bmatrix} 3&2&1\\ 2&4&2\\ 1&2&3 \end{bmatrix}
[/Tex]
Step 3: Multiply the adjoint of A by the reciprocal of the determinant.
[Tex] A^{-1} = \frac{adj(A)}{4} = \frac{1}{4} \times\begin{bmatrix} 3&2&1\\ 2&4&2\\ 1&2&3 \end{bmatrix}
[/Tex]
[Tex]\Rightarrow A^{-1}= \begin{bmatrix} \frac{3}{4}&\frac{2}{4}&\frac{1}{4}\\ \frac{2}{4}&\frac{4}{4}&\frac{2}{4}\\ \frac{1}{4}&\frac{2}{4}&\frac{3}{4} \end{bmatrix}
[/Tex]
[Tex]\Rightarrow A^{-1}= \begin{bmatrix} \frac{3}{4}&\frac{1}{2}&\frac{1}{4}\\ \frac{1}{2}&1&\frac{1}{2}\\ \frac{1}{4}&\frac{1}{2}&\frac{3}{4} \end{bmatrix}
[/Tex]
Read More,
FAQs on Minors and Cofactors
Q1: What is a Minor in Matrix Algebra?
Answer:
In matrix algebra, a minor refers to the determinant of a smaller matrix obtained by deleting one or more rows and columns from a larger matrix.
Q2: What is a Cofactor in Matrix Algebra?
Answer:
In matrix algebra, the cofactor of an element in a matrix is defined as the signed minor obtained by deleting the row and column containing that element, and multiplying the resulting determinant by -1 if the sum of the row and column indices is odd.
Q3: What is the Relationship between Minors and Cofactors?
Answer:
The cofactor of an element in a matrix is equal to the product of the minor of that element and (-1)^(i+j), where i and j are the row and column indices of the element, respectively.
Q4: What is the use of Minors and Cofactors in Matrix?
Answer:
Minors and cofactors are used in the computation of the inverse of a matrix, as well as in the calculation of determinants and solutions to systems of linear equations.
Q5: How are Minors and Cofactors used to calculate the Inverse of a Matrix?
Answer:
To calculate the inverse of a matrix we first need to calculate the cofactor matrix of any given matrix, then transpose of cofactor matrix is called adjoint. Then dividing adjoint by determinant to get the inverse of the matrix.
Q6: Can Minors and Cofactors be used to solve systems of Linear Equations?
Answer:
Yes, minors and cofactors can be used to solve systems of linear equations by representing the system in the form of a matrix and using Cramer’s rule, which expresses the solution in terms of determinants of smaller matrices obtained by replacing one column of the coefficient matrix with the constant terms of the system.
Q7: What is Laplace’s Expansion Formula?
Answer:
Laplace’s expansion formula is a method for computing the determinant of a matrix by summing the products of the elements in any row or column with their corresponding cofactors. It is given as [Tex]det(A) = \sum_{j =1}^{n}(-1)^{i+j}b_{i,j}m_{i,j}
[/Tex]
Like Article
Suggest improvement
Share your thoughts in the comments
Please Login to comment...