Probability Theory: Probability is defined as the chance of happening or occurrences of an event. Generally, the possibility of analyzing the occurrence of any event concerning previous data is called probability. For example, if a fair coin is tossed, what is the chance that it lands on the head? These types of questions are answered under probability.
Probability measures the likelihood of an event’s occurrence. In situations where the outcome of an event is uncertain, we discuss the probability of specific outcomes to understand their chances of happening. The study of events influenced by probability falls under the domain of statistics.
In this article, we will learn about, Probability theory, its formulas, examples, applications, and others in detail.
What is Probability Theory in Maths?
Probability theory uses the concept of random variables and probability distribution to find the outcome of any situation. Probability theory is an advanced branch of mathematics that deals with the odds and statistics of an event.
Real-Life Example of Probability: Flipping a Coin
Flipping a coin is a classic example used to illustrate basic probability principles because it embodies randomness and has a straightforward set of possible outcomes: heads or tails. Each time you flip a fair coin (one that’s not biased), there are exactly two possible outcomes, each with an equal chance of occurring. Therefore, the probability of landing on heads is 1/2, and similarly, the probability of landing on tails is also 1/2. This scenario exemplifies a simple random experiment where each outcome has an equal likelihood, making it a foundational example for teaching and understanding probability theory.
Probability Theory Definition
Probability theory studies random events and tells us about their occurrence. The two main approaches for studying probability theory are.
- Theoretical Probability
- Experimental Probability
Theoretical and Experimental Probabilities
The image given below shows the Theoretical and Experimental Probabilities and their differences.
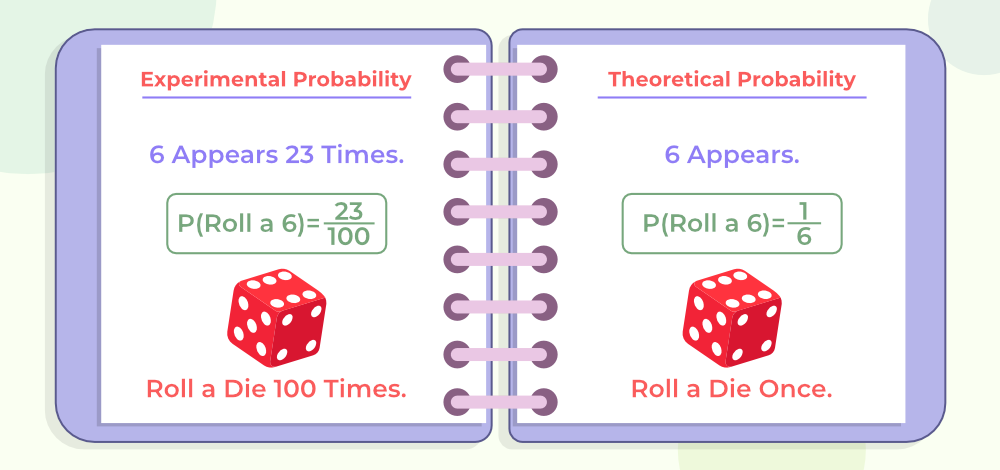
Theoretical Probability
Theoretical Probability deals with assumptions in order to avoid unfeasible or expensive repetition of experiments. The theoretical Probability for an Event A can be calculated as follows:
P(A) = (Number of outcomes favourable to Event A) / (Number of all possible outcomes)
The image shown below shows the theoretical probability formula.
.png)
Note: Here we assume the outcomes of an event as equally likely.
Now, as we learn the formula, let’s put this formula in our coin-tossing case. In tossing a coin, there are two outcomes: Head or Tail. Hence, The Probability of occurrence of Head on tossing a coin is
P(H) = 1/2
Similarly, The Probability of the occurrence of a Tail on tossing a coin is
P(T) = 1/2
The following image shows an unbiased coin that has an equal probability of landing both heads and tails

Experimental Probability
Experimental probability is found by performing a series of experiments and observing their outcomes. These random experiments are also known as trials. The experimental probability for Event A can be calculated as follows:
P(E) = (Number of times event A happened) / (Total number of trials)
The following image shows the Experimental Probability Formula,
.png)
Now, as we learn the formula, let’s put this formula in our coin-tossing case. If we tossed a coin 10 times and recorded heads for 4 times and a tail 6 times then the Probability of Occurrence of Head on tossing a coin:
P(H) = 4/10
Similarly, the Probability of Occurrence of Tails on tossing a coin:
P(T) = 6/10
Probability Theory Examples
We can study the concept of probability with the help of the example discussed below,
Example: Let’s take two random dice and roll them randomly, now the probability of getting a total of 10 is calculated.
Solution:
Total Possible events that can occur (sample space) {(1,1), (1,2),…, (1,6),…, (6,6)}. The total spaces are 36.
Now the required events, {(4,6), (5,5), (6,4)} are all which adds up to 10.
So the probability of getting a total of 10 is = 3/36 = 1/12
Basics of Probability Theory
Various terms used in probability theory are discussed below,
Random Experiment
In probability theory, any event which can be repeated multiple times and its outcome is not hampered by its repetition is called a Random Experiment. Tossing a coin, rolling dice, etc. are random experiments.
Sample Space
The set of all possible outcomes for any random experiment is called sample space. For example, throwing dice results in six outcomes, which are 1, 2, 3, 4, 5, and 6. Thus, its sample space is (1, 2, 3, 4, 5, 6)
Event
The outcome of any experiment is called an event. Various types of events used in probability theory are,
- Independent Events: The events whose outcomes are not affected by the outcomes of other future and/or past events are called independent events. For example, the output of tossing a coin in repetition is not affected by its previous outcome.
- Dependent Events: The events whose outcomes are affected by the outcome of other events are called dependent events. For example, picking oranges from a bag that contains 100 oranges without replacement.
- Mutually Exclusive Events: The events that can not occur simultaneously are called mutually exclusive events. For example, obtaining a head or a tail in tossing a coin, because both (head and tail) can not be obtained together.
- Equally likely Events: The events that have an equal chance or probability of happening are known as equally likely events. For example, observing any face in rolling dice has an equal probability of 1/6.
Random Variable
A variable that can assume the value of all possible outcomes of an experiment is called a random variable in Probability Theory. Random variables in probability theory are of two types which are discussed below,
Discrete Random Variable: Variables that can take countable values such as 0, 1, 2,… are called discrete random variables.
Continuous Random Variable: Variables that can take an infinite number of values in a given range are called continuous random variables.
There are various formulas that are used in probability theory and some of them are discussed below,
- Theoretical Probability Formula: (Number of Favourable Outcomes) / (Number of Total Outcomes)
- Empirical Probability Formula: (Number of times event A happened) / (Total number of trials)
- Addition Rule of Probability: P(A ∪ B) = P(A) + P(B) – P(A∩B)
- Complementary Rule of Probability: P(A’) = 1 – P(A)
- Independent Events: P(A∩B) = P(A) ⋅ P(B)
- Conditional Probability: P(A | B) = P(A∩B) / P(B)
- Bayes’ Theorem: P(A | B) = P(B | A) ⋅ P(A) / P(B)
Read in Detail: Bayes Theorem
Probability Theory in Statistics
Probability has various number of applications in Statistics. These are mentioned below:
- Descriptive Statistics: Probability theory helps in understanding and interpreting data summaries and distributions.
- Inferential Statistics: It forms the basis for making inferences about populations from samples, including hypothesis testing and the construction of confidence intervals.
- Regression Analysis: Probability distributions of errors are used to estimate the relationships between variables.
- Bayesian Statistics: Uses probability to represent uncertainty about the parameters of interest and updates this uncertainty as more data becomes available.
Applications of Probability Theory
Probability theory is widely used in our life, it is used to find answers to various types of questions, such as will it rain tomorrow? what is the chance of landing on the Moon? what is the chance of the evolution of humans? and others. Some of the important uses of probability theory are,
- Probability theory is used to predict the performance of stocks and bonds.
- Probability theory is used in casinos and gambling.
- Probability theory is used in weather forecasting.
- Probability theory is used in Risk mitigation.
- Probability theory is used in consumer industries to mitigate the risk of product failure.
People Also Read:
Conclusion – Probability Theory
Probability theory is a crucial branch of mathematics that analyzes the likelihood of events occurring, utilizing concepts of random variables and probability distributions to ascertain outcomes in various scenarios. It distinguishes between theoretical probability, which is based on assumptions and calculations of favorable outcomes over possible ones, and experimental probability, derived from actual experiment outcomes. For instance, flipping a coin has a theoretical probability of 1/2 for landing on heads or tails, a principle that can extend to more complex situations like rolling dice. Probability theory encompasses key terms such as random experiments, sample space, events (independent, dependent, mutually exclusive, and equally likely), and random variables (discrete and continuous). It employs formulas for calculating probabilities, including the addition rule, complementary rule, and Bayes’ theorem, integral to both descriptive and inferential statistics, regression analysis, and Bayesian statistics. Applications of probability theory span diverse fields, from predicting stock performance and weather forecasting to risk mitigation in consumer industries, underscoring its significance in daily decision-making and scientific inquiry.
Solved Examples on Probability Theory
Example 1: Consider a jar with 7 red marbles, 3 green marbles, and 4 blue marbles. What is the probability of randomly selecting a non-blue marble from the jar?
Solution:
Given,
Number of Red Marbles = 7, Number of Green Marbles = 3, Number of Blue Marbles = 4
So, Total number of possible outcomes in this case: 7 + 3 + 4 = 14
Now, Number of non-blue marbles are: 7 + 3 = 10
According to the formula of theoretical Probability we can find, P(Non-Blue) = 10/14 = 5/7
Hence, theoretical probability of selecting a non-blue marble is 5/7.
Example 2: Consider Two players, Naveena and Isha, playing a table tennis match. The probability of Naveena winning the match is 0.76. What is the probability of Isha winning the match?
Solution:
Let N and M represent the events that Naveena wins the match and Ashlesha wins the match, respectively.
The probability of Naveena’s winning P(N) = 0.62 (given)
The probability of Isha’s winning P(I) = ?
Winning of the match is an mutually exclusive event, since only one of them can win the match.
Therefore,
P(N) + P(I) =1
P(I) = 1 – P(N)
P(I) = 1 – 0.62 = 0.38
Thus, the Probability of Isha winning the match is 0.38.
Example 3: If someone takes out one card from a 52-card deck, what is the probability of the card being a heart? What is the probability of obtaining a 7-number card?
Solution:
Total number of cards in a deck = 52
Total Number of heart cards in a deck = 13
So, the probability of obtaining a heart,
P(heart) = 13/52 = 1/4
Total number of 7-number cards in a deck = 4
So, the probability of obtaining a 7-number card,
P(7-number) = 4/52 = 1/13
Example 4: Find the probability of rolling an even number when you roll a die containing the numbers 1-6. Express the probability as a fraction, decimal, ratio, or percent.
Solution:
Out of 1 to 6 number, even numbers are 2, 4, and 6.
So, Number of favorable outcomes = 3.
Total number of outcomes = 6.
Probability of obtaining an even number P(Even)= 1/2 = 0.5 = 1 : 2 = 50%
FAQs on Probability Theory
What is the concept of Probability Theory?
The branch of mathematics that deals with the odds of happening an event is called the Probability Theory. It tells us about the odds of occurring an event and also all the possible outcomes of any event.
What are the two types of probabilities in Probability Theory?
The two types of probabilities in probability theory are
- Theoretical Probability
- Experimental probability
Who invented probability theory?
The credit for the creation of modern probability theory goes to Intalian mathematics Gerolamo Cardano.
What is a random variable in Probability Theory?
A variable that describes all the possible outcomes of any random experiment is called a random variable. A random variable can either be continuous or discrete.
What are the formulas for Probability Theory?
The main formulas used in probability theory are,
- Theoretical probability: (Number of outcomes favourable to Event A) / (Number of all possible outcomes)
- Experimental Probability: (Number of times event A happened) / (Total number of trials)
Share your thoughts in the comments
Please Login to comment...