Applications of Matrices and Determinants
Last Updated :
12 Mar, 2021
One application of matrix and determinant is that it can be used to solve linear equations in two or three variables. Matrices and determinants are also used to check the consistency of any system, whether they are consistent or not.
Solution of a system of linear equation using the inverse of a matrix
The solution of a system of linear equations can be found out using the inverse of a matrix. Let the equations are:
a1x + b1y + c1z = d1
a2x r+ b2y + c2z = d2
a3x + b3y + c3z = d3
These equations can be represented using matrix as follows
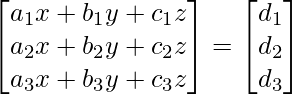
Further this can be written as
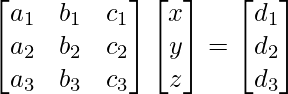
Further this system can be written as
AX = B
where matrix A is containing coefficients of unknown variables.
A = 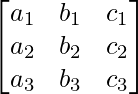
Matrix X is a column matrix that contains the unknown variables.
X = 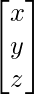
Matrix B is also a column matrix, and it contains the constants.
B = 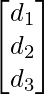
So, as given above, a system of linear equations can be converted into the form of a matrix which can be written as:
AX = B
If A is a non-singular matrix then A-1 exists.
Multiplying by A-1 on both sides
A-1AX = A-1B
IX = A-1B
X = A-1B
This provides a unique solution for the unknown variables. The solution will be unique because any non-singular matrix has a unique inverse.
If A is a singular matrix then A-1 doesn’t exist. In this case |A| = 0, so you will have to calculate (adj A)B.
1. If (adj A)B ≠ O, then any doesn’t exist for the system of linear equations, and this system will be inconsistent.
2. If (adj A)B = O, then the system of linear equations will have either zero solution or infinitely many solutions, that’s why the system may be inconsistent if it doesn’t have any solution or maybe consistent if it has infinitely many solutions.
Consistency of a system
A system of equations is said to be consistent or inconsistent based on the number of solutions it possesses.
- Consistent System: A system of equations is said to be consistent if it possesses a solution.
- Inconsistent System: A system of equations is said to be inconsistent if it doesn’t possess a solution.
Sample Problems
Question 1. Solve the following linear equations using matrix
2x + y = 3
2x + 3y = 6
Solution:
The above system of linear equations can be written in the form of AX = B where A is the matrix of coefficients, X is the matrix of unknown variables and B is the matrix of constants.
A = 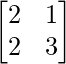
X = 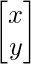
B = 
First find out the |A|
as you can see |A| = 4 ≠ 0. Hence, the system of equations is consistent and will possess an unique solution and the solution can be found out using X = A-1B
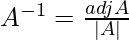
A-1 = 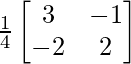
X = A-1B
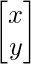 =
= 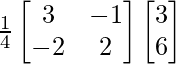
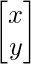 =
= 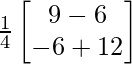
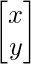 =
= 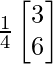
From here, you can conclude that
x = 3/4
and y = 6/4
Question 2. Say whether the given system is consistent or not
x + 3y = 5
2x + 6y = 8
Solution:
The above system of equations can be written in the form of AX = B, where
A = 
X = 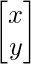
B = 
Now check determinant of A
|A| = 6 – 6 = 0g
For checking consistency of the system, you have to check (adj A)B
adj A = 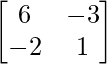
(adj A)B = 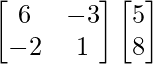
(adj A)B = 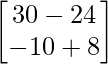
(adj A)B = 
Since (adj A)B ≠ 0, the solution of the given system of linear equations doesn’t exist. Hence, the system of equations is inconsistent.
Question 3. Solve the system of linear equations, using matrix method
x – y + 2z = 7
3x + 4y – 5z = -5
2x – y + 3z = 12
Solution:
The above system of equations can be written in the form of AX = B, where
A = 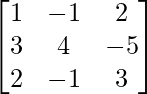
X = 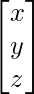
B = 
Now check determinant of A
|A| = 1 * (12 – 5) + 1 * (9 + 10) + 2 * (-3 – 8)
|A| = 7 + 19 – 22 = 4
|A| ≠ 0
Hence, its inverse exists and hence there exists a unique solution that can be found out by X = A-1B
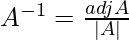
A-1 = 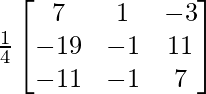
X = A-1B
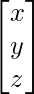 =
= 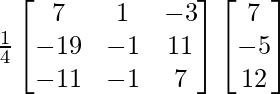
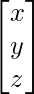 =
= 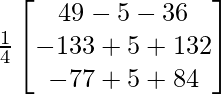
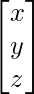 =
= 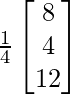
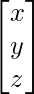 =
= 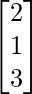
From here, you can see that x =2, y = 1, and z = 3.
Hence, x = 2, y = 1, and z = 3.
Share your thoughts in the comments
Please Login to comment...