Bernoulli Trials and Binomial Distribution are the fundament topics in the study of probability and probability distributions. Bernoulli’s Trials are those trials in probability where only two possible outcomes are Success and Failure or True and False. Due to this fact of two possible outcomes, it is also called the Binomial Trial. Binomial Distribution is the sequence of independent experiments with each experiment being a binomial trial. In this article, we are going to discuss the Bernoulli Trials in detail with the related theorems as well and also, we will study the Binomial Distribution after the understanding Bernoulli Trial.
Bernoulli’s Trials
Bernoulli’s trials are a type of experiment where you repeat the same thing over and over again independently. Each time, you’re looking for a specific outcome, which we call event A. The chance of this outcome happening is the same each time you do the experiment, no matter how many times you repeat it.
The experiment itself only has two possible outcomes, either event A happens, or it doesn’t. It’s like flipping a coin where you can either get heads or tails.
The idea of Bernoulli’s trials comes from Jacob Bernoulli, a famous mathematician from Switzerland who came up with the concept way back in the 17th century. People use Bernoulli’s trials a lot in math and statistics to understand things that happen in the real world. For example, if you wanted to figure out the odds of getting heads or tails when flipping a coin, you could use Bernoulli’s trials.
Examples of Bernoulli’s Trials
Some of the examples of Bernoulli’s trials are as follows:
- The most common example of the Bernoulli trials is flipping a coin. Each flip of the coin has only two possible outcomes: Heads and Tails. If we consider the Head to be a success, then automatically the tail becomes a failure and vice versa is also true.
- Other than this, rolling a die to get a specific number is also an example of Bernoulli’s Trials. Here if consider getting a desired number to be a success then any other outcome other than the desired number becomes a failure. In this case, each roll of the dice is a Bernoulli’s Trial.
- Checking emails: Suppose you have an inbox full of emails, and you want to check whether a particular email has arrived or not. Each time you check your inbox, you’re looking for the same event, which is the arrival of that particular email. Checking your inbox is also an example of a Bernoulli trial.
- Flipping a light switch: Suppose you have a light switch that may either turn on or off, and you want to see if it works. Each time you flip the switch, you’re conducting a Bernoulli’s trial, and you’re looking for a particular event, which is whether the light turns on or not.
Theorem Related to Bernoulli’s Trials
The following theorem gives the probability of success r number of times in n number of trials and its statement is as follows:
Statement: If the probability of occurrence of an event (probability of success) in a single trial of Bernoulli’s experiment is p, then the probability that the event occurs exactly r times out of n independent trials is equal to nCr qn – r pr, where q = 1 – p, the probability of failure of the event.
To summarize the above theorem,
Probability of r success in n Trials = nCr qn – r pr
where,
- p is the Probability of Success,
- q = 1 – p is the Probability of Failure,
- n is the Number of Independent trials, and
- r is the number of times an event occurred.
Proof:
Getting exactly r successes means getting r successes and (n – r) failures simultaneously.
∴ P(getting r successes and n – r failures) = qn – r pr (since the n trials are independent) [By Multiplication Theorem]
The trials, from which the successes are obtained, are not specified. There are nCr ways of choosing r trials for successes. Once the r trials are chosen for successes, the remaining (n – r) trials should result in failures.These nCr ways are mutually exclusive. In each of these nCr ways, P(getting exactly r successes) = qn – r pr
Therefore, by the addition theorem, the required probability = nCr qn – r pr
Binomial Distribution
Binomial Distribution is a probability distribution that describes the number of successes in a fixed number of independent binomial trials i.e., each trial can only result in either a success or a failure.
Examples of Binomial Distribution
Some examples of Binomial Distribution are as follows:
- For example, in Binomial Distribution, suppose a company sends out 1000 emails and the probability for a recipient to open that email is 0.2. Then the number of people who open the emails can be modelled by a binomial distribution with n = 100 and p = 0.2.
- Another example of this distribution includes tossing a coin. Suppose you toss a fair coin 10 times and you want to know the probability of getting exactly 5 heads. This is an example of a binomial distribution with n=10 (number of trials) and p=0.5 (probability of success).
- Let’s consider one more example of binomial distribution i.e., voting. Suppose you conduct a survey of 1000 people and ask them whether they support a certain candidate. If the probability of someone supporting the candidate is 0.6, you can model the number of people who support the candidate using a binomial distribution with n=1000 and p=0.6.
Formula for Probability in Binomial Distribution
Let A be some event associated with a random experiment E, such that P(A) = p and P(A’) = q = 1 – p. Assuming that p remains the same for all repetitions, if we consider n independent repetitions ( or trials ) of E and if the random variable (RV)X denotes the number of times the event A has occurred then X is called a binomial random variable with parameters n and p or we can say that X follows a binomial distribution with parameters n and p, or symbolically B(n, p). Obviously, the possible values that X can take, are 0, 1, 2,…., n. Then the probability mass function of a binomial random variable is given by
P(X = r) = nCr qn – r pr
Where,
- P(X = r) is the probability of getting exactly r successes,
- n is the number of total trials,
- r is the number of successes in n Trials,
- p is the probability of success,
- q is the probability of failure, and
- p + q = 1 and r = 0, 1, 2, …, n
Example: Calculate the probability of getting exactly five heads when a coin is tossed 10 times.
Solution:
As we know, P(X = k) = nCr × pr × (1-p)n-r
n = 10, r = 5, and p = 0.5
Plugging in the values, you get:
P(X = 5) = 10C5 × (0.5)5 × (1-0.5)10 – 5
⇒ P(X = 5) = 252 × 0.03125 × 0.03125
⇒ P(X = 5) = 0.24609375 ≈ 0.246
So the probability of getting exactly five heads when flipping a fair coin ten times is about 0.246, or 24.6%.
Mean and Variance of Binomial Distribution
The mean or Expected value of a binomial distribution is given by the following formula:
Mean = μ = np
and the variance or the measure of a binomial distribution is given by the following formula:
Variance = σ2 = np(1-p)
Where,
- n is the total number of Trials, and
- p is the probability of success.
Important Things to Remember about Binomial Distribution
There are some important things related to binomial distribution to which we need to pay more attention. Some of those things are as follows:
- Binomial distribution is a legitimate probability distribution since
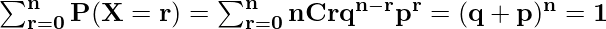
- Mean of the Binomial Distribution is given by:
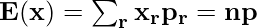
and

- Variance of the Binomial Distribution is given by:
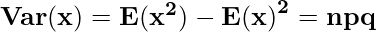
Generalization of Bernoulli’s Distribution: Multinomial Distribution
If A1, A2, . . , Ak are exhaustive and mutually exclusive events associated with a random experiment such that, P(Ai occurs) = pi where,
p1 + p2 +. . . + pk = 1, and if the experiment is repeated n times, then the probability A1 occurs r1 times, A2 occurs r2 times, . . . . , Ak occurs rk times is given by:
Pn(r1, r2, . . . , rk) = 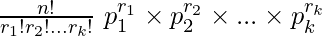
Where,
Proof:
The r1 trials in which the event A1 occurs can be chosen from the n trials nCr ways. The remaining (n – r1) trials are left over for the other events.
The r2 trials in which the event A2 occurs can be chosen from the (n – r1) trials in (n – r1)Cr2 ways.
The r3 trials in which the event A3 occurs can be chosen from the (n – r1 – r2) trials in (n – r1 – r2)Cr3 ways, and so on.
Therefore, the number of ways in which the events A1, A2, …, Ak can happen:
nCr1 × (n − r1)Cr2 × (n −r1 − r2)Cr3 × (n−r1 − r1 – …− rk − 1)Crk = n!/(r1!r2! . . . r3!)
Consider any one of the above ways in which the events A1, A2, . . ., Ak occurs.
Since the n trials are independent, r1 + r2 + . . . +rk trials are also independent.
∴ P(A1 occurs r1 times, A2 occurs r2 times, . . . , A k occurs r k times) = p1 r1 × p2r2 × . . . × pk rk
Since the ways in which the events happen are mutually exclusive, the required probability is given by
Pn (r1 , r2 , . . . , rk ) =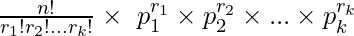
Read More,
Solved Problems of Bernoulli Trials and Binomial Distribution
Problem 1: A coin is tossed an infinite number of times. If the probability of a head in a single toss is p, show that the probability that the kth head is obtained at the nth tossing, but not earlier is (n−1)Ck−1pkqn−k, where q = 1 – p.
Solution:
K heads should be obtained at the nth tossing, but not earlier.
Therefore, (k – 1) heads must be obtained in the first (n – 1) tosses and 1 head must be obtained at the nth toss.
Required probability = P[ k – 1 heads in (n – 1) tosses] × P(1 head in 1 toss)] = (n−1)Ck−1pk-1qn−k x p
Problem 2: If at least 1 child in a family with 2 children, is a boy then what is the probability that both children are boys?
Solution:
p = Probability that a child is a boy = 1/2.
∴ q = 1 – p = 1/2 and n = 2
⇒ P (at least one boy) = p (exactly 1 boy) + p (exactly 2 boys)
⇒ P (at least one boy) = 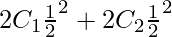
⇒ P (at least one boy) = 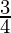
∴ Required probability = P (both are boys)/P (at least 1 boy)
⇒ Required probability = 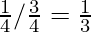
Problem 3: Out of 800 families with 4 children each, how many families would be expected to have
(i) 2 boys and 2 girls,
(ii) at least 1 boy,
(iii) at most 2 girls,
(iv) children of both sexes.
(Assume equal probabilities for boys and girls.)
Solution:
Considering each child as a trial, n = 4. Assuming that birth of a boy is a success, p = 1/2, and q = 1/2. Let X denote the number of successes(boys).
(i) P (2 boys and 2 girls) = P (X = 2)
⇒ P (X = 2) = 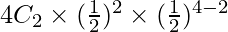
⇒ P (X = 2) 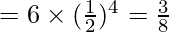
Thus, No. of families having 2 boys and 2 girls = N×P(X = 2)
[Where, N is the total no. of families considered]
⇒ Required No. of Families = 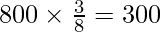
(ii) P (at least 1 boy) = P (X ≥ 1)
⇒ P (X ≥ 1) = P (X = 1) + P ( X = 2) + P (X = 3) + P (X = 4)
⇒ P (X ≥ 1) = 1 – P (X = 0)
⇒ P (X ≥ 1) = 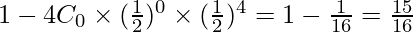
Thus, No. of families having at least 1 boy = N×P(X ≥ 1)
⇒ Required No. of Families = 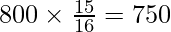
(iii) P (at most 2 girls) = P (exactly 0 girl, 1 girl or 2 girls)
⇒ P (at most 2 girls) = P (X = 4, X = 3 or X = 2)
⇒ P (at most 2 girls) = 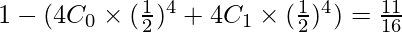
Thus, No. of families having at most 2 girls = 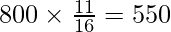
(iv) P(children of both sexes)
⇒ P (children of both sexes) = 1 – P (children of same sex)
⇒ P (children of both sexes) = 1 – {P (all are boys) + P (all are girls)}
⇒ P (children of both sexes) = 1 – {P (X = 4) + P (X = 0)}
⇒ P (children of both sexes) = 
⇒ P (children of both sexes) = 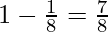
Thus, No. of families having children of both sexes = 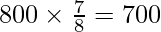
Problem 4: Ten coins are thrown simultaneously. Find the probability of getting at least seven heads?
Solution:
Given: p = Probability of getting a head = 1/2
Thus, q = Probability of not getting a head = 1 – p = 1/2
The probability of getting x heads in a random throw of 10 coins is:
p(x) = 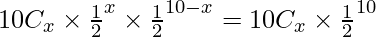 ; x = 0, 1, 2, . . ., 10
; x = 0, 1, 2, . . ., 10
Therefore, probability of getting at least seven heads is given by:
P(X ≥ 7) = P(7) + P(8) + P(9) + P(10)
⇒ P(X ≥ 7) = 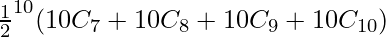
⇒ P(X ≥ 7) = \frac{176}{1024}
FAQs on Bernoulli Trials and Binomial Distribution
Q1: What is a Bernoulli Trial?
Answer:
For a finite number of trials when the probability of success or failure remains the same for all the Trials, then the trial(experiment) is called Bernoulli’s trial.
Q2: What is Binomial Distribution?
Answer:
A binomial distribution is a probability distribution that describes the number of successes in a fixed number of independent trials, where each trial can result in only two possible outcomes, usually referred to as success or failure.
Q3: What are the Characteristics of Binomial Distribution?
Answer:
The characteristics of a binomial distribution include:
- The number of trials, n, is fixed.
- Each trial is independent of the others.
- The probability of success, p, is constant across all trials.
- The outcomes of each trial are mutually exclusive (only one outcome can occur per trial).
- The probability of success, p, and the probability of failure, q (which is equal to 1-p), add up to 1.
Q4: What is the Formula for the Probability of Binomial Distribution?
Answer:
The formula for probability of binomial distribution is giver as follows:
P(X = r) = nCr qn – r pr
Where,
- P(X = r) is the probability of getting exactly k successes,
- n is the number of total trials,
- k is the number of successes in n Trials,
- p is the probability of success,
- q is the probability of failure, and
- p + q = 1 and r = 0, 1, 2, …, n
Q5: What is the Mean of a Binomial Distribution?
Answer:
The mean of the binomial distribution is given by the following formula:
μ = np
Where,
- n is the total number of Trials, and
- p is the probability of success.
Q6: What is the Variance of Binomial Distribution?
Answer:
The variance of a binomial distribution is given as follows:
σ2 = np(1-p)
Where,
- n is the total number of Trials, and
- p is the probability of success.
Q7: What is the Difference between Binomial Distribution and Normal Distribution?
Answer:
The basic difference between the binomial distribution and the normal distribution is that the binomial distribution is discrete, while the normal distribution is continuous.
Share your thoughts in the comments
Please Login to comment...