Definite Integrals of Piecewise Functions
Last Updated :
27 Feb, 2024
Imagine a graph with a function drawn on it, it can be a straight line or a curve or anything as long as it is a function. Now, this is just one function on the graph, can 2 functions simultaneously occur on the graph? Imagine two functions simultaneously occurring on the graph, say, a straight line and a curve, and the limits on the x-axis for which they occur are the same, can this be called a function? No. The two values of the function for a single input is not a Function. Then, how to arrange two functions on a graph? Simple, just make sure that the limits for which they both exist are different and not the same, these types of functions where either on function breaks on different x-axis values or two or more than two functions are defined at different limits are known as piecewise-functions.
Definite Integration
Integration is finding the area between the function and the axis (can be x-axis or y-axis based on the function). Integration can be finite or infinite, for infinite functions, that exist up to infinity or start from infinity, the area for such functions are known as indefinite integrals, whereas if some boundaries are applied to limit the function in some finite value present on the axis, it will be called as definite integrals.
Definite integration has start and end boundaries. Assume the extreme limits go from a to b. The function from a to b shall look like,

Integration is given by ⇢ 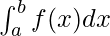
Example: Find the area under the graph of function y=4x, the boundaries are defined from 0 to 5 on x-axis. Solve both by integration and simply solving the area using formula.
Solution:
The function on the graph shall look like,

The above graph shows exactly what area is to be measured,
Integral of y=4x from 0 to 5 = ![Rendered by QuickLaTeX.com \int^5_0{4xdx}\\=4[\frac{x^2}{2}]^5_0\\=2[25-0]\\=50unit^2](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-7cad883afe76e3466cd5c3be35ac3173_l3.png)
The area looks like a triangle and hence, another way of solving this is by simply finding the area of the triangle.
For height of the triangle, at x = 5, y = 4 × 5 = 20 units.
Base = 5 units, Height = 20 units.
Area of the triangle = 1/2 × 5 × 20
= 10 × 5
= 50 units2
Definite Integrals of piecewise functions
In order to integrate functions piecewise, it is required to break the integration at the exact breakpoints. Breaking the integrals will give two different functions for different upper and lower limits, and it becomes easy to integrate them separately. The same can be done for more than two functions, the breakpoints and the number of integration will increase in such case.
Piecewise-function’s can be represented as,
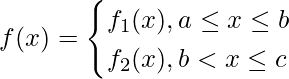

Here, the limit has a break point at c, and the two functions are f1(x) and f2(x).
The above conditional function has definite integrals of fixed end points.
Function with fixed lower endpoints, variable upper endpoints
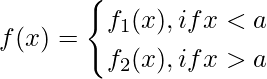
Application of Definite integrals of piecewise function
Below are some examples of piecewise functions that are very often seen in mathematics,
Modulus function are the functions that break at a point, and they are represented as,
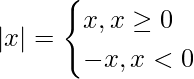
- Greater Integer Function, [x]
In definite integrals, if the value obtained is some decimal, the greater integer condition will bring out the integer part of the value, for example, [8.34] will give 8.
- Fractional Part of Function, {x}
Fractional part of x is derived or obtained from greater integer of the function only.
It is defined as, {x} = x-[x]
Sample Problems
Question 1: A conditional function is given as, 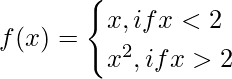
Find the definite integral of 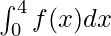
Solution:
The above conditional function has two functions involved, one is a straight line and the other is a parabola, the break point of the limit is 2 and below 2, the function is a straight line x, above 2 or after 2, it is a parabola x2.
Keeping this in mind the definite integral can be easily broken as,
![Rendered by QuickLaTeX.com \int_0^4f(x)dx= \int_0^2xdx + \int_2^4x^2dx \\=[\frac{x^2}{2}]_0^2+[\frac{x^3}{3}]_2^4 \\=2+21.333-2.666\\=20.667](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-acd27c98c3967c2309fb3ca64f7e010d_l3.png)
Question 2: Evaluate the definite integral  , where
, where 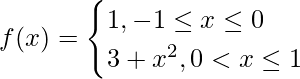
Solution:
The above function has two different functions involved on different limits, the breakpoint of the limit is 0, and before to -1, the function is 1, and after 0 to 1, the function is 3+x2.
Let’s solve,
![Rendered by QuickLaTeX.com \int_{-1}^1f(x)dx= \int_{-1}^01dx + \int_0^13+x^2dx\\=[x]_{-1}^0+[3x]_0^1+[\frac{x^3}{3}]_0^1\\=1+[3-0]+[1/3-0]\\=1+3+1/3\\=4+1/3\\=\frac{13}{3}](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-74635e65bf8472fbe71f40e647fef95b_l3.png)
Question 3: Find the area of the function given below with the help of definite integration,

Solution:
There are three different functions from -1 to 4, y=3, y=2+x, y=4. Let’s integrate these function with the help of piecewise integration of functions.
![Rendered by QuickLaTeX.com \int_{-1}^4f(x)dx= \int_{-1}^13dx + \int_1^22+xdx + \int_2^44dx\\=[3x]_{-1}^1+[2x]_1^2+[\frac{x^2}{2}]_1^2+[4x]_2^4\\=6+3+2-0.5+16-8\\=19-0.5\\=18.5](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-82fc5fd9e568cfddf41ba0290f225d8d_l3.png)
Question 4: Solve the integration  when the function is given as, f(x)= |x|.
when the function is given as, f(x)= |x|.
Solution:
The integration for modulus of x or |x| can be solved only after knowing the meaning of |x|, |x| is defined as,
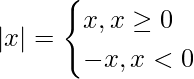
Hence, the function can be broken as,
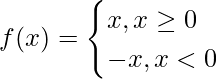
![Rendered by QuickLaTeX.com \int_{-1}^1f(x)dx= \int_{-1}^0-xdx+\int_{0}^1xdx\\=-[\frac{x^2}{2}]_{-1}^0+[\frac{x^2}{2}]_0^1\\=-[0-1/2]+[1/2]\\=1/2+1/2 \\=1](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-c4392ac0171908f5dcd22cff7cad0d6d_l3.png)
Question 5: Evaluate the given function, 
Solution:
The above function is a modulus function and hence, it will have break point, lets find out the break point for |2-x|,
As it is known that the modulus function will have 2 values, one positive and one negative, but it is important to find out where the values or the function as a whole starts to change,
The lower limit is 0, if 0 is put, the value obtained is 2 which is positive, now put 1, value obtained is 1, but if any value above 2 is put, the value if negative, hence, the break point is 2.
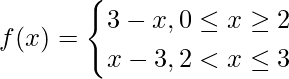
![Rendered by QuickLaTeX.com \int_0^3|3-x|dx= \int_0^2(3-x)dx+\int_2^3(x-3)dx\\=[3x]_0^2-[\frac{x^2}{2}]_0^2+[\frac{x^2}{2}]_2^3-[3x]_2^3\\=6-2+9/2-2+9-6\\=9.5](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-edc613ccafda5977364a57a6ad069361_l3.png)
Like Article
Suggest improvement
Share your thoughts in the comments
Please Login to comment...