As the complexity of the functions increase, we see more and more complex behavior from their graphs, and it becomes harder to graph. There have lots of peaks and valleys in their graphs. It becomes essential to find out the position of these valleys and peaks, the peaks are called maxima and the valleys are called minima. There can be more than one maximum and minima in every graph. These peaks and valleys allow us to find the minimum and the maximum value of the function in an interval. We use derivatives to find the position of these critical points.
Maximum and Minimum Points
Let’s say we have a function f(x), the graph of this function is given below. The maxima and the minima of this function are peaks and troughs present in the graph of this function. For example, we can see in the figure that at x = b and x = a, it is a trough thus it is a minimum, similarly x = a is a maximum. There can be more than one maxima and minima. The minimum value of the function is called global minima and similarly, the maximum value of the function is called global maxima. All other maximas and minimas are called local maxima and local minima.

Let’s see the formal definitions for maxima and minima.
Let’ say f is a function defined in the interval I, Then,
- f is said to have a maximum value in I, if there exists a point c in I such that f(c) > f(x), for all x∈ I.
- f is said to have a minimum value in I, if there exists a point c in I such that f(c) < f(x), for all x∈ I.
- f is said to have an extreme value in I if there exists a point c in I such that f (c) is either a maximum value or a minimum value of f in I.
Example: Find the minimum and maximum value of the function f(x), from the graph given below, f(x) = |x|.

Solution:
In the graph for the given function f(x),
At x = 0, f(x) = 0 and for all x∈ R except x = 0, f(x) > 0.
Thus, minimum value of the function is x = 0.
Maximum value of the function is infinite.
Note:
A function that is monotonically increasing or decreasing has its minima and maxima at the ends of the corresponding interval. For example, the line in the figure below is increasing monotonically. The maxima and minima of the interval are at the ends of the interval.

The functions which have more than one minima and maxima have some local minima and local maxima and global maxima and minima. The figure below has more than one minima and maxima. We call them local minimum and local maximum.

For a real-valued function f and an interior point c in the domain of f. Then,
1. c is called a point of local maxima if there is a h > 0, such that,
f(c) > f(x) for all x in (c – h, c + h)
The value at point c, f(c) is called local maximum.
2. c is called a point of local minima if there is a h > 0, such that,
f(c) < f(x) for all x in (c – h, c + h)
The value at point c, f(c) is called local minimum.
First Derivative Test
Now let us see how to determine the points of minima and maxima. The figure below shows both minima and maxima of two functions. Notice that at the point of local minima and maxima, the slope of the tangent is zero.

The following rule helps us in finding out the difference between maxima and minima in the function below.
For a function f defined in the open interval I, let c be a critical point c in I. Then,
1. Point c is called local maxima. If f'(x) changes sign from positive to negative as x increases through c, i.e, if f'(x) > 0 at every point close to and left of c, and f'(x) < 0 at every point close to and right of c and f'(x) < 0 at every point close to and to the right of c.
2. Point c is called local minima. If f ′(x) changes sign from negative to positive as x increases through c, i.e., if f ′(x) < 0 at every point close to and to the left of c, and f ′(x) > 0 at every point close to and to the right of c.
3. The point is a point of inflection if f ′(x) does not change sign as x increases through c, then c is neither a point of local maxima nor a point of local minima.
This test is called first derivative test.
Second Derivative Test
This test is also used to check for the local minima or maxima at critical points. This is often easier to apply than the first derivative test.
For a function f defined in the open interval I, let c be a critical point c in I. Assuming the function f is twice differentiable at point c,
1. x = c is local maxima if f'(x) = 0 and f”(x) < 0.
2. x = c is local minima, if f'(x) = 0 and f”(x) > 0.
3. This test fails if f'(c) = 0 and f”(c) = 0.
For the third case, we go back to the first derivative test and check.
Let’s see some problems on these concepts.
Sample Problems
Question 1: Find out the critical points for the following function f(x) = x4 – x2.
Solution:
For the function f(x) = x4 – x2. We know that critical points are the points where f'(x) =0
f'(x) = 4x3 – 2x
⇒ f'(x) = 0
⇒ 4x3 – 2x= 0
⇒ x(4x2 – 2) = 0
The roots of this equation are,
x = 0, x = 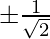
Thus, the critical points are, x = 0, 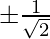
Question 2: Find out the critical points for the following function f(x) =x3 + 3x2 + 3x.
Solution:
For the function f(x) = x3 + 3x2 + 3. We know that critical points are the points where f'(x) =0
f'(x) = 3x2 + 6x + 3
⇒ f'(x) = 0
⇒ 3x2 + 6x + 3= 0
⇒ 3(x2 + 2x + 1) = 0
⇒ 3(x + 1)2 = 0
The roots of this equation are,
x = -1
Thus, the critical points are, x = -1.
Question 3: Find out the relative maxima and minima for the following function,
f(x) = x3 – 3x2 + 3
Solution:
We need to first find the critical points,
f'(x) = 3x2 – 6x
⇒ f'(x) = 0
⇒ 3x2 – 6x= 0
⇒ 3x(x – 2) = 0
⇒ 3x(x – 2) = 0
The roots of this equation are,
x = 0 and x = 2.
Thus, the critical points are, x = 0 and 2.
Now we need to check whether these are maxima or minima. We can use the second derivative test.
f”(x) =6x – 6
At x = 0, f”(x) < 0. Thus, x = 0 is a local maxima.
At x = 2, f”(x) > 0. Thus, x = 2 is a local minima.
Question 4: Find out the relative maxima and minima for the following function in the interval [0,4],
f(x) = 3x + 3
Solution:
We need to first find the critical points,
f'(x) = 3
⇒ f'(x) = 3
Notice that this function has a constant derivative which is positive. That means that this function is constantly increasing in nature. This is a monotonically increasing function.
From the property mentioned above, the monotonically increasing functions have their maxima and minima at the boundary of the interval. Thus, in the interval [0,4], f(x) is monotonically increasing. So, it’s minima lies at x = 0 and maxima at x = 4.
Question 5: Find out the critical points for the following function f(x) =sinx.
Solution:
For the function f(x) = sin(x). We know that critical points are the points where f'(x) =0
f'(x) = cos(x)
⇒ f'(x) = 0
⇒ cos(x)= 0
The roots of this equation are,
x = 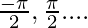
Thus, the critical points are, x = 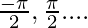
Like Article
Suggest improvement
Share your thoughts in the comments
Please Login to comment...