Definite Integral is nothing but an indefinite integral defined inside a fixed limit. i.e. if we integrate any function within a fixed interval it is called a Definite Integral. The starting point of the interval is the lower limit of the definite integral whereas the endpoint of the interval is the upper limit of the definite integral.
Definite integral is widely used in advanced mathematics or mechanics or others. It is used for calculating the area of irregular curves, and the volume of random shapes. and other.
In this article, we will learn about, Definite Integrals, formulas, applications, and others in detail.
Definition of Definite Integral
The general definition of Definite Integral is that it is the area of the curve under the limit of the definite integral. The definite integral is denoted by  . Here, ‘a’ and ‘b’ are the limits of the integral. “a” is called the upper limit of the integral, and “b” is called the lower limit.
. Here, ‘a’ and ‘b’ are the limits of the integral. “a” is called the upper limit of the integral, and “b” is called the lower limit.
The image given below shows the representation of the Definite Integrals.

Definite Integral
The definite integral can also be defined as the antiderivative of any function in the interval [a, b], and now for any function F(x) whose derivative is, f(x), then in the interval [a, b] its definite integral is defined as,
 = F(b) – F(a)
= F(b) – F(a)
Definite integral formulas are used to evaluate a definite integral. We have two formulas to evaluate a definite integral as mentioned below. The first formula is called the “definite integral as a limit sum” and the second formula is called the “fundamental theorem of calculus”.
 = F(b) – F(a)
= F(b) – F(a)
 = limn–>∞
= limn–>∞  hf(a+rh)
hf(a+rh)
where,
h = (b-a) / n
Evaluating Definite Integrals
Finding the area enclosed by a graph of any function within the limits mentioned (say, [a, b]) on the graph is known as evaluating a Definite Integral. In Definite Integrals, the limit goes from a to b.
![Rendered by QuickLaTeX.com \int_{a}^{b}f(x)=F[a]-F[b]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-3dd04f5be4e16e061dcd20c6df3ba21c_l3.png)
Example: Integrate the definite integral, 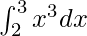
Solution:
Integrating, ![Rendered by QuickLaTeX.com \int_{2}^{3}x^3dx\\ =[\frac{x^4}{4}]_{2}^{3}\\ =20.25-4\\ =16.25](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-2b7960becae5dfdd257f15840ce5038c_l3.png)
Definite Integral as Limit of a Sum
Assuming that ƒ is a continuous function and positive on the interval [a, b]. So, its graph is above the x-axis.
Definite integral  is the area bounded by the curve y = f(x), the ordinates x = a and x = b and x-axis.
is the area bounded by the curve y = f(x), the ordinates x = a and x = b and x-axis.
Now to evaluate this area, consider the region ABCD in the figure below,
.png)
Let x0 = a and xn = b.
Now divide the interval [a, b] into n equal subintervals denoted by [x0, x1], [x1, x2], [x2, x3] ….[xr-1, xr] …..[xn-1, xn]
where x0 = a, x1 = a + h, x2 = a + 2h …. and xn = a + nh or n = . As n ⇢ ∞, h ⇢ 0.
. As n ⇢ ∞, h ⇢ 0.
The region ABCD under consideration is the sum of n subregions, where each subregion is defined on subintervals [xr – 1, xr], where, r = 1, 2, 3, …, n.
It can be seen in the above figure that, now the area of the triangle POFR is calculated as,
A = PQ × PR
⇒ A = (xr– xr–1) × f(xr-1)
As xr– xr–1 → 0, i.e., h → 0, the area above becomes a nearly perfect rectangle. Now the area under the curve can be broken into n different rectangles adding all these rectangles’ areas we get the area under the curve.
![Rendered by QuickLaTeX.com s_{n} = h[f(x_{0}) + .... + f(x_{n})] \\= h\sum^{n-1}_{r=0}f(x_{r}) \\ S_{n} = h[f(x_{1}) + .... + f(x_{n})] \\= h\sum^{n}_{r=1}f(x_{r})](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-74710e935a51e43deea8aab4eb4ddce3_l3.png)
sn and Sn denote the sum of areas of all lower rectangles and upper rectangles raised over subintervals [xr-1, xr] for r = 1, 2, 3,…. respectively.
As n → ∞ strips become narrower and narrower, so, the limiting values of (2) and (3) are the same in both cases and the common limiting value is the required area under the curve.
So,

Now, this equation can also be re-written as,
![Rendered by QuickLaTeX.com \int^{b}_{a}f(x) = \lim_{h \to 0}[f(x) + f(a + h) + f(a + 2h) + f(a + 3h) ......f(a + (n-1)h)] \\](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-8617fe12d663354b20c77ead6cdaae0e_l3.png)
where, 
This expression is knows as definition of definite integral as limit of sum.
Example: Find  as the limit of sum.
as the limit of sum.
Solution:
By the definition given above,
![Rendered by QuickLaTeX.com \int^{b}_{a}f(x) = \lim_{h \to 0}[f(x) + f(a + h) + f(a + 2h) + f(a + 3h) ......f(a + (n-1)h)]](https://quicklatex.com/cache3/5f/ql_6ca66d02d350bfed7f6363f96eb20f5f_l3.png)
Where 
Here, a = 0 and b =2, f(x) = x2 + 1, h = 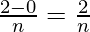
![Rendered by QuickLaTeX.com \int^{2}_{0}(x^{2} + 1) = 2\lim_{n \to \infty}\frac{1}{n}[f(0) + f(\frac{2}{n}) + f(\frac{4}{n}) + ......f(\frac{2(n-1)}{n})] \\ = 2\lim_{n \to \infty}\frac{1}{n}[1 + (\frac{2}{n}^{2} + 1) + \frac{4}{n}^{2} + 1 + ......\frac{2(n-1)}{n}^{2} + 1] \\ = 2\lim_{n \to \infty}\frac{1}{n}[\underbrace{(1 + 1+ .... 1)}_\text{n terms} + \frac{1}{n^{2}}(2^{2} + 4^{2} + ..... (2n - 2)^{2}] \\ = 2\lim_{n \to \infty}\frac{1}{n}[n + \frac{4}{n^{2}}(1^{2} + 2^{2} + .... (n-1)^{2}] \\ = 2\lim_{n \to \infty}\frac{1}{n}[n + \frac{4}{n^{2}}\frac{((n-1)n(2n-1)}{6}] \\ \text{Evaluating above limit} = \frac{14}{3}](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-4023d5ac494528232a81ebd50883e610_l3.png)
Definite Integral and Fundamental Theorems of Calculus
We have defined definite integral as the area enclosed by function f(x) from x = a to x = b. So, the definite integral is also called the area function. We denote this area function by A(x), it is given by,
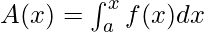
Based on this definition, we will state two fundamental theorems.
First Fundamental Theorem of Calculus
Let f be a continuous function on the closed interval [a, b], and let A (x) be the area function. Then A′(x) = f (x), for all x ∈ [a, b].
Second Fundamental Theorem of Calculus
Let f be a continuous function defined on the closed interval [a, b] and F be an antiderivative of f. Then ![Rendered by QuickLaTeX.com \int_{a}^{b}f(x)dx = [F(x)]^{b}_{a} = F(b) - F(a)](https://quicklatex.com/cache3/26/ql_b95dbbbc9076225bc4b0a15897268926_l3.png)
Note: This theorem is really useful as it gives us means of calculating a definite integral without actually calculating it a limit of a sum.
Read More about Fundamental Theorem of Calculus.
Steps for Calculating Definite Integral
Steps for Calculating the definite integral using the Fundamental theorem of calculus are given below,
Step 1: Find the indefinite integral . Let’s call it F(x). There is no need to keep a constant “C”, it will cancel out anyway in the end.
. Let’s call it F(x). There is no need to keep a constant “C”, it will cancel out anyway in the end.
Step 2: Find F(b) – F(a) = ![Rendered by QuickLaTeX.com [F(x)]^a_b](https://quicklatex.com/cache3/e4/ql_722a9001a2a911c47e03c693a2c5c9e4_l3.png) which is the value of this definite integral.
which is the value of this definite integral.
Example: Calculate the integral: 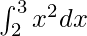
Solution:
Solving Indefinite Integral we get,

Let the value of definite integral be S. and a= 2 and b = 3
S = F(b) – F(a)
S = (3)3/3 – (2)3/3
S = 9 – 8/3
= 19/3
For more details Check, How to Calculate a Definite Integral?
Properties of Definite Integral
Various Properties of Definite Integral are
Property 1: This property states that the limits are interchangeable on definite integrals with an extra negative sign.
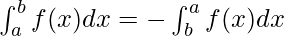
Property 2: This property has limits from a to itself; therefore, the figure is nothing but a point, and there is no area of a point. Therefore, the integration with such limits is always zero.

Property 3: This property is valid since C is a Constant that can be taken out from the integration easily as it is not included in the function given.

Property 4: This property states that the value of the Integration will remain the same after splitting the function connected with sum or difference.
![Rendered by QuickLaTeX.com \int_{a}^{b}[f(x){_{-}^{+}}g(x)]dx= \int_{a}^{b}f(x)dx{_{-}^{+}}\int_{a}^{b}g(x)dx](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-9c991ed946dc9843661594f7d1c606ee_l3.png)
Property 5: This property states that the variable used to integrate the function does not matter as long as the limits and the value of the function are the same.
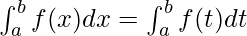
Property 6: ![Rendered by QuickLaTeX.com \int_{a}^{b}cdx=c[b-a]](https://quicklatex.com/cache3/87/ql_a4dd0baaf16a01ffa443b62c67fdac87_l3.png) where, C is any constant.
where, C is any constant.
Property 7: This property says that if the value of the function is greater than zero, then its integration will also be greater than zero. If f(x) ≥ 0 for a ≤ x ≤ b then,
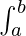 f(x)dx ≥ 0.
f(x)dx ≥ 0.
Property 8: If the value of a function is greater than the value of another function, then the integration of that function will also be greater than the integration of the other function. If f(x) ≥ g(x) for a ≤ x ≤ b then,

Property 9: If p ≤ f(x) ≤ P for a ≤ x ≤ b then p[a-b]≤  ≤ P[a-b]
≤ P[a-b]
Property 10: 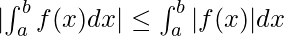
Definite Integral by Parts
Definite Integral can be broken into two parts and then we can solve them easily. The various methods in which we can break Definite integrals are,
Method 1: 
Method 2: We can also break definite integrals using,
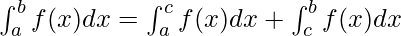
Read More about Integration by Parts.
Applications of Definite Integral
Definite integral finds its application in various fields, some of the important applications of the definite integral are,
- Finding areas of various curves such as circles, parabolas, ellipses, and others.
- Solving the infinite series and finding their sum.
- Finding Divergence and curl of the vectors and others.
Read More,
Definite Integral Examples
Example 1: Find the Integral: 
Solution:
Solving, ![Rendered by QuickLaTeX.com \int_{0}^{\frac{\pi}{6}}cos3xdx=[\frac{sin3x}{3}]_{0}^{\frac{\pi}{6}}\\\frac{1}{3}[sin(\frac{\pi}{2}-sin0)]=\frac{1}{3}[1-0]=\frac{1}{3}](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-1872872b2e9d2aa34b320747f5a4e2b0_l3.png)
Example 2: Evaluate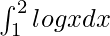
Solution:
![Rendered by QuickLaTeX.com \int_{1}^{2}logx.1dx=[logx.x]_{1}^{2}-\int_{1}^{2}\frac{1}{x}.xdx\\](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-ea8112ce553aa3e5679ce5f0bc53ad96_l3.png)
2log2-2+1=(2log2-1)
Example 3: Integrate 
Solution:

Applying G.P, a=1. r=e2/n, we will get,
![Rendered by QuickLaTeX.com \int_{0}^{2}e^xdx=(2)lim_{n\to\infty}\frac{1}{n}[\frac{e^\frac{2n}{n}-1}{e^\frac{2}{n}-1}]\\2lim_{n\to\infty}\frac{1}{n}[\frac{e^2-1}{e^\frac{2}{n}-1}](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-0398c396025766c13f150778a2cbfafe_l3.png)
Using,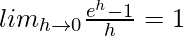
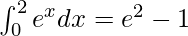
Example 4: Evaluate 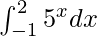
Solution:
a=-1, b=2, f(x)=5x
h=(b-a)/n=3/n, nh=3
By definition: ![Rendered by QuickLaTeX.com \int^{b}_{a}f(x) = \lim_{h \to 0}[f(x) + f(a + h) + f(a + 2h) + f(a + 3h) ......f(a + (n-1)h)] \\](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-8617fe12d663354b20c77ead6cdaae0e_l3.png)
![Rendered by QuickLaTeX.com \int_{-1}^{2}5^xdx=\lim_{h\to0}h[f(-1)+f(-1+h)+f(-2+h)+.....f(-1+(n-1)h)]\\\lim_{h\to0}h[5^{-1}+5^{-1}.5^h+.....5^{-1}.5^{(n-1)h}\\\lim_{h\to0}h[\frac{5^-1.(5^{nh}-1)}{5^h-1}]\\\lim_{h\to0}\frac{h}{5^h-1}5^{-1}(5^3-1)](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-2713bf8b33bfd51828752bd201f0c101_l3.png)
![Rendered by QuickLaTeX.com \frac{1}{log5}[5^2-\frac{1}{5}]=\frac{124}{5log5}](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-4e8cc64684083e3dd579e02468d27ba7_l3.png)
Example 5: Evaluate, 
Solution:
![Rendered by QuickLaTeX.com \int_{0}^{\pi/2}cosx dx= [sinx]_{0}^{\pi/2}\\(sin\pi/2)-(sin0)=1-0=1](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-ee54e4163b25cf19ac0244e99c9cdc0e_l3.png)
Definite Integral – FAQs
What is a definite integral?
A definite integral is an integral which is calculated on a finite interval. It generally denotes the area under the curve. A definite integral is denoted by  , where b is the lower limit of the integral and b is the upper limit of the integral.
, where b is the lower limit of the integral and b is the upper limit of the integral.
What is the formula for definite integral?
For any function f(x) the formula used for calculating the definite integral in the interval [a, b] is,
 = F(b) – F(a)
= F(b) – F(a)
What is a definite integral used for?
Definite integral is used for various purposes but its most important use of definite integral is finding the area of the curve.
How to Evaluate a Definite Integral?
Definite Integral is calculated using the steps given below,
Step 1: Solve for the indefinite integral
Step 2: Substitute the upper and lower limit in the solution of Indefinite Integral.
Step 3: Subtract the Result of the upper limit with the lower limit.
What are definite integral and indefinite integral?
Integrals are also called anti derivatives they can be assumed as the inverse of differentiation. The main difference between Indefinite Integrals and Definite Integrals is Indefinite integrals are evaluated without any limit whereas, definite integrals always have proper limits.
Share your thoughts in the comments
Please Login to comment...