Riemann sums allow us to calculate the area under the curve for any arbitrary function. These formulations help us define the definite integral. The basic idea behind these sums is to divide the area that is supposed to be calculated into small rectangles and calculate the sum of their areas. These areas are not accurate, but they help a lot in getting an idea about the actual area. The more the number of rectangles, the closer it takes us to the actual area. Let’s look at Riemann sums with sigma notations.
Riemann Sums
Definite integrals are an important part of calculus. They are used to calculate the areas, volumes, etc of arbitrary shapes for which formulas are not defined. Analytically they are just indefinite integrals with limits on top of them, but graphically they represent the area under the curve. The limits denote the boundaries between which the area should be calculated. These concepts hold a lot of importance in the field of electrical engineering, robotics, etc. For defining integrals, Riemann sums are used in which we calculate the area under any curve using infinitesimally small rectangles. Let’s look at this interpretation of definite integrals in detail.

Now this area can be divided into a number of rectangles, assuming the area is divided into ‘n’ rectangles of equal width. Some of these rectangles go above the actual value of the function and some go below, which means that the area is overestimated and underestimated in certain parts. The height of these rectangles is determined by the value of the function in the middle of the interval.

In the definite integral notation, this area will be represented as,
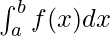
This area can be approximated by dividing the area under the curve into n equally sized rectangles. So, the interval [a, b] is divided into n-subintervals defined by the points.
a = x0 < x1 < x2 < …. xn-2< xn-1 < xn = b
Then, the n intervals are,
[x0, x1], [x1, x2], …. [xn-1, xn]
So, for the ith rectangle, the width will be, [xi-1, xi].
The area for ith rectangle Ai = f(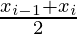 )(xi — xi-1)
)(xi — xi-1)
So, the total area will be 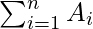
This sum is called Riemann sum.
Riemann Sums in Sigma Notation
Assume that the goal is to calculate the area under the graph of the function f(x) = x2, the area will be calculated between the limits x = 0.5 to x = 4.5.

Divide the interval into four equal parts, the intervals will be [0.5, 1.5], [1.5, 2.5], [2.5, 3.5] and [3.5, 4.5].
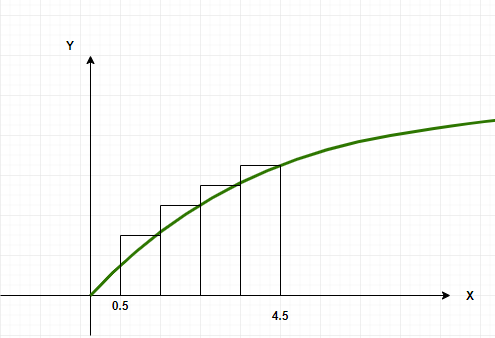
The riemann sum then, can be written as follows,
A(1) + A(2) + A(3) + A(4) = 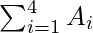
Let the heights of the interval be the values of the function at the end of the rectangle. This is called the right sum Riemann sum. Let xi denote the right endpoint of the ith rectangle.
So, the formula for xi = 0.5 + i. Now, the value of the function at these points becomes,
f(xi) = (0.5 + i)2
So, A(i) = (height)(width)
= (0.5 + i)2
The Riemann sum becomes,
A(1) + A(2) + A(3) + A(4) = 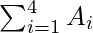
⇒ A(1) + A(2) + A(3) + A(4) = 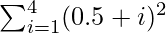
So, this way almost all the riemann sums can be represented in a sigma notation.
To summarize the whole process,
Step 1: Find out the width of each interval. Let’s denote the width of interval with 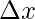
Step 2: Let xi denote the right-endpoint of the rectangle xi = a +  x.i
x.i
Step 3: Define the area of each rectangle.
Step 4: Sum the areas
Sample Problems
Question 1: Consider a function f(x), its area is calculated from riemann sum from x = 4 to x = 10, the whole area is divided into 5 rectangles. Find the interval width.
Solution:
The whole length is divided into 5 equal parts,
xi = 4 and xl = 10,
Width of an interval is given by = 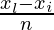
Where xi – initial point, and xl – last point and n= number of parts
n = 5
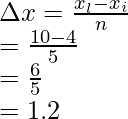
Question 2: Consider a function f(x) = x, its area is calculated from riemann sum from x = 0 to x = 5, the whole area is divided into 5 rectangles. Find the riemann sum in sigma notation
Solution:
Step (i): Calculate the width
The whole length is divided into 5 equal parts,
xi = 0 and xl = 5,
Width of an interval is given by = 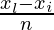
Where xi = initial point, and xl – last point and n= number of parts
n = 5
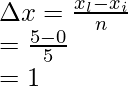
Step(ii):
a = 0,
xi = 0 + 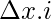
⇒ xi = i
Step (iii)
Ai = Height x Width
= f(xi) 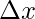
= (i)
Total Area = A(1) + A(2) + A(3) + A(4) + A(5)
= 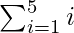
Question 3: Consider a function f(x) = 5 – x, its area is calculated from riemann sum from x = 0 to x = 5, the whole area is divided into 5 rectangles. Find the riemann sum in sigma notation
Solution:
Step (i): Calculate the width
The whole length is divided into 5 equal parts,
xi = 0 and xl = 5,
Width of an interval is given by = 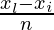
Where xi = initial point, and xl – last point and n= number of parts
n = 5
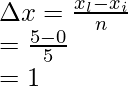
Step(ii):
a = 0,
xi = 0 + 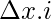
⇒ xi = i
Step (iii)
Ai = Height x Width
= f(xi) 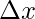
= (5 – i)(1)
= 5 – i
Total Area = A(1) + A(2) + A(3) + A(4) + A(5)
= 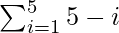
Question 4: Consider a function f(x) = √x, its area is calculated from riemann sum from x = 0 to x = 4, the whole area is divided into 4 rectangles. Find the riemann sum in sigma notation
Solution:
Step (i): Calculate the width
The whole length is divided into 4 equal parts,
xi = 0 and xl = 4,
Width of an interval is given by = 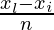
Where xi = initial point, and xl – last point and n= number of parts
n = 4
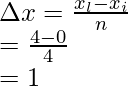
Step(ii):
a = 0,
xi = 0 + 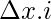
⇒ xi = i
Step (iii)
Ai = Height × Width
= f(xi) 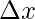
= (√i)(1)
= √i
Total Area = A(1) + A(2) + A(3) + A(4)
= 
Question 5: Consider a function f(x) = ex + 1, its area is calculated from riemann sum from x = 0 to x = 4, the whole area is divided into 4 rectangles. Find the riemann sum in sigma notation
Solution:
Step (i): Calculate the width
The whole length is divided into 4 equal parts,
xi = 0 and xl = 4,
Width of an interval is given by = 
Where xi = initial point, and xl – last point and n= number of parts
n = 4
Step(ii):
a = 0,
xi = 0 + 
⇒ xi = i
Step (iii)
Ai = Height x Width
= f(xi) 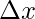
= (ei + 1)(1)
= ei + 1
Total Area = A(1) + A(2) + A(3) + A(4)
= 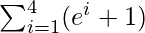
Question 6: Consider a function f(x) = x2 + x, its area is calculated from riemann sum from x = 0 to x = 6, the whole area is divided into 3 rectangles. Find the riemann sum in sigma notation
Solution:
Step (i): Calculate the width
The whole length is divided into 4 equal parts,
xi = 0 and xl = 6,
Width of an interval is given by = 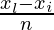
Where xi = initial point, and xl – last point and n= number of parts
n = 3
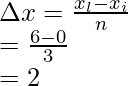
Step(ii):
a = 0,
xi = 0 + 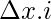
⇒ xi = 2i
Step (iii)
Ai = Height x Width
= f(xi) 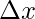
= (i2 + i)(2)
Total Area = A(1) + A(2) + A(3) + A(4) + A(5) + A(6)
= 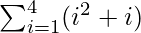
Like Article
Suggest improvement
Share your thoughts in the comments
Please Login to comment...