Inverse of a Matrix by Elementary Operations – Matrices | Class 12 Maths
Last Updated :
17 Nov, 2020
The Gaussian Elimination method is also known as the row reduction method and it is an algorithm that is used to solve a system of linear equations. It is usually understood as a sequence of operations performed on the corresponding matrix of coefficients. This algorithm is used to find :
- The rank of a matrix.
- The determinant of a matrix.
- The inverse of a matrix.
The operations we can perform on the matrix to modify are:
- Interchanging/swapping two rows.
- Multiplying or Dividing a row by a positive integer.
- Adding or subtracting a multiple of one row to another.
Now using these operations we can modify a matrix and find its inverse. The steps involved are:
- Step 1: Create an identity matrix of n x n.
- Step 2: Perform row or column operations on the original matrix(A) to make it equivalent to the identity matrix.
- Step 3: Perform similar operations on the identity matrix too.
Now the resultant identity matrix after all the operations is the inverse matrix.
Examples
Note:
Here, R1: Row 1, R2: Row 2, R3: Row 3
Example 1: Find the inverse of the following matrix by elementary operations?

Solution:
Let’s perform row or column operations on the original matrix(A) to make it equivalent to the identity matrix.
Step 1: Interchange R2 and R3 rows (to make A[2][2] = 1)
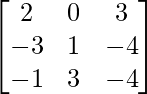
Step 2: R1 = R1 + R3 (to make A[1][1] = 1)
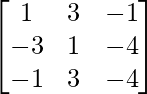
Step 3: R2 = R2 – 3R3 (to make A[2][1] = 0)
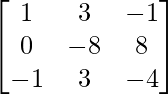
Step 4: R3 = R3 + R1 (to make A[3][1] = 0)
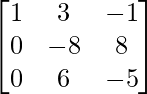
Step 5: R2 = R2/-8 (to make A[2][2] = 1)
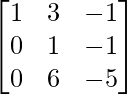
Step 6: R1 = R1 – R2 (to make A[1][3] = 0)
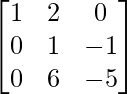
Step 7: R3 – 6R2 (to make A[3][2] = 0)
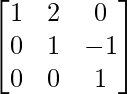
Step 8: R2 = R2 + R3 (to make A[2][3] = 0)

Step 9: R1 = R1 – 2R2 (to make A[1][2] = 0)
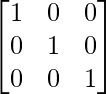
Now perform the same operation as above on the identity matrix. Result after each similar operations as above on the identity matrix, we get:
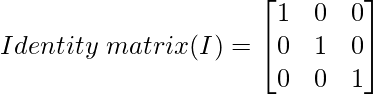
Step 1: Interchange R2 and R3 rows
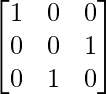
Step 2: R1 = R1 + R3

Step 3: R2 = R2 – 3R3
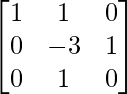
Step 4: R3 = R3 + R1
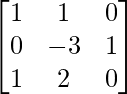
Step 5: R2 = R2/-8
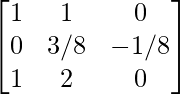
Step 6: R1 = R1 – R2
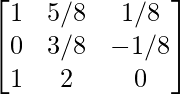
Step 7: R3 – 6R2
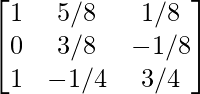
Step 8: R2 = R2 + R3
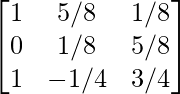
Step 9: R1 = R1 – 2R2
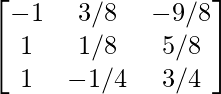
So, the inverse of matrix A is:
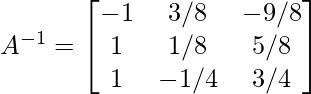
Example 2: Find the inverse of the following matrix by elementary operations?
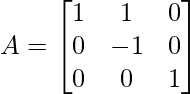
Solution:
Step 1: R1 = R1 + R2
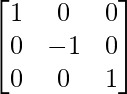
Step 2: R2 = R2 x -1
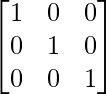
Similar operations on the identity matrix will result in:
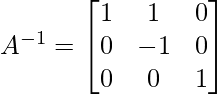
Example 3: Find the inverse of the following matrix by elementary operations?
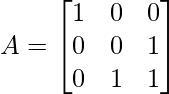
Solution:
Step 1: Swap R2 and R3
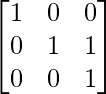
Step 2: R2 = R2 – R3
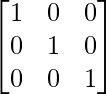
Similar operations on the identity matrix will result in:
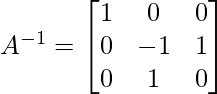
Like Article
Suggest improvement
Share your thoughts in the comments
Please Login to comment...