Derivatives as Rate of Change
Last Updated :
16 May, 2021
Derivatives are considered a mathematical way of analyzing the change in any quantity. We have studied calculating the derivatives for different kinds of functions such as trigonometric functions, exponential functions, polynomials, and implicit functions. Derivatives can be calculated through two methods mainly: Limit Based methods or using different formulas and rules such as product rules, quotient rule, or a chain rule. Derivatives have different applications which makes them very useful in dealing with physical phenomena in the real world. Let’s see some of these applications.
Rate of Change
Derivatives are the basic fundaments that are used in differential calculus. They are used to show the characteristics of the Function, whether they are increasing, decreasing, etc. Imagine we have two quantities that vary with one another. Let’s say these quantities are denoted by “x” and “y”. They are related to each other by some rule
y = f(x)
Then the derivative of this function, that is  is the rate of change of y with respect to x, which tells how y changes with respect to x.
is the rate of change of y with respect to x, which tells how y changes with respect to x.
Example: Find the rate of change of volume of a cube whose sides are increasing at the rate of 2 m/s.
Solution:
Let’s say the length of the side of cube is “a”. The volume of cube is given by, V = a3.
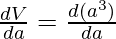
⇒ 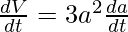
⇒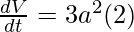
⇒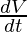 = 6a2 m3/s.
= 6a2 m3/s.
Increasing and Decreasing Functions
Derivatives are also used in finding out whether the function is increasing or decreasing or none of them. The figure given below shows the function f(x) = x2.
Notice in the figure, the function is decreasing in the interval (-∞, 0) and increasing in the interval (0,∞).
In an interval I contained in the domain of real valued function “f”. Then, f is said to be,
- Increasing on I, if x1 < x2 in I ⇒ f(x1) ≤ f(x2) for all x1, x2 ∈ I.
- Strictly Increasing on I, if x1 < x2 in I ⇒ f(x1) < f(x2) for all x1, x2 ∈ I.

- Decreasing on I, if x1 < x2 in I ⇒ f(x1) ≥ f(x2) for all x1, x2 ∈ I.
- Strictly Decreasing on I, if x1 < x2 in I ⇒ f(x1) > f(x2) for all x1, x2 ∈ I.


Now we know the definitions for increasing and decreasing functions. Let’s see how to recognize a function that is increasing or decreasing in an interval.
Let’s say f is continuous on [a, b] and differentiable on the open interval (a, b). Then,
- f is increasing in (a, b) if f'(x) > 0 in the interval [a, b].
- f is decreasing in (a, b) if f'(x) < 0 in the given interval.
- f is constant if f'(x) = 0.

Sample Problems
Question 1: Let’s say we have a circle whose radius is increasing. Find the rate of change of area with radius when r = 4cm.
Solution:
Let’s say “A” is the area of the circle and “r” be the radius of the circle.
A = πr2
Differentiating it with respect to radius.
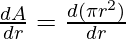
⇒ 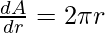
At r = 4.
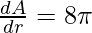
Question 2: Let’s say we have a rectangle whose sides are changing every second. The length is increasing at the rate of 3 m/s while the breadth is increasing at 8 m/s. Calculate the rate at which the area of the rectangle is increasing when length = 8m and breadth = 5m.
Solution:
Let, x be the length of the rectangle and y be the breadth of rectangle.
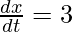 And
And 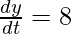
The area of rectangle is given by,
A = xy
Differentiating the equation w.r.t time.
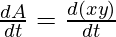
⇒ 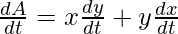
⇒ 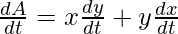
⇒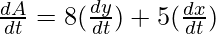
⇒ 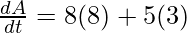
⇒ 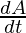 = 64 + 15
= 64 + 15
Question 3: For the given curve, find the points where the value of the rate of change of y is zero.
y = x2 + x
Solution:
y = x2 + x
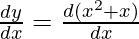
⇒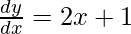
This rate of change must be zero,
2x + 1 = 0
⇒ x = 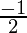
Thus, at x = 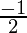 the rate of change is zero.
the rate of change is zero.
Question 4: Prove that the function discussed above, f(x) = x2 is increasing in the interval (0, ∞).
Solution:
According to above definition, a function in increasing in any interval if its derivative is greater than zero in that interval.
f(x) = x2
Differentiating with respect to x,
f'(x) = 2x
For the given interval (0,∞) f'(x) > 0.
Thus, the function is increasing in the given interval.
Question 5: Find the intervals where the function f(x) = x2 + 5x + 6 is increasing or decreasing.
Solution:
Given f(x) = x2 + 5x + 6
f'(x) = 2x + 5
We need to study the sign of the derivative to find the intervals where this function is increasing or decreasing.
f'(x) < 0
⇒ 2x + 5 < 0
⇒ x < 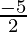
f'(x) > 0
⇒ 2x + 5 > 0
⇒ x > 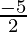
Thus, the function is increasing in (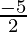 , ∞) and is decreasing in (-∞,
, ∞) and is decreasing in (-∞, 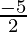 ).
).
Share your thoughts in the comments
Please Login to comment...