Separable Differential Equations

Separable differential equations are the differential equation in which we can easily separate the variables of the differential equation and then the solution of the differential equation is done by individually solving them. The basic form of the Separable differential equations is dy/dx = f(x) g(y), where x is the independent variable and y is the dependent variable. The solution of the above differential equation is done by separating both the variables on either side of the equal sign as,

dy/g(y)  = dx/f(x)

and then integrating them individually.

This method of solving separable differential equations was first proposed by G. Leibniz in 1691 and was finalized by J. Bernoulli in 1694. In this article, we will learn about the separable differential equation, its solution, and others in detail.

What are Separable Differential Equations?

All the differential equations in which we can separate the variable from each other are called the separable differential equation the general form of the separable differential equation is dy/dx = f(x) g(y). We can easily solve these types of equations by simply separating the variables in the differential equation and then integrating them individually.

All the ways in which we can write the separable differential equation are,

• dy/dx = f(x) g(y)
• dy/ g(y) = dx f(x)
• dy/dx = f(x)/g(y)
• g(y) dy = f(x) dx

Variable Separable Differential Equations Definition

We define the variable separable differential equation as the equation of the form dy/dx = f(x) g(y), where f(x) and g(x) are the functions of the x and y. The solution to these equations is achieved by separating the variables and then integrating them separately.

The image shown below shows the basic method of separating  

Examples of Separable Differential Equations

Various examples of separable differential equations are,

• dy/dx = (2x³ + 6)(y² – 7)
• dy/dx = sec x cosec y
• dy/dx = e^ye^x
• dy/dx = sin y cos x

Identifying Separable Equations

The first-order differential equation is a separable differential equation if and only if it can be written as

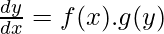
Where,

• f(x) is a function of x that does not contain y.
• g(y) is a function of y that does not contain x.

If it is not possible, to write the equation in this form we call the equation not a separable differential equation.

Note: In order to solve this type of differential equation we have to separate all y’s on one side and x’s on another side of the equal sign.

Solving Separable Differential Equations

Separable differential equations can be easily solved using the steps discussed below,

Step 1: Arrange the given differential equation, in the form, dy/dx = f(x) g(y).

Step 2: Separate the dependent and the independent variable on either side of the equal sign. As, dy/g(y) = d(x)f(x).

Step 3: Integrating both sides individually to get the required solution ∫dy/g(y) = ∫ f(x) dx.

This can be understood with the example discussed below,

Example: Solve dy/dx = x³/y².

Solution:

Given DE, dy/dx = x³/y²

⇒ dy(y²) = x³(dx)

Integrating both sides

∫dy(y²) = ∫x³(dx)

⇒ y²⁺¹/(2+1) = x³⁺¹/(3+1) + c

⇒ y³/3 = x⁴/4 + c

This is the solution to the given differential equation.

Initial Value Problem Separable Differential Equations

We know how to solve the differential equation given in the separable form and this can also be achieved if the initial condition is given. In the differential equation if the initial condition is given we can easily find the value of the integration constant and this helps us to find the exact solution to the differential equation. The example discussed below is the initial value problem for separable differential equations.

Example: Solve dy/dx = (x³ + 2)/(y² – 2) and when y(0) = 0.

Solution:

Given DE,  dy/dx = (x³ + 2)/(y² – 2)

⇒ dy(y² – 2) = (x³ + 2)(dx)

Integrating both sides

∫dy(y² – 2) = ∫x³(x³ + 2)

⇒ y²⁺¹/(2+1) -2y = x³⁺¹/(3+1) + 2x + c

⇒ y³/3 – 2y = x⁴/4 + 2x + c…(i)

Using the initila condition y(0) = 0

x = 0 and then y = 0

⇒ 0 – 0 = 0 + 0 + c

⇒ c = 0

Thus from eq (i)

y³/3 – 2y = x⁴/4 + 2x + c

⇒ y³/3 – 2y = x⁴/4 + 2x

This is the solution to the given differential equation.

Read More,

• How to solve Differential Equations?
• Exact Differential Equations
• Partial Differential Equations

Solved Examples on Separable Differential Equations

Example 1: Find whether the differential equation dy/dx = f(x) + g(y) is variable separable or not.

Solution:

Given DE,

dy/dx = f(x) + g(y)

We know that in the above equation we can not seperate the variables.

dy/dx = f(x) + g(y)

Thus, the given equation is not variable seperable.

Example 2: Find the solution of the differential equation dy/dx = (x+1)/(2-y), (y≠2). 

Solution:

Given DE,

dy/dx = (x+1)/(2-y)

⇒ (2-y) dy = (x+1) dx

Integrating both side

∫(2-y) dy = ∫(x+1) dx 

⇒ ∫2 dy- ∫y dy = ∫x dx + ∫1 dx

⇒ 2y − (y²/2) = (x²/2) + x + C

⇒ 2y − (y²/2) − (x²/2) − x − C = 0

This is the general solution of the given differential equation.

Example 3: Find the general solution of the differential equation dy/dx = (1+y²)/(1+x²).

Solution:

Given DE, dy/dx = (1+y²)/(1+x²)

⇒ dy/(1+y²) = dx/(1+x²)

Inytegrating both side

∫dy/(1+y²) = ∫dx/(1+x²)

⇒ tan^-1y = tan^-1x + C

⇒ tan^-1x – tan^-1y + C = 0

This is the general solution of the given differential equation.

Example 4: Find the general solution of the differential equation dy/dx = -4xy².

Solution:

given DE, dy/dx = -4xy²

⇒ dy/y² = -4x dx

Integrating both side

∫dy/y² = ∫-4x dx

⇒ -(1/y) = -4(x²/2) + C

⇒ -(1/y) = -2x+C

⇒ -2x + (1/y) + C =0

This is the general solution of the differential equation.

Example 5: Solve the following differential equation dy/dx=6xy², y(1) = 1/25

Solution:

Given DE, dy/dx = 6xy²

⇒ dy/y²  =  6x dx

Integrating both sides

∫dy/y² = ∫6x dx

⇒ ∫dy/y² = 6∫x dx

⇒ -(1/y) = 6(x²/2) + C

⇒ -(1/y) = 3x² + C…(i)

This is the general solution of the differential equation.

Using the Intial condition,

x = 1 then y = 1/25

⇒ -25 = 3 + C

⇒ C = -28

Substituting the value of C in eq (i)

-(1/y) = 3x²-28

⇒ y(3x²-28) + 1 = 0

Example 6: Solve the following differential equation dy/dx = (3x² + 4x – 4)/(2y – 4), y(1) = 3.

Solution:

Given DE, dy/dx = (3x² + 4x – 4)/(2y – 4)

⇒ (2y-4)dy = (3x²+4x-4)dx

Integrating both side,

∫(2y-4)dy = ∫(3x²+4x-4)dx

⇒ ∫2y dy – ∫4 dy = ∫3x² dx + ∫4x dx – ∫4 dx

⇒ y² – 4y = x³ + 2x² – 4x + C…(i)

Using the intial condition,

x = 1 then y = 3

⇒ 3² – 4×3 = 1³ + 2×1² – 4×1 + C

⇒ C = -2

From eq (i)

y²-4y = x³+2x²-4x-2

Which is the required solution.

FAQs on Separable Differential Equations

Q1: What are Variable Separable Differential Equations in Calculus?

Answer:

Generally, the differential equation of the form dy/dx = f(x)/g(y) is called a variable separable differential equation. In these equations, we can easily separate both variables and the differential variable and can arrange them on either side of the equal sign (=).

Q2: How to Identify Separable Differential Equations?

Answer:

We can easily identify the separable differential equation by separating the independent variable and dependent variable on either side of the equal sign. If we are able to separate the variables then the equation is a separable differential equation.

Q3: How to solve Separable Differential Equations?

Answer:

Separable differential equations are easily solved by arranging all the dependent variables on one side of the equal sign and the independent variable on the opposite side of the equal sign and then integrating both sides separately to get the final answer.

Q4: What is the Difference Between Linear and Separable Differential Equations?

Answer:

The differential equation where the power of the derivative dy/dx is one and they are written in the form,

dy/dx + Py = Q

Where P and Q are the function of x is called the linear differential equation.

Whereas the equation in which we can easily separate the dependent variable and the independent variable along with their differential variable is called the separable differential equation

Q5: What are Non-Separable Differential Equations?

Answer:

All the differential equations where we can not separate the independent variable (x) and the dependent variable (y) are called the non-separable differential equation.

Q6: How to Solve Non-Separable Differential Equations?

Answer:

We can solve the non-separable differential equations by various methods which are,

• Using the Homogenous Differential Equation method.
• Using the Exact Differential Equation method.
• Using the Linear Differential Equation method.