Particular Solutions to Differential Equations
Last Updated :
24 Jun, 2021
Indefinite integrals are the reverse of the differentiation process. Given a function f(x) and it’s derivative f'(x), they help us in calculating the function f(x) from f'(x). These are used almost everywhere in calculus and are thus called the backbone of the field of calculus. Geometrically speaking, the integrals represent the area and volume under the curve. Often the curves are complicated and the formulas for volume and areas are available for only a handful of curves. In those cases, it becomes necessary to learn the generalized way of calculating the areas and the volume for arbitrary shapes.
Indefinite Integrals
In order to calculate the integrals, it is essential to know how to calculate the anti-derivatives of a function. An anti-derivative of the function f(x) is a function whose derivative is equal to f(x). That is if F'(x) = f(x), the F(x) will be called the anti-derivative of the function f(x). Also, it should be kept in mind that anti-derivatives are not unique, a function can have infinitely many anti-derivatives. An integral is denoted by the sign ∫.
F'(x) = f(x),
F(x) = ∫f(x) + C
Where C, is an arbitrary constant.
The symbol ∫ is called an integral symbol, the function f(x) is called the integrated, and x is called the variable of integration.
Properties of Integration
Property 1: ∫kf(x)dx= k∫f(x)dx
Property 2: ∫f(x)± g(x)dx= ∫f(x)dx± ∫g(x)dx
Property 3: ∫(f1(x)dx± f2(x)dx± f3(x)dx….)= ∫f1(x)dx± ∫f2(x)± ∫f3(x)dx…
Integrals of Common Functions
Integrals of common functions can be inferred directly from their derivatives only. It is essential to remember the anti-derivatives for these standard functions. It makes it easier to calculate the integrals, which are usually a combination of some standard functions. For example, for the function F(x), and its derivative f(x). This can be re-written as,
F'(x) = f(x)
F(x) = ∫f(x) + C
For example,
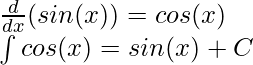
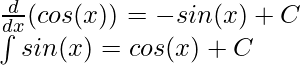
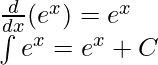
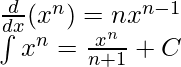
The above rule does not apply when x = -1,
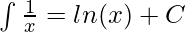
These functions and their integrals can be summarized in the table below:
| Function | Integral |
| xn | 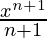 |
| sin(x) | -cos(x) |
| cos(x) | sin(x) |
| ex | ex |
| sec2(x) | tan(x) |
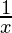 | ln(x) |
Particular Solutions to Differential Equation – Rational Function
Usually, constants are not given that much importance. But in some cases, it becomes important when. For example, consider the given function f'(x) = 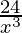 . It is given that f(2) = 12. The goal is to find out f(-1).
. It is given that f(2) = 12. The goal is to find out f(-1).
Let’s re-write the given functions,
f(x) = ∫f'(x) = ∫x-3 = -12x2 + C
It is given that,
f(2) = 12
⇒ -12(2)2 + C = 12
⇒C = 60
Plugging the value of C into the equation of f(x),
f(x) = -12x2 + 60
f(-1) = -12(-1)2 + 60
f(-1) = 48
Particular Solutions to Differential Equation – Exponential Function
The above case was for rational functions. This time, let’s consider the similar case for exponential functions. Consider the function f'(x) = 5ex, It is given that f(7) = 40 + 5e7, The goal is to find the value of f(5). Re-writing the given functions,
f(x) = ∫f'(x) = ∫5ex = 5ex + C
It is given that,
f(7) = 5e7 + C
⇒40 + 5e7 = 5e7 + C
⇒ C = 40
f(x) = 5ex + 40
⇒f(5) = 5e5 + 40
Let’s see some sample problems with these concepts.
Sample Problems
Question 1: Find the integral for the given function f(x),
f(x) = sin(x) + 2
Solution:
Given f(x) = sin(x) + 2
sin(x) is a standard function, and it’s anti-derivative is known.
∫f(x)dx
⇒ ∫(sin(x) + 2)dx
Using the property 2 mentioned above,
∫sin(x)dx + ∫2dx
⇒-cos(x) + 2x + C
Question 2: Find the integral for the given function f(x),
f(x) = 5ex
Solution:
Given f(x) = 5ex
ex is a standard function, and it’s anti-derivative is known.
∫f(x)dx
⇒∫5exdx
Using the property 1 mentioned above,
5∫exdx
⇒5ex + C
Question 3: Find the integral for the given function f(x),
f(x) = x-1
Solution:
Given f(x) = x-1
Using the reverse power rule
∫f(x)dx
⇒∫(x – 1)dx
Using the property 1 mentioned above,
∫xdx – ∫1dx
⇒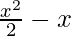
Question 4: Find the integral for the given function f(x),
f(x) = sin(x) + cos(x)
Solution:
Given f(x) = sin(x) + cos(x)
sin(x) and cos(x) are standard functions, and its integral is known.
\int f(x)dx
⇒∫(sin(x) + cos(x))dx
Using the properties 1 and 2 mentioned above,
∫sin(x)dx + ∫cos(x)dx
⇒-cos(x) + sin(x) + C
Question 5: Given f'(x) = ex and f(2) = 5 + e2 find the value of f(4).
Solution:
f(x) = ∫f'(x) = ∫ex = ex + C
It is given that,
f(2) = e2 + C
⇒5 + e2 = e2 + C
⇒ C =5
f(x) = ex +5
⇒f(4) = e4 +5
Question 6: Given f'(x) = 6x2 and f(2) = 12. The goal is to find out f(-1).
Solution:
Let’s re-write the given functions,
f(x) = ∫f'(x) = ∫6x2 = 2x3 + C
It is given that,
f(2) = 12
⇒ 2(2)3 + C = 12
⇒C = -4
Plugging in the value of C in the equation of f(x),
f(x) = 2x3 -4
f(-1) = 2(-1)3 -4
f(-1) = -6
Question 7: Given f'(x) = 6x2 + 4x and f(2) = 12. The goal is to find out f(-1).
Solution:
Let’s re-write the given functions,
f(x) = ∫f'(x) = ∫6x2 + 4x = 2x3 + 2x2 + C
It is given that,
f(2) = 12
⇒223 + 222 + C = 12
⇒C = -12
Plugging in the value of C in the equation of f(x),
f(x) = 2x3 + 2x2 -12
f(-1) = 2(-1)3 + 2(-1)2 – 12
f(-1) = -12
Share your thoughts in the comments
Please Login to comment...