Trapezoidal Rule

Last Updated : 24 Nov, 2023

The trapezoidal rule is one of the fundamental rules of integration which is used to define the basic definition of integration. It is a widely used rule and the Trapezoidal rule is named so because it gives the area under the curve by dividing the curve into small trapezoids instead of rectangles.

Generally, we find the area under the curve by dividing the area into smaller rectangles and then finding the sum of all the rectangles, but in the trapezoidal rule the area under the curve is divided into trapezoids, and then their sum is calculated. The trapezoidal rule is used to find the value of the definite integrals in numerical analysis. This rule is also called the trapezoid rule or the trapezium rule. Let us learn more about the trapezoidal rule, its formula and proof, example, and others in detail in this article.

What is the Trapezoidal Rule?

The trapezoidal rule is a rule which is used to find the value of the definite integral of the form ^b∫_a f(x) dx. We know that the value of the definite integral ^b∫_a f(x) dx is the area enclosed under the curve y = f(x) and the x-axis in the interval a and b on the x-axis. We calculate this area by dividing the complete area into several small rectangles and then finding their sum.

In the Trapezoidal rule as the name suggest the area under the curve is divided into several trapezoids and then their sum is found to get the area of the curve. The trapezoidal rule does not provide the best approximation of the area under the curve than the Simpson’s Rule but still, its result is precise enough and this rule is a widely used rule in calculus.

Trapezoidal Rule Formula

The trapezoidal rule formula is the formula that is used to find the area under the curve. Now to find the area under the curve using the Trapezoidal Rule,

Let y = f(x) be a continuous curve defined on the closed interval [a, b]. Now we divide the closed interval [a, b] into n equal subintervals, with each having the width of,

Δx = (b – a)/n

Such that,

a = x₀ < x₁ < x₂ < ⋯ < x_n = b

Now using the Trapezoidal rule formula we can find the area under the curve as,

∫^b_a f(x) dx = Area Under the Curve = (Δx/2) [y₀ + 2 (y₁ + y₂ + y₃ + ….. + y_n-1) + y_n]

where, y₀, y₁, y₂, …. y_n are the values of function at x = 1, 2, 3, ….., n respectively.

Derivation of Trapezoidal Rule Formula

The Trapezoidal Rule formula for calculating the area under the curve is derived by dividing the area under the curve into several trapezoids and then finding their sum.

Statement:

Let f(x) be a continuous function defined on the interval (a, b). Now we divide the intervals (a, b) into n equal sub-intervals where the width of each interval is,

Δx = (b – a)/n

such that a = x₀ < x₁ < x₂ < x₃ <…..< x_n = b

Then the Trapezoidal Rule formula is,

∫^b_af(x) dx ≈ △x/2 [f(x₀) + 2f(x₁) + 2f(x₂) +….2f(x_n-1) + f(x_n)]

where, x_i = a + i△x

If n → ∞, the R.H.S of the expression gives the definite integral $\int_{a}^{b}f(x) dx$

Proof:

This formula is proved by dividing the area under the given curve as shown in the above figure into various trapezoids. The first trapezoid has a height Δx and the length of parallel bases are f(x₀) and f(x₁)

The area of the first trapezoid = (1/2) Δx [f(x₀) + f(x₁)]

Similarly, the area of the remaining trapezoids are (1/2)Δx [f(x₁) + f(x₂)], (1/2)Δx [f(x₂) + f(x₃)], and so on.

Now we can say that,

∫^b_a f(x) dx ≈ (1/2)Δx (f(x₀)+f(x₁) ) + (1/2)Δx (f(x₁)+f(x₂) ) + (1/2)Δx (f(x₂)+f(x₃) ) + … + (1/2)Δx (f(x_n-1) + f(x_n) )

After simplifying we get,

∫^b_a f(x) dx≈ (Δx/2) (f(x₀)+2 f(x₁)+2 f(x₂)+2 f(x₃)+ … +2f(x_n-1) + f(x_n))

Thus, the trapezoidal rule is proved.

How to Apply Trapezoidal Rule?

The trapezoidal rule finds the area under the curve by dividing the area under the curve into various trapezoids and then find the sum of all the trapezoids. The trapezoidal rule is not the perfect approximation of the value of the definite integral as it uses the quadratic approximation.

We have to find the value of the definite integral, ∫^b_a f(x) dx. The value of the definite integral can be calculated using the trapezoidal rule by following the steps below,

Step 1: Mark the value of sub-intervals, “n” and intervals “a” and “b”.

Step 2: Find the width of sub-interval (△x) using the formula △x = (b – a)/n

Step 3: Put all the values in the trapezoidal rule formula and find the approximate area of the given curve which represents the definite integral ∫^b_a f(x) dx

∫^b_a f(x) dx ≈ (Δx/2) (f(x₀)+2 f(x₁)+2 f(x₂)+2 f(x₃)+ … +2f(x_n-1) + f(x_n))

where, x_i = a + i△x

Summation Notation of Trapezoidal Rule

We know that the area of a trapezoid is basically the average of the lengths of the parallel sides multiplied by the height. So, in this case, consider a trapezoid for the i^th interval,

$A_{i} = \frac{f(x_{i}) + f(x_{i-1})}{2}\Delta x$

Since the total area is the sum of all the areas,

A = A₁ + A₂ + ….+ A_n

⇒ A = $\sum_{i = 1}^{i = n} A_{i}$

⇒ A = $\sum_{i = 1}^{i = n}\frac{f(x_{i}) + f(x_{i-1})}{2}\Delta x$

This is called the sigma notation or summation notation of the trapezoid sums.

Riemann Sums

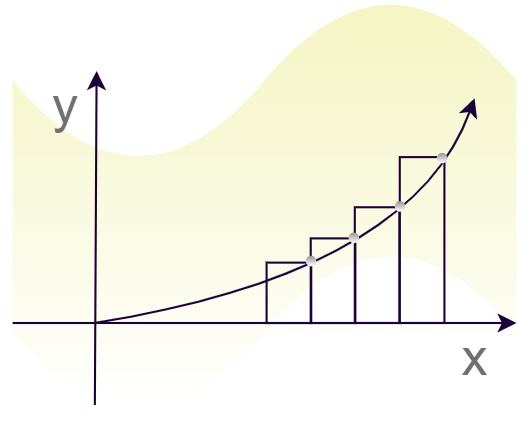
The Riemann sums up work on the idea of diving the area under the curve into different rectangular parts. As the number of rectangles increases, the area becomes closer and closer to the current area. In the figure shown below, there is a function f(x). The area under this function is divided into many rectangles. The total area under the curve is the sum of the areas of all the rectangles.

Notice that in the above figure, the right end of the rectangles touches the curve. This is called right-Riemann sums.

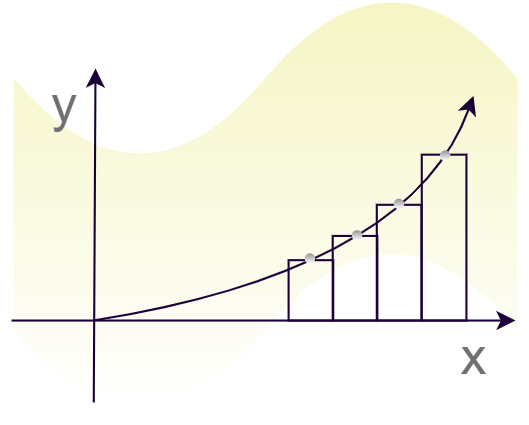
In another case, when the left end of the rectangles touches the curve as shown in the image below, they are called left Riemann sums.

Let’s say Δx is the width of the interval width n is the number of intervals as stated above. Then the area of the curve represented by the sum is given by,

$\bold{A = \sum^{i = n}_{i = 1}A_{i} = \sum^{i = n}_{i = 1}f(x_{i})\Delta x}$

Middle Point Sums

In the Riemann sums, either the left end or the right end of the rectangle touches the curve. In this case, the middle point of the rectangle touches the curve. Everything else is the same as Riemann sums. The figure below shows the function f(x) and different rectangles in the middle point sums.

Let’s say A_idenotes the area of the i^th rectangle. The area of this rectangle in this case will be,

$A_{i} = f(\frac{x_i + x_{i-1}}{2}) \Delta x$

Now, the total area in the summation notation will be given by,

$\bold{A = \sum^{i = n}_{i = 1}A_{i} = \sum^{i = n}_{i = 1}f(\frac{x_{i} + x_{i-1}}{2})\Delta x}$

Read More,

Integration Formulas
Integration by Parts
Differentiation and Integration Formula

Solved Example on Trapezoidal Rule

Example 1: Find the area enclosed by the function f(x) between x = 0 to x = 4 with 4 intervals.

f(x) = 4

Solution:

Here a = 0, b = 4 and n = 4.

$\Delta x= \frac{b - a}{n} \\ = \Delta x = \frac{4 - 0}{4} \\ = \Delta x = 1$

$x_{i} = a + i\Delta x \\ = x_{i} = 0 + i \\ = x_{i} = i$

The trapezoidal rule for n = 4 is,

$T_n = \frac{\Delta x}{2}(f(x_0) + 2f(x_1) + 2f(x_2) + 2f(x_3) + f(x_4))$

Substituting the values in this equation,

$T_n = \frac{\Delta x}{2}(f(x_0) + 2f(x_1) + 2f(x_2) + 2f(x_3) + f(x_4)) \\ = \frac{1}{2}(f(0) + 2f(1) + 2f(2) + 2f(3) + f(4)) = \frac{1}{2}(4 + 2(4) + 2(4) + 2(4) + 4) \\ = 16$

Example 2: Find the area enclosed by the function f(x) between x = 0 to x = 3 with 3 intervals.

f(x) = x

Solution:

Here a = 0, b = 3 and n = 3.

$\Delta x= \frac{b - a}{n} \\ = \Delta x = \frac{3 - 0}{3} \\ = \Delta x = 1$

$x_{i} = a + i\Delta x \\ = x_{i} = 0 + i \\ = x_{i} = i$

The trapezoidal rule for n = 3 is,

$T_n = \frac{\Delta x}{2}(f(x_0) + 2f(x_1) + 2f(x_2) + f(x_3))$

Substituting the values in this equation,

$T_n = \frac{\Delta x}{2}(f(x_0) + 2f(x_1) + 2f(x_2) + f(x_3)) \\ \Rightarrow T_n= \frac{1}{2}(f(0) + 2f(1) + 2f(2) + f(3)) \\ \Rightarrow T_n= \frac{1}{2}(0 + 2 + 2(2) + 2(3))\\ \Rightarrow T_n= \frac{1}{2}(2 + 4 + 6) = 6$

Example 3: Find the area enclosed by the function f(x) between x = 0 to x = 2 with 2 intervals.

f(x) = 2x

Solution:

Here a = 0, b = 2 and n = 2.

$\Delta x= \frac{b - a}{n} \\ = \Delta x = \frac{2 - 0}{2} \\ = \Delta x = 1$

$x_{i} = a + i\Delta x \\ = x_{i} = 0 + i \\ = x_{i} = i$

The trapezoidal rule for n = 2 is,

$T_n = \frac{\Delta x}{2}(f(x_0) + 2f(x_1) + f(x_2))$

Substituting the values in this equation,

$T_n = \frac{\Delta x}{2}(f(x_0) + 2f(x_1) + f(x_2)) \\ \Rightarrow T_n= \frac{1}{2}(f(0) + 2f(1) + f(2))\\ \Rightarrow T_n= \frac{1}{2}(0 + 2(2) + 1(4))\\ \Rightarrow T_n= \frac{1}{2}(8) \\ = 4$

Example 4: Find the area enclosed by the function f(x) between x = 0 to x = 3 with 3 intervals.

f(x) = x²

Solution:

Here a = 0, b = 3 and n = 3.

$\Delta x= \frac{b - a}{n} \\ = \Delta x = \frac{3 - 0}{3} \\ = \Delta x = 1$

$x_{i} = a + i\Delta x \\ = x_{i} = 0 + i \\ = x_{i} = i$

The trapezoidal rule for n = 3 is,

$T_n = \frac{\Delta x}{2}(f(x_0) + 2f(x_1) + 2f(x_2) + f(x_3))$

Substituting the values in this equation,

$T_n = \frac{\Delta x}{2}(f(x_0) + 2f(x_1) + 2f(x_2) + f(x_3)) \\ \Rightarrow T_n= \frac{1}{2}(f(0) + 2f(1) + 2f(2) + f(3)) \\ \Rightarrow T_n= \frac{1}{2}(0 + 2(1) + 2(4) + 2(9))\\ \Rightarrow T_n= \frac{1}{2}(2 + 8 + 18) = 14$

Example 5: Find the area enclosed by the function f(x) between x = 0 to x = 4 with 4 intervals.

f(x) = x³ + 1

Solution:

Here a = 0, b = 4 and n = 4.

$\Delta x= \frac{b - a}{n} \\ = \Delta x = \frac{4 - 0}{4} \\ = \Delta x = 1$

$x_{i} = a + i\Delta x \\ = x_{i} = 0 + i \\ = x_{i} = i$

The trapezoidal rule for n = 4 is,

$T_n = \frac{\Delta x}{2}(f(x_0) + 2f(x_1) + 2f(x_2) + 2f(x_3) + f(x_4))$

Substituting the values in this equation,

$T_n = \frac{\Delta x}{2}(f(x_0) + 2f(x_1) + 2f(x_2) + 2f(x_3) + f(x_4)) \\ \Rightarrow T_n = \frac{1}{2}(f(0) + 2f(1) + 2f(2) + 2f(3) + f(4)) \\ \Rightarrow T_n= \frac{1}{2}(1 + 2(2) + 2(9) + 2(28) + (65) )\\ \Rightarrow T_n= \frac{1}{2}(1 + 4 + 18 + 56 + 65) \\ \Rightarrow T_n= 72$

Example 6: Find the area enclosed by the function f(x) between x = 0 to x = 4 with 4 intervals.

f(x) = e^x

Solution:

Here a = 0, b = 4 and n = 4.

$\Delta x= \frac{b - a}{n} \\ = \Delta x = \frac{4 - 0}{4} \\ = \Delta x = 1$

$x_{i} = a + i\Delta x \\ = x_{i} = 0 + i \\ = x_{i} = i$

The trapezoidal rule for n = 4 is,

$T_n = \frac{\Delta x}{2}(f(x_0) + 2f(x_1) + 2f(x_2) + 2f(x_3) + f(x_4))$

Substituting the values in this equation,

$T_n = \frac{\Delta x}{2}(f(x_0) + 2f(x_1) + 2f(x_2) + 2f(x_3) + f(x_4)) \\ \Rightarrow T_n= \frac{1}{2}(f(0) + 2f(1) + 2f(2) + 2f(3) + f(4))\\ \Rightarrow T_n= \frac{1}{2}(e^0 + 2e + 2e^2 + 2e^3 + e^4 )\\ \Rightarrow T_n= \frac{1}{2} + e + e^2 + e^3 + \frac{e^4}{2}$

Applications of Trapezoid Rule

Numerical Integration:

The primary application of the trapezoidal rule is in approximating definite integrals. It’s used when the integration of a function is challenging, and a numerical approach is more feasible. The trapezoidal rule is often part of more advanced numerical integration techniques.

Physics and Engineering:

In physics and engineering, the trapezoidal rule can be applied to calculate quantities such as displacement, velocity, and acceleration. For example, when experimental data is collected at discrete time intervals, the trapezoidal rule can be used to estimate the area under the curve, providing an approximation of the integral.

Economics and Finance:

The trapezoidal rule can be applied in financial modeling to estimate the present value of future cash flows. This is especially useful in discounted cash flow (DCF) analysis, where the goal is to calculate the net present value of an investment.

Statistics:

In statistics, the trapezoidal rule can be used to estimate the area under probability density functions or cumulative distribution functions. This is particularly useful in cases where the exact form of the distribution is unknown or complex.

FAQs on Trapezoidal Rule

Q1: What is Trapezoidal Rule?

Answer:

The trapezoidal rule is the rule that is used to find the definite integral it divides the area under the curve into several trapezoids and then their individual area is found and then the sum is calculated to get the value of the definite integral.

Q2: What is the Trapezoidal Rule Formula?

Answer:

The trapezoidal rule formula is,

∫^b_a f(x) dx = (Δx/2) (f(x₀)+2 f(x₁)+2 f(x₂)+2 f(x₃)+ … +2f(x_n-1) + f(x_n))

Q3: Why is it Called Trapezoidal Rule Formula?

Answer:

Trapezoidal Rule Formula is called the trapezoidal rule because it divides the area under the curve into several trapezoids and then their area is calculated by finding the sum of the trapezoids.

Q4: What is the Difference Between Trapezoidal Rule and Riemann Sums Rule?

Answer:

The major difference between the Trapezoidal rule and Riemann Sums rule is, as the trapezoidal rule divides the area under the curve as the trapezoids and then finds the area by taking their sum whereas, the Riemann Sums divides the area under the curve as the trapezium and then finds the area by taking their sum.

Suggest improvement

Riemann Sums in Summation Notation

Definite Integral as the Limit of a Riemann Sum

Share your thoughts in the comments

Chapter 1: Relations and Functions

Chapter 2: Inverse Trigonometric Functions

Chapter 3: Matrices

Chapter 4: Determinants

Chapter 5: Continuity and Differentiability

Chapter 6: Applications of Derivatives

Chapter 7: Integrals

Chapter 8: Applications of Integrals

Chapter 9: Differential Equations

Chapter 10: Vector Algebra

Chapter 11: Three-dimensional Geometry

Chapter 12: Linear Programming

Chapter 13: Probability

Trapezoidal Rule

What is the Trapezoidal Rule?

Trapezoidal Rule Formula

Derivation of Trapezoidal Rule Formula

Statement:

Proof:

How to Apply Trapezoidal Rule?

Summation Notation of Trapezoidal Rule

Riemann Sums

Middle Point Sums

Solved Example on Trapezoidal Rule

Example 1: Find the area enclosed by the function f(x) between x = 0 to x = 4 with 4 intervals.

Example 2: Find the area enclosed by the function f(x) between x = 0 to x = 3 with 3 intervals.

Example 3: Find the area enclosed by the function f(x) between x = 0 to x = 2 with 2 intervals.

Example 4: Find the area enclosed by the function f(x) between x = 0 to x = 3 with 3 intervals.

Example 5: Find the area enclosed by the function f(x) between x = 0 to x = 4 with 4 intervals.

Example 6: Find the area enclosed by the function f(x) between x = 0 to x = 4 with 4 intervals.

Applications of Trapezoid Rule

Numerical Integration:

Physics and Engineering:

Economics and Finance:

Statistics:

FAQs on Trapezoidal Rule

Q1: What is Trapezoidal Rule?

Q2: What is the Trapezoidal Rule Formula?

Q3: Why is it Called Trapezoidal Rule Formula?

Q4: What is the Difference Between Trapezoidal Rule and Riemann Sums Rule?

Please Login to comment...

Similar Reads

What kind of Experience do you want to share?