Definite integrals are an important part of calculus. They are used to calculate the areas, volumes, etc of arbitrary shapes for which formulas are not defined. Analytically they are just indefinite integrals with limits on top of them, but graphically they represent the area under the curve. The limits denote the boundaries between which the area should be calculated. These concepts hold a lot of importance in the field of electrical engineering, robotics, etc. For defining integrals, Riemann sums are used in which we calculate the area under any curve using infinitesimally small rectangles. Let’s look at this interpretation of definite integrals in detail.
Riemann Approximation
Riemann’s sums are a method for approximating the area under the curve. The intuition behind it is, if we divide the area into very small rectangles, we can calculate the area of each rectangle and then add them to find the area of the total region. This is the same intuition as the intuition behind the definite integrals. So, these sums can be also be used to approximate and define the definite integrals. Definite integrals are nothing but integrals with limits, they are used to find the areas, volumes, etc under arbitrary curve shapes. Consider the figure below, the goal is to calculate the area enclosed by this curve between x = a and x = b and the x-axis.

Now let’s start with dividing the given area into a number of rectangles, assuming the area is divided into ‘n’ rectangles of equal width. Notice that these rectangles do not cover the full area, so it is an approximation of the area. But as the number of rectangles increases, the approximation comes closer and closer to the actual area.

In the definite integral notation, this area will be represented as,
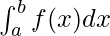
This area can be approximated by divided the area under the curve into n equally sized rectangles. So, the interval [a, b] is divided into n-subintervals defined by the points.
a = x0 < x1 < x2 < …. xn-2< xn-1 < xn = b
Then, the n intervals are,
[x0, x1], [x1, x2], …. [xn-1, xn]
So, for the ith rectangle, the width will be, [xi-1, xi].
The area for ith rectangle Ai = f(xi)(xi — xi-1)
So, the total area will be 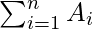
This sum is called the Riemann sum. Since the height of the rectangle is determined by the right limit of the interval, this is called the right-Riemann sum. The figure below shows the left-Riemann sum.

Summation Notation
The steps given below should be followed to find the summation notation of the riemann integral.
Step 1: Find out the width of each interval. Let’s denote the width of interval with 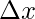
Step 2: Let xi denote the right-endpoint of the rectangle xi = a + 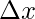 .i
.i
Step 3: Define the area of each rectangle.
Step 4: Sum the areas
Let’s say the goal is to calculate the area under the graph of the function f(x) = x3, the area will be calculated between the limits x = 0 to x = 4.
Divide the interval into four equal parts, the intervals will be [0, 1], [1, 2], [2, 3] and [3, 4].
The riemann sum then, can be written as follows,
A(1) + A(2) + A(3) + A(4) = 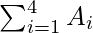
Let’s calculate the right sum Riemann sum. Assume xi denotes the right endpoint of the ith rectangle.
So, the formula for xi = i. Now, the value of the function at these points becomes,
f(xi) = (i)3
So, A(i) = (height)(width)
= (i)3
The Riemann sum becomes,
A(1) + A(2) + A(3) + A(4) = 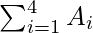
⇒ A(1) + A(2) + A(3) + A(4) = 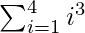
So, this way almost all the Riemann sums can be represented in a sigma notation.
Let’s work out some problems with these concepts.
Sample Problems
Question 1: Choose which type of the Riemann integral is shown below in the figure.

- Left-Riemann Sum
- Right-Riemann Sum
- Mid-point Riemann Sum
Solution:
Since the values of the intervals are decided according to the left-end point of the interval. This is a left-Riemann Sum
Answer-(1).
Question 2: Calculate the Left-Riemann Sum for the function given in the figure above.
Solution:
Dividing the interval into four equal parts that is n = 4. The width of each interval will be,
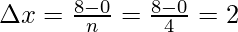
x0 = 0, x1 = 1, x2 = 2, x3 = 0 and x4 = 0
The value of the function in each interval will be the value of the function at the right-end of the interval.
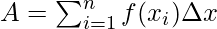
⇒A = 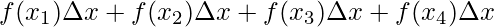
⇒A = 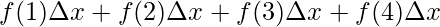
⇒A = f(1)(2) + f(2)(2)+ f(3)(2) + f(4)(2)
⇒A = (f(1) + f(2) + f(3)+ f(4))(2)
⇒A = (1 + 2 + 3+ 4)(2)
⇒A = (10)(2)
⇒A = 20
Question 3: Consider a function f(x) = 5 – 2x, its area is calculated from riemann sum from x = 0 to x = 4, the whole area is divided into 4 rectangles. Find the riemann sum in sigma notation
Answer:
Step (i): Calculate the width
The whole length is divided into 4 equal parts,
xi = 0 and xl = 4,
Width of an interval is given by = 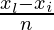
Where xi = initial point, and xl – last point and n= number of parts
n = 4
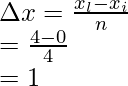
Step(ii):
a = 0,
xi = 0 + 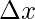 i
i
⇒ xi = i
Step (iii):
Ai = Height x Width
= f(xi) 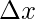
= (5 – 2i)(1)
= 5 – 2i
Total Area = A(1) + A(2) + A(3) + A(4) + A(5)
= 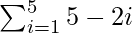
Question 4: Consider a function f(x) = x2, its area is calculated from riemann sum from x = 0 to x = 3, the whole area is divided into 3 rectangles. Find the riemann sum in sigma notation
Answer:
Step (i): Calculate the width
The whole length is divided into 3 equal parts,
xi = 0 and xl = 3,
Width of an interval is given by = 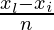
Where xi = initial point, and xl – last point and n= number of parts
n = 3
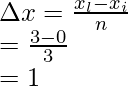
Step(ii):
a = 0,
xi = 0 + 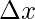 i
i
⇒ xi = i
Step (iii)
Ai = Height x Width
= f(xi) 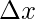
= (i2)
Total Area = A(1) + A(2) + A(3) + A(4) + A(5)
= 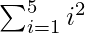
Question 5: Consider a function f(x) = √x, its area is calculated from riemann sum from x = 0 to x = 4, the whole area is divided into 4 rectangles. Find the riemann sum in sigma notation
Answer:
Step (i): Calculate the width
The whole length is divided into 4 equal parts,
xi = 0 and xl = 4,
Width of an interval is given by = 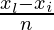
Where xi = initial point, and xl – last point and n= number of parts
n = 4
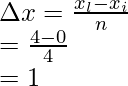
Step(ii):
a = 0,
xi = 0 + 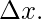 i
i
⇒ xi = i
Step (iii)
Ai = Height x Width
= f(xi) 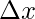
= (√i)(1)
= √i
Total Area = A(1) + A(2) + A(3) + A(4)
= 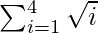
Question 6: Consider a function f(x) = x2, its area is calculated from riemann sum from x = 0 to x = 2, the whole area is divided into 2 rectangles. Find the riemann sum in sigma notation
Answer:
Step (i): Calculate the width
The whole length is divided into 2 equal parts,
xi = 0 and xl = 2,
Width of an interval is given by = 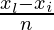
Where xi = initial point, and xl – last point and n= number of parts
n = 2
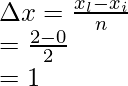
Step(ii):
a = 0,
xi = 0 + 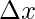 i
i
⇒ xi = i
Step (iii):
Ai = Height x Width
= f(xi) 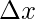
= (i2)(1)
= i2
Total Area = A(1) + A(2) + A(3) + A(4)
= 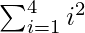
Question 7: Consider a function f(x) = 3(x + 3), its area is calculated from riemann sum from x = 0 to x = 6, the whole area is divided into 6 rectangles. Find the riemann sum in sigma notation
Answer:
Step (i): Calculate the width
The whole length is divided into 4 equal parts,
xi = 0 and xl = 6,
Width of an interval is given by = 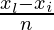
Where xi = initial point, and xl – last point and n= number of parts
n = 6
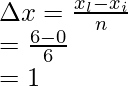
Step(ii):
a = 0,
xi = 0 + 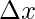 i
i
⇒ xi = i
Step (iii):
Ai = Height x Width
= f(xi) 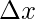
= (3(i + 3))(1)
= 3(i + 3)
Total Area = A(1) + A(2) + A(3) + A(4)
= 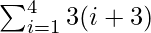
Like Article
Suggest improvement
Share your thoughts in the comments
Please Login to comment...