Class 12 RD Sharma Solutions – Chapter 29 The Plane – Exercise 29.14
Last Updated :
11 Feb, 2021
Question 1. Find the shortest distance between the lines 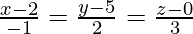 and
and 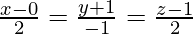 .
.
Solution:
Let us consider
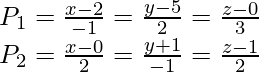
According to the equations line P1 passes through the point P(2, 5, 0)
And the equation of a plane containing line P2 is
a(x – 0) + b(y + 1) + c(z – 1) = 0 -(1)
Where 2a – b + 2c = 0
If it is parallel to line P1 then
-a + 2b + 3c = 0
So,
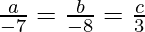
Now, substitute the value of a, b, c in the eq(1) we get
a(x – 0) + b(y + 1) + c(z – 1) = 0
-7(x – 0) – 8(y + 1) + 3(z – 1) = 0
-7x – 8y – 8 + 3z – 3 = 0
7x + 8y – 3z + 11 = 0 -(2)
So, this is the equation of the plane that contain line P2 and parallel to line P1.
Hence, the shortest distance between P1 and P2 = Distance between point P(2, 5, 0) and plane (2)
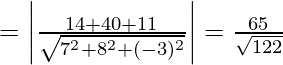
Question 2. Find the shortest distance between the lines 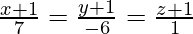 and
and 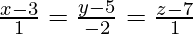 .
.
Solution:
Let us consider
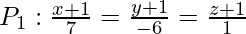
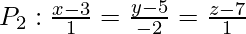
Let us assume the equation of the plane containing P1 is a(x + 1) + b(y + 1) + c(z+1) = 0
Plane is parallel to P1 = 7a – 6b + c = 0 -(1)
Plane is parallel to P2 = a – 2b + c = 0 -(2)
On solving eq(1) and eq(2), we get,
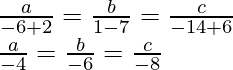
The equation of the plane is -4(x + 1) – 6(y + 1) – 8(z + 1) = 0
Final equation of plane is 4(x + 1) + 6(y + 1) + 8(z + 1) = 0
Question 3. Find the shortest distance between the lines 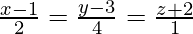 and 3x – y – 2z + 4 = 0, 2x + y + z + 1 = 0.
and 3x – y – 2z + 4 = 0, 2x + y + z + 1 = 0.
Solution:
The equation of a plane containing the line 3x – y – 2z + 4 = 0, 2x + y + z + 1 = 0 is
x(2λ + 3) + y(λ – 1) + z(λ – 2) + λ + 4 = 0 -(1)
If it is parallel to the line 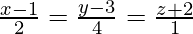 then,
then,
2(2λ + 3) + 4(λ – 1) + (λ – 2) = 0
λ = 0
On putting λ = 0 in eq(1) we get,
3x – y – 2z + 4 = 0 -(2)
As this equation of the plane consist the second line and parallel to the first line.
It is clear that the line 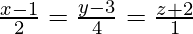 passes through the point (1, 3, -2)
passes through the point (1, 3, -2)
So, the shortest distance ‘D’ between the given lines is equal to the
length of perpendicular from point (1, 3, -2) on the plane (2)
D = 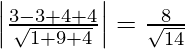
Share your thoughts in the comments
Please Login to comment...