Question 7. Find the equation of the normal to the curve ay2 = x3 at the point (am2, am3).
Solution:
We have,
ay2 = x3
On differentiating both sides w.r.t. x, we get
2aydy/dx = 3x2
dy/dx = 3x2/2ay
Slope of tangent = 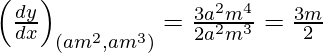
Given (x1, y1) = (am2, am3)
The equation of normal is,
y – y1 = -1/m (x – x1)
y – a m3 = -2m/3 (x – am2)
3my – 3am4 = – 2x + 2am2
2x + 3my – am2 (2 + 3m2) = 0
Question 8. The equation of the tangent at (2, 3) on the curve y2 = ax3 + b is y = 4x − 5. Find the values of a and b.
Solution:
We have,
y2 = ax3 + b
On differentiating both sides w.r.t. x, we get
2y dy/dx = 3ax2
dy/dx = 3ax2/2y
Slope of tangent, m = 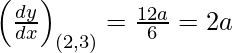
The equation of tangent is given by y – y1 = m (tangent) (x – x1)
Now compare the slope of a tangent with the given equation
2a = 4
a = 2
Now (2, 3) lies on the curve, these points must satisfy
32 = 2 (23) + b
b = – 7
Question 9. Find the equation of the tangent line to the curve y = x2 + 4x − 16 which is parallel to the line 3x − y + 1 = 0.
Solution:
We have,
y = x2 + 4x − 16
Let (a, b) be the point of intersection of both the curve and the tangent.
Since (a, b) lies on curve, we get
b = a2 + 4a − 16
Now, x2 + 4x − 16
dy/dx = 2x + 4
Slope of tangent = 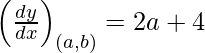
Given that the tangent is parallel to the line we have,
Slope of tangent = Slope of the given line
=> 2a + 4 = 3
=> 2 a = -1
=> a = -1/2
From eq(1), we get
b = 1/4 – 2 – 16 = -71/4
Now, slope of tangent, m = 3
(a, b) = (-1/2, -71/4)
The equation of tangent is,
y – y1 = m (x – x1)
y + 71/4 = 3 (x + 1/2)
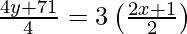
4y + 71 = 12x + 6
12x – 4y – 65 = 0
Question 10. Find an equation of normal line to the curve y = x3 + 2x + 6 which is parallel to the line x+ 14y + 4 = 0.
Solution:
We have,
y = x3 + 2x + 6
Let (a, b) be a point on the curve where we need to find the normal.
Slope of the given line = -1/14
Since the point lies on the curve, we get
b = a3 + 2a + 6
Now, y = x3 + 2x + 6
dy/dx = 3 x2 + 2
Slope of the tangent, m = 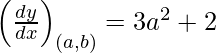
Slope of the normal = 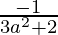
Given that, slope of the normal = slope of the given line, we have
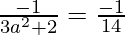
3a2 + 2 = 14
3a2 = 12
a2 = 4
a = ±2
So, b = 18 or -6.
And slope of the normal = -1/14
When a = 2 and b = 18, we have
y – y1 = m (x – x1)
y – 18 = -1/14 (x – 2)
14y – 252 = -x + 2
x + 14y – 254 = 0
When a = -2 and b = -6, we have
y – y1 = m (x – x1)
y + 6 = -1/14 (x + 2)
14y + 84 = -x – 2
x + 14y + 86 = 0
Question 11. Determine the equation(s) of tangent (s) line to the curve y = 4x3 − 3x + 5 which are perpendicular to the line 9y + x + 3 = 0.
Solution:
Let (a, b) be a point on the curve where we need to find the tangent(s).
Slope of the given line = -1/9
Since, tangent is perpendicular to the given line,
Slope of the tangent = 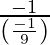 = 9
= 9
Hence, b = 4 a3 – 3 a + 5
Now, y = 4 x3 – 3x + 5
dy/dx = 12 x2 – 3
Slope of the tangent = 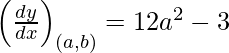
Given that, slope of the tangent = slope of the perpendicular line
12a2 – 3 = 9
12a2 = 12
a2 = 1
a = ±1
So, b = 6 or 4.
Thus, slope of tangent = 9.
When a = 1 and b = 6, we have
y – y1 = m (x – x1)
y – 6 = 9 (x – 1)
y – 6 = 9x – 9
9x – y – 3 = 0
When a = -1 and b = 4, we have
y – y1 = m (x – x1)
y – 4 = 9 (x + 1)
y – 4 = 9x + 9
9x – y + 13 = 0
Question 12. Find the equation of a normal to the curve y = x loge x which is parallel to the line 2x − 2y + 3 = 0.
Solution:
Slope of the given line is 1.
Let (a, b) be the point where the tangent is drawn to the curve.
Hence, b = a loge a . . . . (1)
Now, y = x loge x
dy/dx = x × 1/x + loge x(1) = 1 + loge x1
Slope of tangent = 1 + log a
Slope of normal = 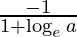
Given that, slope of normal = slope of the given line.
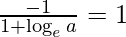
=> -1 = 1 + log a
=> – 2 = log a
=> a = e-2
From (1), we have
Now, b = e-2 (-2) = -2 e-2
Given, (x1, y1) = (e-2, -2 e-2)
The equation of normal is,
y + 2/e2 = 1(x – 1/e2)
y + 2/e2 = x – 1/e2
x – y = 3/e2
Question 13. Find the equation of the tangent line to the curve y = x2 − 2x + 7
(i) which is parallel to the line 2x − y + 9 = 0?
Solution:
We have, y = x2 − 2x + 7
On differentiating both sides, we get
dy/dx = 2x – 2
The equation of the line is 2x – y + 9 = 0
So the slope of line is 2.
According to the question,
=> 2x – 2 = 2
=> 2x = 4
=> x = 2
=> y = 22 − 2(2) + 7 = 4 – 4 + 7 = 7
As (x1, y1) is (2, 7), the equation of tangent is,
y – 7 = 2(x – 2)
y – 7 = 2x – 4
y – 2x – 3 = 0
(ii) which is perpendicular to the line 5y − 15x = 13.
Solution:
We have, y = x2 − 2x + 7
On differentiating both sides, we get
dy/dx = 2x – 2
The equation of the line is 5y − 15x = 13.
=> y = 3x + 13/5
So the slope of line is 3.
According to the question,
=> 2x – 2= -1/3
=> 6x – 6 = -1
=> x = 5/6
And y = 217/36.
As (x1, y1) is (5/6, 217/36), the equation of tangent is,
y – y1 = m (x – x1)
y – 217/36 = (-1/3) (x – 5/6)
36y -217 = -12x + 10
36y + 12x – 227 = 0
Question 14. Find the equations of all lines having slope 2 and that are tangent to the curve y = 1/x – 3, x ≠ 3.
Solution:
Let (a , b) be the point where the tangent is drawn to this curve.
Since, the point lies on the curve, hence b = 1/(a – 3)
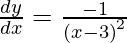
Slope of tangent, m = 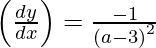
Slope of the tangent} = 2
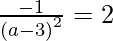
(a – 3)2 = – 2
a – 3 = √-2, which does not exist because 2 is negative.
So, there does not exist any such tangent.
Question 15. Find the equations of all lines of slope zero and that are tangent to the curve 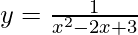 .
.
Solution:
Slope of the given tangent is 0.
Let (a, b) be a point where the tangent is drawn to the curve.
Since, the point lies on the curve, hence b =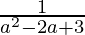 . . . . (1)
. . . . (1)
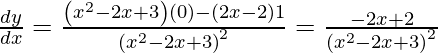
Slope of tangent = 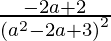
Given that, slope of tangent = slope of the given line,
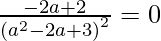
=> -2 a + 2 = 0
=> 2a = 2
=> a = 1
From (1), we get
Now, b = 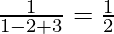
(a, b) = (1, 1/2)
The equation of tangent is,
y – y1 = m (x – x1)
y – 1/2 = 0 (x – 1)
y = 1/2
Question 16. Find the equation of the tangent to the curve 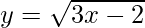 which is parallel to the 4x − 2y + 5 = 0.
which is parallel to the 4x − 2y + 5 = 0.
Solution:
We have,
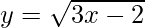
Let (a, b) be the point where the tangent is drawn to the curve y = 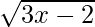
On differentiating both sides, we get
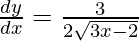
Slope of tangent at (a, b) = 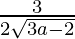
Slope of line 4x − 2y + 5 = 0 is 2.
Given that, slope of tangent = slope of the given line
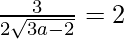
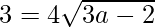
9 = 16 (3a – 2)
9/16 = 3a – 2
3a = 9/16 + 2
a = 41/48
Now, b = 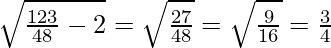
Therefore, (a, b) = (41/48, 3/4)
The equation of tangent is,
y – y1 = m (x – x1)
y – 3/4 = 2 (x – 41/48)
(4y – 3)/4 = 2 (48x – 41)/48
24y – 18 = 48x – 41
48x – 24y – 23 = 0
Question 17. Find the equation of the tangent to the curve x2 + 3y − 3 = 0, which is parallel to the line y= 4x − 5.
Solution:
Suppose (a, b) be the required point.
We can find the slope of the given line by differentiating the equation w.r.t x,
So, slope of the line = 4
Since (a, b) lies on the curve, we get a2 + 3b − 3 = 0 . . . . (1)
Now,
2x + 3dy/dx = 0
dy/dx = -2x/3
Slope of tangent, m= 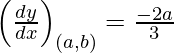
Given that tangent is parallel to the line, So we get,
Slope of tangent, m = slope of the given line
=> -2a/3 = 4
=> a = -6
From (1), we get
=> 36 + 3b – 3 = 0
=> 3b = – 33
=> b = – 11
(a, b) = (-6, -11)
The equation of tangent is,
y – y1 = m (x – x1)
y + 11 = 4 (x + 6)
y + 11 = 4x + 24
4x – y + 13 = 0
Question 18. Prove that 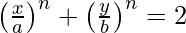 touches the straight line
touches the straight line 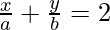 for all n ∈ N, at the point (a, b) ?
for all n ∈ N, at the point (a, b) ?
Solution:
We have,
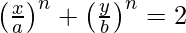
On differentiating both sides, we get
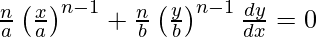
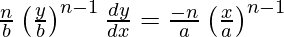
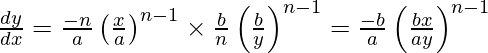
Slope of tangent = 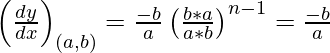
The equation of tangent is,
y – b = -b/a (x – a)
ya – ab = – xb + ab
xb + ya = 2ab
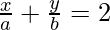
So, the given line touches the given curve at the given point.
Hence proved.
Question 19. Find the equation of the tangent to the curve x = sin 3t, y = cos 2t at t = π/4.
Solution:
We have,
x = sin 3t, y = cos 2t
dx/dt = 3 cos3t and dy/dt = -2sin2t
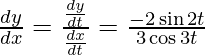
Slope of tangent, m= 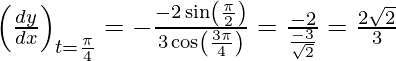
x1 = sin 3π/4 = 1/√2 and y1 = cos π/2 = 0
So, (x1, y1) = (1/√2, 0)
The equation of tangent is,
y – y1 = m (x – x1)
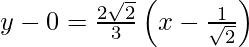
3y = 2√2 x – 2
2√2 x – 3y – 2 = 0
Question 20. At what points will be tangents to the curve y = 2x3 − 15x2 + 36x − 21 be parallel to x-axis? Also, find the equations of the tangents to the curve at these points?
Solution:
We have,
y = 2x3 − 15x2 + 36x − 21
The slope of x – axis is 0.
Let (a, b) be the required point.
Since (a, b) lies on the curve, we get
b = 2a3 − 15a2 + 36a − 21 . . . . (1)
Also, we have
dy/dx = 6 x2 – 30x + 36
Slope of tangent at (a, b) = 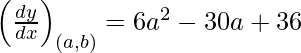
Given that the slope of the tangent = slope of the x-axis, we have
=> 6a2 – 30a + 36 = 0
=> a2 – 5a + 6 = 0
=> (a – 2) (a – 3) = 0
=> a = 2 or a= 3
=> b = 7 or 6
When a = 2 and b = 7, the equation is,
y – y1 = m (x – x1)
y – 7 = 0 (x – 2)
y = 7
When a = 3 and b = 6, the equation is,
y – y1 = m (x – x1)
y – 6 = 0 (x – 3)
y = 6
Question 21. Find the equation of the tangents to the curve 3x2 – y2 = 8, which passes through the point (4/3, 0).
Solution:
We have,
3x2 – y2 = 8 . . . . (1)
On differentiating both sides w.r.t x, we get
6x – 2y dy/dx = 0
2y dy/dx = 6x
dy/dx = 6x/2y
dy/dx = 3x/y
Let tangent at (h, k) pass through (4/3, 0). Since, (h, k) lies on (1), we get
3 h2 – k2 = 8 . . . (ii)
Slope of tangent at (h, k) = 3h/k
The equation of tangent at (h, k) is given by,
y – k = 3h/k (x – h)
Also,
=> 0 – k = (3h/k) (4/3 – h)
=> -k = 4h/k – 3h2/k
=> – k2 = 4h – 3h2
=> 8 – 3 h2 = 4h – 3 h2
=> 8 = 4h
=> h = 2
Also we get,
=> 12 – k2 = 8
=> k2 = 4
=> k = ±2
So, the points on curve (i) at which tangents pass through (4/3, 0) are (2, ±2).
When h = 2 and k = 2, the equation is,
y – 2 = (6/2) (x – 2)
3x – y – 4 = 0
When h = 2 and k = –2, the equation is,
y + 2 = (6/-2) (x – 2)
3x + y – 4 = 0
Like Article
Suggest improvement
Share your thoughts in the comments
Please Login to comment...