Question 1. Discuss the applicability of Rolle’s Theorem for the following functions on the indicated intervals:
(i) f(x) = 3 + (x – 2)2/3 on [1, 3]
Solution:
Rolle’s theorem states that if a function f is continuous on the closed interval [a, b] and
differentiable on the open interval (a, b) such that f(a) = f(b), then f′(x) = 0 for some x with a ≤ x ≤ b.
We have, f'(x) = 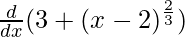
⇒ f'(x) = 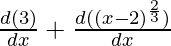
⇒ f'(x) = 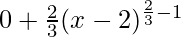
⇒ f'(x) = 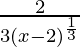
To analyse differentiability at x = 2:
⇒ f'(2) = ![Rendered by QuickLaTeX.com [\frac{2}{3(2-2)}]^{\frac{1}{3}}](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-b9cfa97827fe14c82aa92d4575f37cd0_l3.png)
= 2 / 0 ≠ 0
Since f'(2) ≠ 0, f(x) is not differentiable in the interval [1, 3].
Hence, the Rolle’s Theorem is not applicable for the given function f(x) in interval [1, 3].
(ii) f(x) = [x] for -1 ≤ x ≤ 1, where [x] denotes the greatest integer not exceeding x
Solution:
Rolle’s theorem requires a function to be continuous on the closed interval [a, b].
The continuity of f(x) needs to be analyzed at x = 1:
(RHL at x = 1) = limx⇢(1+h)[x]
= limh⇢0[1 + h]
= 1 ….. (1)
(LHL at x = 1) = limx⇢(1-h)[x]
= limh⇢0[1 – h]
= 0 …… (2)
Since f(x) is not continuous at x = 1 or the interval [-1, 1].
Hence, the Rolle’s Theorem is not applicable for the given function f(x) in interval [-1, 1].
(iii) f(x) = sin(1/x) for -1 ≤ x ≤ 1
Solution:
Rolle’s theorem requires a function to be continuous on the closed interval [a, b].
The continuity of f(x) needs to be analyzed at x = 0:
(RHL at x = 0) = limx⇢(0+h)sin(1/x)
= limh⇢0sin(1/h)
= k …..(1)
(LHL at x = 0) = limx⇢(0-h)sin(1/x)
= limh⇢0sin(1/0-h)
= limh⇢0sin(-1/h)
= -limh⇢0sin(1/h)
= −k ….(2)
Since f(x) is not continuous at x = 1 or the interval [-1,1].
Hence, the Rolle’s Theorem is not applicable for the given function f(x) in interval [-1, 1].
(iv) f(x) = 2x2 – 5x + 3 on [1, 3]
Solution:
Clearly f(x) being a polynomial function shall be continuous on the interval.
We need to verify whether f(a) = f(b) for the applicability of theorem.
Here, f(1) = 2(1)2 – 5(1) + 3
⇒ f(1) = 2 – 5 + 3
⇒ f(1) = 0 …… (1)
Now, f(3) = 2(3)2 – 5(3) + 3
⇒ f(3) = 2(9) – 15 + 3
⇒ f(3) = 18 – 12
⇒ f(3) = 6 …… (2)
From eq(1) and (2), we can say that, f(1) ≠ f(3).
We observe that f(a) ≠ f(b)
Hence, the Rolle’s Theorem is not applicable for the given function f(x) in interval [1, 3].
(v) f (x) = x2/3 on [-1, 1]
Solution:
Rolle’s theorem states that if a function f is continuous on the closed interval [a, b] and
differentiable on the open interval (a, b) such that f(a) = f(b), then f′(x) = 0 for some x with a ≤ x ≤ b.
f'(x) = 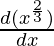
⇒ f'(x) = 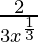
Clearly f'(x) is undefined at x = 0.
Hence, the Rolle’s Theorem is not applicable for the given function f(x) in interval [-1, 1].
(vi) 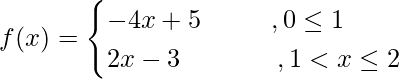
Solution:
Rolle’s theorem requires a function to be continuous on the closed interval [a, b].
The continuity of f(x) needs to be analyzed at x = 1:
(LHL at x = 1) = lim(x->1-h) (-4x + 5)
= lim(h->0) [-4(1 – h) + 5]
= -4 + 5
= 1
(RHL at x = 1) = lim(x->1+h) (2x – 3)
= lim(h->0) [2(1 + h) – 3]
= 2(0) – 3
= -1
We observe that LHL ≠ RHL.
Clearly f(x) is not continuous at x = 1.
Hence, the Rolle’s Theorem is not applicable for the f(x) function in interval [-1, 1].
Question 2. Verify the Rolle’s Theorem for each of the following functions on the indicated intervals:
(i) f (x) = x2 – 8x + 12 on [2, 6]
Solution:
Given function is f (x) = x2 – 8x + 12 on [2, 6].
Since, given function f is a polynomial it is continuous and differentiable everywhere i.e., on R.
We only need to check whether f(a) = f(b) or not.
Thus, f(2) = 22 – 8(2) + 12
⇒ f(2) = 4 – 16 + 12
⇒ f(2) = 0
Now, f(6) = 62 – 8(6) + 12
⇒ f(6) = 36 – 48 + 12
⇒ f(6) = 0
Since f(2) = f(6), Rolle’s theorem is applicable for function f(x) on [2, 6].
f(x) = x2 – 8x + 12
f'(x) = 2x – 8
Then f'(c) = 0
2c – 8 = 0
c = 4 ∈ (2, 6)
Hence, the Rolle’s theorem is verified
(ii) f(x) = x2 – 4x + 3 on [1, 3]
Solution:
Given function is f (x) = x2 – 4x + 3 on [1, 3]
Since, given function f is a polynomial it is continuous and differentiable everywhere i.e., on R.
We only need to check whether f(a) = f(b) or not.
So f (1) = 12 – 4(1) + 3
⇒ f (1) = 1 – 4 + 3
⇒ f (1) = 0
Now, f (3) = 32 – 4(3) + 3
⇒ f (3) = 9 – 12 + 3
⇒ f (3) = 0
∴ f (1) = f(3), Rolle’s theorem applicable for function ‘f’ on [1, 3].
⇒ f’(x) = 2x – 4
We have f’(c) = 0, c ϵ (1, 3), from the definition of Rolle’s Theorem.
⇒ f’(c) = 0
⇒ 2c – 4 = 0
⇒ 2c = 4
⇒ c = 4/2
⇒ c = 2 ∈ (1, 3)
Hence, Rolle’s Theorem is verified.
(iii) f (x) = (x – 1) (x – 2)2 on [1, 2]
Solution:
Given function is f (x) = (x – 1) (x – 2)2 on [1, 2]
Since, given function f is a polynomial it is continuous and differentiable everywhere that is on R.
We only need to check whether f(a) = f(b) or not.
So f (1) = (1 – 1) (1 – 2)2
⇒ f (1) = 0(1)2
⇒ f (1) = 0
Now, f (2) = (2 – 1)(2 – 2)2
⇒ f (2) = 02
⇒ f (2) = 0
Since f (1) = f (2), Rolle’s Theorem applicable for function f(x) on [1, 2].
f(x) = (x – 1)(x – 2)2
f'(x) = (x – 1) × 2(x – 2) + (x – 2)2
f'(x) = (x – 2) (3x – 4)
Then f'(c) = 0
(c – 2)(3c – 4) = 0
c = 2
or
c = 4/3 ∈ (1, 2)
Hence, Rolle’s Theorem is verified.
(iv) f (x) = x (x – 1)2 on [0, 1]
Solution:
Given function is f (x) = x(x – 1)2 on [0, 1]
Since, given function f is a polynomial it is continuous and differentiable everywhere that is, on R.
We only need to check whether f(a) = f(b) or not.
So f (0) = 0 (0 – 1)2
⇒ f (0) = 0
Now f (1) = 1 (1 – 1)2
⇒ f (1) = 02
⇒ f (1) = 0
Since f (0) = f (1), Rolle’s theorem applicable for function f(x) on [0, 1].
f (x) = x (x – 1)2
f'(x) = (x – 1)2+ x × 2(x – 1)
= (x – 1)(x – 1 + 2x)
= (x – 1)(3x – 1)
Then f'(c) = 0
(c – 1)(3c – 1) = 0
c = 1 or 1/3 ∈ (0, 1)
Hence, Rolle’s Theorem is verified.
(v) f (x) = (x2 – 1) (x – 2) on [-1, 2]
Solution:
Given function is f (x) = (x2 – 1) (x – 2) on [– 1, 2]
Since, given function f is a polynomial it is continuous and differentiable everywhere that is on R.
We only need to check whether f(a) = f(b) or not.
So f(–1) = (( – 1)2 – 1)( – 1 – 2)
⇒ f ( – 1) = (1 – 1)( – 3)
⇒ f ( – 1) = (0)( – 3)
⇒ f ( – 1) = 0
Now, f (2) = (22 – 1)(2 – 2)
⇒ f (2) = (4 – 1)(0)
⇒ f (2) = 0
∴ f (– 1) = f (2), Rolle’s theorem applicable for function f on[ – 1, 2].
⇒ f’(x) = 3x2 – 4x – 1
We have f’(c) = 0 c ∈ (-1, 2), from the definition of Rolle’s Theorem.
Clearly, f'(c) = 0
3c2 – 4c – 1 = 0
c = (2 ±√7)/ 3
c = 1/3(2 + √7) or 1/3(2 – √7) ∈ (-1, 2)
Hence, Rolle’s Theorem is verified.
(vi) f(x) = x(x – 4)2 on [0, 4]
Solution:
Given function is f (x) = x(x – 4)2 on [0, 4]
Since, given function f is a polynomial it is continuous and differentiable everywhere i.e., on R.
We only need to check whether f(a) = f(b) or not.
So f (0) = 0(0 – 4)2
⇒ f (0) = 0
Now, f (4) = 4(4 – 4)2
⇒ f (4) = 4(0)2
⇒ f (4) = 0
Since f (0) = f (4), Rolle’s theorem applicable for function f(x) on [0, 4].
f(x) = x(x – 4)2
f'(x) = x × 2(x – 4) + (x – 4)2
= 2x2 – 8x + x2 + 16 – 8x
= 2x2 – 16x + 16
Then
f'(c) = 2c2 – 16c + 16
= (c – 4)(3c – 4)
c = 4 or 4/3 ∈ (0, 4)
Hence, Rolle’s Theorem is verified.
(vii) f (x) = x(x – 2)2 on [0, 2]
Solution:
Given function is f (x) = x(x – 2)2 on [0, 2].
Since, given function f is a polynomial it is continuous and differentiable everywhere that is on R.
We only need to check whether f(a) = f(b) or not.
So f (0) = 0(0 – 2)2
⇒ f (0) = 0
Now, f (2) = 2(2 – 2)2
⇒ f (2) = 2(0)2
⇒ f (2) = 0
f (0) = f(2), Rolle’s theorem applicable for function f on [0,2].
c = 12/6 or 4/6
c = 2 or 2/3
So, c = 2/3 since c ∈ (0, 2)
Hence, Rolle’s Theorem is verified.
(viii) f (x) = x2 + 5x + 6 on [-3, -2]
Solution:
Given function is f (x) = x2 + 5x + 6 on [– 3, – 2].
Since, given function f is a polynomial it is continuous and differentiable everywhere i.e., on R.
We only need to check whether f(a) = f(b) or not.
So f(–3) = (–3)2 + 5(–3) + 6
⇒ f(–3) = 9 – 15 + 6
⇒ f(–3) = 0
Now, f(–2) = (–2)2 + 5(–2) + 6
⇒ f(–2) = 4 – 10 + 6
⇒ f(–2) = 0
Since f(–3) = f(–2), Rolle’s theorem applicable for function f(x) on [–3, –2].
f(x) = x2 + 5x + 6
f'(x) = 2x + 5
Then
f(c) = 0
2c + 5 = 0
c = -5/2 ∈ (-3, -2)
Hence, Rolle’s Theorem is verified.
Question 3. Verify the Rolle’s Theorem for each of the following functions on the indicated intervals:
(i) f(x) = cos2(x – π/4) on [0, π/2]
Solution:
Clearly the cosine function is continuous and differentiable everywhere.
Hence, the given function f(x) is continuous in [0, π/2] and differentiable in [0, π/2]
So,
f(0) = cos2(0 – π/4) = 0
f(π/2) = cos2(π/2 – π/4) = 0
Since f(0) = f(π/2), Rolle’s theorem applicable for function f(x) on [0, π/2].
Now, f'(x) = 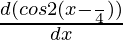
= -2sin(2x – π/2)
If f'(c) = 0
⇒ -2sin(2c – π/2) = 0
⇒ c = π/4 ∈ [0, π/2]
Clearly c belongs to the given interval.
Hence, Rolle’s Theorem is verified.
(ii) f(x) = sin 2x on [0, π/2]
Solution:
Since sin 2x is everywhere continuous and differentiable.
So, sin2x is continuous on (0, π/2) and differentiable on (0, π/2).
f(0) = sin 0 = 0
f(π/2) = sin π/2 = 0
f(π/2) = f(0) = 0
Thus, f(x) satisfies all the conditions of Rolle’s theorem.
Now, we have to show that there exists c in (0, π/2) such that f'(c) = 0.
We have, f'(x) = 0
⇒ cos2x = 0
⇒ x = π/4
So, f'(c) = 2cos2c
2cos2c = 0
Thus, c = π/4 in (0, π/2).
Hence, Rolle’s theorem is verified.
(iii) f(x) = cos2x on [-π/4, π/4]
Solution:
Since cos 2x is everywhere continuous and differentiable.
So, cos2x is continuous on [-π/4, π/4] and differentiable on [-π/4, π/4].
cos(-π/4) = cos2(-π/4) = cos(-π/2) = 0
cos(π/4) = cos2(π/4) = cos(π/2) = 0
Also, cos(-π/4) = cos(π/4)
Thus, f(x) satisfies all the conditions of Rolle’s theorem.
Now, we have to show that there exists c in (0, π/2) such that f'(c) = 0.
We have f'(x) = 0
⇒ sin2c = 0
⇒ 2c = 0
So, c = 0 as c ∈ (-π/4, π/4)
Hence, Rolle’s Theorem is verified for the given function f(x).
(iv) ex sin x on [0, π]
Solution:
The given function is a composition of exponential and trigonometric functions. Hence it is differential and continuous everywhere.
So, the given function f(x) is continuous on [0, π] and differentiable on (0, π).
f(0) = e0 sin 0 = 0
f(π) = eπ sin π = 0
f(0) = f(π)
Now, we have to show that there exists c in (0, π) such that f'(c) = 0.
So f'(x) = ex (sin x + cos x)
⇒ ex (sin x + cos x) = 0
⇒ sin x + cos x = 0
Dividing both sides by cos x, we have
tan x = -1
⇒ x = π – π/4 = 3π/4
Since c = 3π/4 in (0, π) such that f'(c) = 0.
Hence, Rolle’s theorem is verified for the given function f(x).
(v) f(x) = ex cos x on [−π/2, π/2]
Solution:
The given function is a composition of exponential and trigonometric functions. Hence it is differential and continuous everywhere.
So, the given function f(x) is continuous on [-π/2, π/2] and differentiable on (-π/2, π/2).
f(−π/2) = eπ/2 cos(−π/2) = 0
f(π/2) = eπ/2 cos(π/2) = 0
f(−π/2) = f(π/2)
Now, we have to show that there exists c in (-π/2, π/2) such that f'(c) = 0.
f'(x) = ex (cos x – sin x)
⇒ ex (cos x – sin x) = 0
⇒ sin x – cos x = 0
Dividing both sides by cos x, we have
tan x = 1
⇒ x = π/4
Since c = π/4 in (-π/2, π/2) such that f’(c) = 0.
Hence, Rolle’s theorem is verified for the given function f(x).
(vi) f (x) = cos 2x on [0, π]
Solution:
Since cos 2x is everywhere continuous and differentiable.
So, cos2x is continuous on [0, π] and differentiable on (0, π).
f(0) = cos(0) = 1
f(π) = cos(2π) = 1
f(0) = f(π)
Thus, f(x) satisfies all the conditions of Rolle’s theorem.
There must be a c belongs to (0, π) such that f’(c) = 0.
⇒ sin 2c = 0
So, 2c = 0 or π
c = 0 or π/2
But, c = π/2 as c ∈ (0, π)
Hence, Rolle’s Theorem is verified for the given function f(x).
(vii) f(x) = sinx/ex on 0 ≤ x ≤ π
Solution:
The given function is a composition of exponential and trigonometric functions.
Hence it is differential and continuous everywhere.
So, sinx/ex is continuous on [0, π] and differentiable on (0, π).
f(0) = sin(0)/e0 = 0
f(π) = sin(π)/eπ = 1
f(0) = f(π)
Now, we have to show that there exists c in (0, π/2) such that f'(c) = 0.
f'(x) = ex (cos x – sin x)
⇒ ex (cos x – sin x) = 0
⇒ sin x – cos x = 0
⇒ tan x = 1
⇒ x = π/4
Since c = π/4 in (-π/4, π/4) such that f’(c) = 0.
Hence, Rolle’s theorem is verified for the given function f(x).
(viii) f(x) = sin 3x on [0, π]
Solution:
Given function is f (x) = sin3x on [0, π]
Since sine function is continuous and differentiable on R.
We need to check whether f(a) = f(b) or not.
So f (0) = sin 3(0)
⇒ f (0) = sin0
⇒ f (0) = 0
Now, f (π) = sin 3π
⇒ f (π) = sin(3 π)
⇒ f (π) = 0
We have f (0) = f (π), so there exist a c belongs to (0, π) such that f’(c) = 0.
⇒ 3cos(3x) = 0
⇒ cos 3x = 0
⇒ 3x = π / 2
⇒ x = π / 6 ∈ [0, π]
Hence, Rolle’s theorem is verified for the given function f(x).
(ix) f(x) = 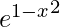 on [−1, 1]
on [−1, 1]
Solution:
We know that the exponential function is continuous and differentiable everywhere.
So, 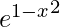 is continuous on [-1, 1] and differentiable on (-1, 1).
is continuous on [-1, 1] and differentiable on (-1, 1).
f(-1) = e1-1 = 1
f(1) = e1-1 = 1
Also, f(-1) = f(1) = 1
Thus, Rolle’s theorem is applicable. So there must exist c ∈ [−1, 1] such that f'(c) = 0.
f'(x) = ![Rendered by QuickLaTeX.com -2x [e^{1 - x^2}]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-13d83976bb86a3a63ef5efea06798ac8_l3.png)
⇒ -2x e^{1 – x^2} = 0
⇒ x = 0 ∈ [−1, 1]
Hence, Rolle’s theorem is verified.
(x) f (x) = log (x2 + 2) – log 3 on [-1, 1]
Solution:
Clearly the logarithmic function is continuous and differentiable in its own domain.
We need to verify whether f(a) = f(b) or not.
So f (– 1) = log((– 1)2 + 2) – log 3
⇒ f (– 1) = log (1 + 2) – log 3
⇒ f (– 1) = log 3 – log 3
⇒ f ( – 1) = 0
Now, f (1) = log (12 + 2) – log 3
⇒ f (1) = log (1 + 2) – log 3
⇒ f (1) = log 3 – log 3
⇒ f (1) = 0
We have got f (– 1) = f (1).
So, there exists a c such that c ϵ (– 1, 1) such that f’(c) = 0.
Now, f'(x) = 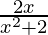
f'(c) = 0
⇒ c = 0 ϵ (– 1, 1)
Hence, Rolle’s theorem is verified.
(xi) f(x) = sin x + cos x on [0, π/2]
Solution:
Since sin and cos functions are continuous and differentiable everywhere,
f(x) is continuous on [0, π/2] and differentiable on (0, π/2).
So, f(0) = sin 0 + cos 0 = 1
f(π/2) = sin π/2 + cos π/2 = 1
Also, f(0) = f(π/2) = 1.
Hence, Rolle’s theorem is applicable. So there must exist c ∈ [−1, 1] such that f'(c) = 0.
Now, f'(x) = cos x – sin x
⇒ cos x – sin x = 0
⇒ tan x = 1
⇒ x = π/4
Thus, c = π/4 on (0, π/2).
Hence, Rolle’s theorem is verified for the given function f(x).
(xii) f (x) = 2 sin x + sin 2x on [0, π]
Solution:
Since sin function continuous and differentiable over R, f(x) is continuous on [0, π] and differentiable on (0, π).
We need to verify whether f(a) = f(b) or not.
So f (0) = 2sin(0) + sin2(0)
⇒ f (0) = 2(0) + 0
⇒ f (0) = 0
Now, f (π) = 2sin(π) + sin2(π)
⇒ f (π) = 2(0) + 0
⇒ f (π) = 0
We have f (0) = f (π), so there exist a c belongs to (0, π) such that f’(c) = 0.
f'(x) = 2cos x + cos 2x
Now, f'(c) = 0
⇒ 2cos x + cos 2x = 0
⇒ (2cos c – 1) (cos c + 1) = 0
⇒ tan c = 1
⇒ c = π/3 in (0, π)
Hence, Rolle’s theorem is verified for the given function f(x).
(xiii) f(x) = ![Rendered by QuickLaTeX.com \frac{x}{2} - \sin[\frac{\pi x}{6}]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-6ca6d37d4bb2b8131b8b7b24f8513044_l3.png) on [-1, 0]
on [-1, 0]
Solution:
Since sin function is continuous and differentiable over R, f(x) is continuous on [-1, 0] and differentiable on (-1, 0).
f(-1) = ![Rendered by QuickLaTeX.com \frac{-1}{2} - \sin[\frac{\pi (-1)}{6}]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-062a475861b19ab68016bddbc864df21_l3.png) = 0
= 0
f(0) = 0 – sin 0 = 0
Also f(-1) = f(0) = 0
Hence Rolle’s theorem is applicable so there exist a c belongs to (0, π) such that f’(c) = 0.
f'(x) = ![Rendered by QuickLaTeX.com \frac{1}{2} - \frac{\pi}{6}\cos[\frac{\pi x}{6}]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-e215a918dec976bec3cfc2ea03d3d5df_l3.png)
Now, f'(c) = 0
⇒ ![Rendered by QuickLaTeX.com \frac{1}{2} - \frac{\pi}{6}\cos[\frac{\pi c}{6}] = 0](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-dc3d64edb18767c5347e19640a33bb49_l3.png)
⇒ 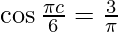
⇒ c = ![Rendered by QuickLaTeX.com (\frac{- 6}{\pi}) \cos^{- 1} [\frac{3}{\pi}]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-c8d91d3bbf1722ee933290b7b056ab7c_l3.png)
Thus, c ϵ (-1, 0).
Hence, Rolle’s theorem is verified for the given function f(x).
(xiv) f(x) = 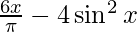 on [0, π/6]
on [0, π/6]
Solution:
Since sin function is continuous and differentiable everywhere, f(x) is continuous on [0, π/6] and differentiable on (0, π/6).
f(0) = 0 – 0 = 0
f(π/6) = 1 – 1 = 0
Also, f(0) = f(π/6) = 0
Hence Rolle’s theorem is applicable so there exist a c belongs to (0, π/6) such that f’(c) = 0.
We have, f'(x) = 6/π – 8sinxcosx
f'(x) = 6/π – 4sin2x
f'(c) = 0
6/π – 4sin2c = 0
4sin2c = 6/π
sin2c = 3/2π
2c = sin-1(21/44)
c = 1/2 sin-1(21/44)
c ∈ (-1/2, 1/2)
c ∈ (0, 11/21)
c ∈ (0, π/6)
Hence, Rolle’s theorem is verified for the given function f(x).
(xv) f(x) = 4sin x on [0, π]
Solution:
Since sin and exponential functions are continuous and differentiable everywhere, f(x) is continuous on [0, π] and differentiable on (0, π).
f(0) = 4sin 0 = 1
f(π) = 4sin π = 1
Also, f(0) = f(π) = 1.
Hence Rolle’s theorem is applicable so there exist a c belongs to (0, π) such that f’(c) = 0.
We have, f'(x) = 4sin x cos x log 4
So, f’(c) = 0
4sin c cos c log 4 = 0
4sin c cos c = 0
cos c = 0
c = π/2 ∈ (0, π)
Hence, Rolle’s theorem is verified for the given function f(x).
(xvi) f (x) = x2 – 5x + 4 on [1, 4]
Solution:
Since, given function f is a polynomial it is continuous and differentiable everywhere i.e., on R.
We need to verify whether f(a) = f(b) or not.
So f (1) = 12 – 5(1) + 4
⇒ f (1) = 1 – 5 + 4
⇒ f (1) = 0
Now, f (4) = 42 – 5(4) + 4
⇒ f (4) = 16 – 20 + 4
⇒ f (4) = 0
We have f (1) = f (4). So, there exists a c ∈ (1, 4) such that f’(c) = 0.
f'(x) = 2x – 5
Now, f'(c) = 2c – 5 = 0
Thus, c = 5 / 2 ∈ (1, 4).
Hence, Rolle’s theorem is verified for the given function f(x).
(xvii) f(x) = sin4 x + cos4 x on (0, π/2)
Solution:
Since sin and cos functions are continuous and differentiable everywhere, f(x) is continuous on [0, π/2] and differentiable on (0, π/2).
So,
f(0) = sin4(0) + cos4(0) = 1
f(π/2) = sin4(π/2) + cos4(π/2) = 1
f(0) = f(π/2)
Hence Rolle’s theorem is applicable so there exist a c belongs to (0, π/2) such that f’(c) = 0.
⇒ f'(x) = 4sin3 x cos x – 4cos3 x sin x
so, f'(c) = 4sin3 x cos x – 4cos3 x sin x = 0
4sin3 c cos c – 4cos3 c sin c = 0
-sin4c = 0
4x = 0 or 4x = π
x = 0, or π/4 ∈ (0, π/2)
Hence, Rolle’s theorem is verified.
(xviii) f(x) = sin x – sin 2x on [0, π]
Solution:
Given function is f (x) = sin x – sin2x on [0, π]
We know that sine function is continuous and differentiable over R.
Now we have to check the values of the function ‘f’ at the extremes.
⇒ f (0) = sin (0) – sin 2(0)
⇒ f (0) = 0 – sin (0)
⇒ f (0) = 0
⇒ f (π) = sin(π) – sin2(π)
⇒ f (π) = 0 – sin(2π)
⇒ f (π) = 0
We have f (0) = f (π). So, there exists a c ∈ (0, π) such that f’(c) = 0.
f'(x) = cos x – 2cos 2x
so, f'(c) = 0
f'(c) = cos c – 2cos 2c = 0
cos c – (2cos2c + 1) = 0
2cos2 c – cosc – 1 = 0
(cos c – 1)(2cos c + 1) = 0
cos c = 1, -1/2
c = cos(π/2), cos(2π/3)
So, c = π/2, 2π/3 ∈ (0, π)
Hence, Rolle’s theorem is verified.
Question 4. Using Rolle’s Theorem, find points on the curve y = 16 – x2, x ∈ [-1, 1], where the tangent is parallel to the x-axis.
Solution:
Given: y = 16 – x2, x ϵ [– 1, 1]
⇒ y (– 1) = 16 – (– 1)2
⇒ y (– 1) = 16 – 1
⇒ y (– 1) = 15
Now, y (1) = 16 – (1)2
⇒ y (1) = 16 – 1
⇒ y (1) = 15
We have y (– 1) = y (1). So, there exists a c ϵ (– 1, 1) such that f’(c) = 0.
We know that for a curve g, the value of the slope of the tangent at a point r is given by g’(r).
⇒ y’ = –2x
We have y’(c) = 0
⇒ – 2c = 0
⇒ c = 0 ϵ (– 1, 1)
Value of y at x = 1 is
⇒ y = 16 – 02
⇒ y = 16
Hence, the point at which the curve y has a tangent parallel to x – axis (since the slope of x – axis is 0) is (0, 16).
Question 5. At what points on the following curves is the tangent parallel to the x-axis?
(i) y = x2 on [-2, 2]
Solution:
Given: f(x) = x2
f'(x) = 2x
Also, f(-2) = f(2) = 22 = (-2)2 = 4
So, there exists a c ϵ (-2, 2) such that f’(c) = 0.
⇒ 2c = 0
⇒ c = 0
Therefore the required point is (0, 0).
(ii) y = 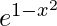 on [−1, 1]
on [−1, 1]
Solution:
Since exponential function is continuous and differentiable everywhere.
Here f(1) = f(-1) = 1
Thus, all the conditions of Rolle’s theorem are satisfied.
Consequently, there exists at least one point c in (-1, 1) for which f'(c) = 0.
⇒ f'(c) = 0
⇒ -2c e^{1 – c^2} = 0
⇒ c = 0
Hence, (0, e) is the required point.
(iii) y = 12 (x + 1) (x − 2) on [−1, 2]
Solution:
Since polynomial function is continuous and differentiable everywhere.
Here f(2) = f(-1) = 0.
Thus, all the conditions of Rolle’s theorem are satisfied.
Consequently, there exists at least one point c in (-1, 2) for which f'(c) = 0.
But f'(c) = 0
⇒ 24c – 12 = 0
⇒ c = 1/2
Hence, (1/2, -27) is the required point.
Question 6. If f: [5, 5] to R is a differentiable function and if f'(x) does not vanish anywhere, prove that f(-5) ≠ f(5).
Solution:
Here f(x) is differentiable on (5,5).
By Mean Value Theorem,
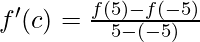
⇒ 10 f'(c) = f(5) – f(-5)
It is also given that f'(x) does not vanish anywhere.
⇒ f'(c) ≠ 0
⇒ 10 f'(c) ≠ 0
⇒ f(5) – f(-5) ≠ 0
⇒ f(5) ≠ f(-5)
Hence Proved
Question 7. Examine if Rolle’s theorem is applicable to any one of the following functions.
(i) f (x) = [x] for x ∈ [5, 9]
(ii) f (x) = [x] for x ∈ [−2, 2]
Can you say something about the converse of Rolle’s Theorem from these functions?
Solution:
Rolle’s theorem states that if a function f is continuous on the closed interval [a, b] and differentiable on the open interval (a, b) such that f(a) = f(b), then f′(x) = 0 for some x with a ≤ x ≤ b.
(i) f(x) = [x] for x ∈ [ 5 , 9 ]
f(x) is not continuous at x = 5 and x = 9. Thus, f (x) is not continuous on [5, 9].
Also , f (5) = [5] = 5 and f (9) = [9] = 9
∴ f (5) ≠ f (9)
The left hand limit of f at x = n is ∞ and the right hand limit of f at x = n is 0.
Since the left and the right hand limits of f at x = n are not equal, f is not differentiable on (5, 9).
Hence, Rolle’s theorem is not applicable on function f(x) for x ∈ [5 , 9].
(ii) f (x) = [x] for x ∈ [-2 , 2]
f(x) is not continuous at x = −2 and x = 2. Thus, f (x) is not continuous on [−2, 2].
Also, f (-2) = [-2] = -2 and f (2) = [2] = 2
∴ f (-2) ≠ f (2)
The left hand limit of f at x = n is ∞ and the right hand limit of f at x = n is ∞.
Since the left and the right hand limits of f at x = n are not equal, thus, f is not differentiable on (−2, 2).
Hence, Rolle’s theorem is not applicable on function f(x) = [x] for x ∈ [ -2, 2].
Share your thoughts in the comments
Please Login to comment...