Class 12 RD Sharma Solutions – Chapter 11 Differentiation – Exercise 11.7 | Set 3
Last Updated :
20 May, 2021
Question 21. If 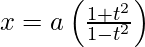 and
and 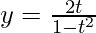 , find
, find 
Solution:
Here,
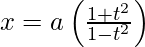
Differentiate it with respect to t using chain rule,
![Rendered by QuickLaTeX.com \frac{dx}{dt}=a\left[\frac{(1+t^2)\frac{d}{dt}(1+t^2)-(1+t^2)\frac{d}{dt}(1-t^2)}{(1-t^2)^2}\right]\\ =a\left[\frac{(1-t^2)(2t)-(1+t^2)(-2t)}{(1-t^2)^2}\right]\\ =a\left[\frac{2t-2t^2+2t+2t^3}{(1-t^2)^2}\right]\\ \frac{dy}{dt}=\frac{4at}{(1-t^2)^2}\ \ \ \ \ ......(1)](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-78c9cca0b22ccef4f6a2805fd8c262e2_l3.png)
And,
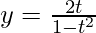
Differentiate it with respect to t using quotient rule,
![Rendered by QuickLaTeX.com \frac{dy}{dt}=a\left[\frac{(1-t^2)\frac{d}{dt}(t)-(t)\frac{d}{dt}(1-t^2)}{(1-t^2)^2}\right]\\ =a\left[\frac{(1-t^2)(1)-(t)(-2t)}{(1-t^2)^2}\right]\\ =a\left[\frac{1-t^2+2t}{(1-t^2)^2}\right]\\ \frac{dy}{dt}=\frac{2(1+t^2)}{(1-t^2)}\ \ \ \ \ ......(2)](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-d6666789cfaf8602c2de3586d7a22c0e_l3.png)
Question 22. Find  , if y = 12(1 – cos t), x = 10(t – sin t),
, if y = 12(1 – cos t), x = 10(t – sin t), 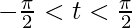
Solution:
It is given that,
y = 12(1 – cos t),
x = 10(t – sin t)
Therefore,
![Rendered by QuickLaTeX.com \frac{dx}{dt}=\frac{d}{dt}[10(t-sin\ t)]\\ =10.\frac{d}{dt}(t-sin\ t)\\ =10(1- cos\ t)](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-a5821a6c533f17ab1db3d21f910ed16b_l3.png)
![Rendered by QuickLaTeX.com \frac{dy}{dt}=\frac{d}{dt}[12(t-cos\ t)]\\ =12.\frac{d}{dt}(1-cos\ t)\\ =12(0- (-sin\ t)\\ =12sin\ t](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-8b8861608e05ce404fb33a4dd4b84306_l3.png)
Therefore,
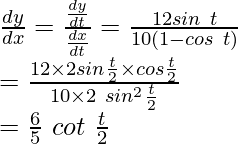
Question 23. If x = a(θ – sin θ) and y = a(1 – cos θ), find  , at θ =
, at θ = 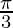
Solution:
Here,
x = a(θ – sin θ)
and
y = a(1 – cos θ)
Then,
![Rendered by QuickLaTeX.com \frac{dx}{dθ}=\frac{d}{dθ}[a(θ-sin\ θ]\\ =a(1-cos\ θ)](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-fb0cb2cf9f14fcd2fee563b88ace822c_l3.png)
![Rendered by QuickLaTeX.com \frac{dy}{dθ}=\frac{d}{dθ}[a(1+cos\ θ]\\ =a(-sin\ θ)](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-c9eae855907909f2b53212d690b56208_l3.png)
Therefore,

Question 24. If x = a sin 2t (1 + cos 2t) and y = b cos 2t (1 – cos 2t), show that at t = 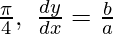
Solution:
Consider the given functions,
x = a sin 2t (1 + cos 2t)
and
y = b cos 2t (1 – cos 2t)
Write again the functions,
x = a sin 2t +  sin 4t
sin 4t
Differentiate the above function with respect to t,
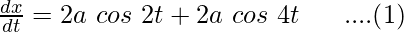
y = b cos 2t (1 – cos 2t)
y = b cos 2t – b cos2 2t
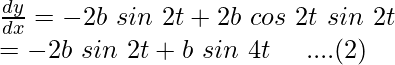
From equation (1) and (2)
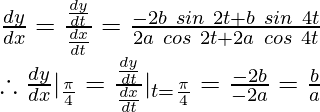
Question 25. If x = cos t (3 – 2cos2t) and y = sin t (3 – 2 sin2t), find the value of  at t =
at t = 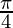
Solution:
Here, the given function:
x = cos t (3 – 2cos2t)
x = cos t – 2cos3t
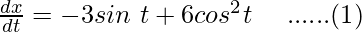
y = sin t (3 – 2 sin2t)
y = 3cos t – 2sin3t

Question 26. If 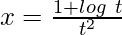 ,
, 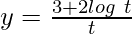 find
find 
Solution:
Here,
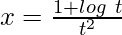
and
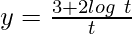
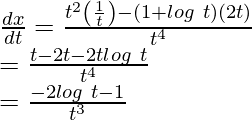
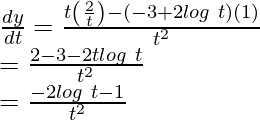
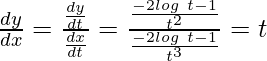
Question 27. If x = 3sin t – sin3t, y = 3cos t – cos3t, find 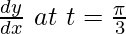
Solution:
x = 3sin t – sin3t
and,
y = 3cos t – cos3t
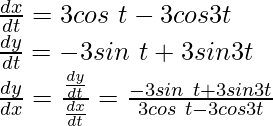
When, 
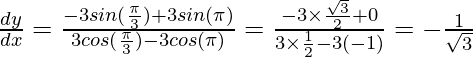
Question 28. If 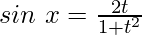 ,
,  find
find 
Solution:
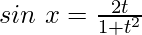
and,
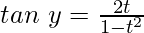
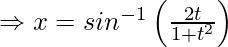
and

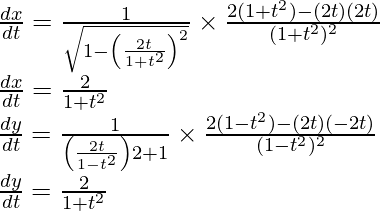
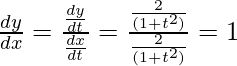
Share your thoughts in the comments
Please Login to comment...