Class 12 RD Sharma Solutions – Chapter 8 Solution of Simultaneous Linear Equations – Exercise 8.2
Last Updated :
13 Jan, 2021
Solve the following systems of homogeneous linear equations by matrix method:
Question 1.
2x – y + z = 0
3x + 2y – z = 0
x + 4y + 3z = 0
Solution:
Given
2x – y + z = 0
3x + 2y – z = 0
X + 4y + 3z = 0
The system can be written as
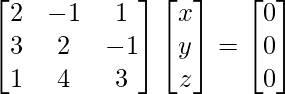
A X = 0
Now, |A| = 2(6 + 4) + 1(9 + 1) + 1(12 – 2)
|A| = 2(10) + 10 + 10
|A| = 40 ≠ 0
Since, |A|≠ 0, hence x = y = z = 0 is the only solution of this homogeneous equation.
Question 2.
2x – y + 2z = 0
5x + 3y – z = 0
X + 5y – 5z = 0
Solution:
Given 2x – y + 2z = 0
5x + 3y – z = 0
X + 5y – 5z = 0
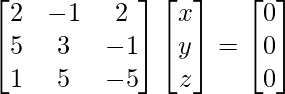
A X = 0
Now, |A| = 2(– 15 + 5) + 1(– 25 + 1) + 2(25 – 3)
|A| = – 20 – 24 + 44
|A| = 0
Thus, the system has infinite solutions
Let z = k
2x – y = – 2k
5x + 3y = k
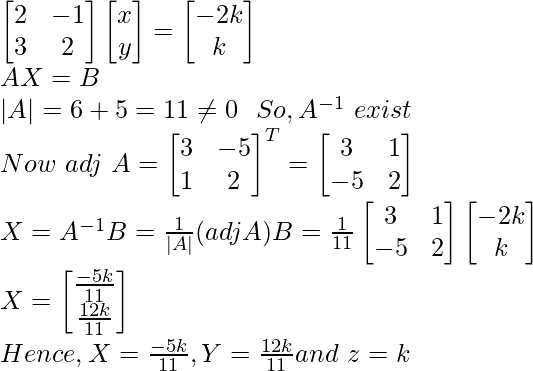
Question 3.
3x – y + 2z = 0
4x + 3y + 3z = 0
5x + 7y + 4z = 0
Solution:
Given:
3x – y + 2z = 0
4x + 3y + 3z = 0
5x + 7y + 4z = 0
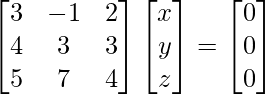
A X = 0
Now, |A| = 3(12 – 21) + 1(16 – 15) + 2(28 – 15)
|A| = – 27 + 1 + 26
|A| = 0
Hence, the system has infinite solutions
Let z = k
3x – y = – 2k
4x + 3y = – 3k
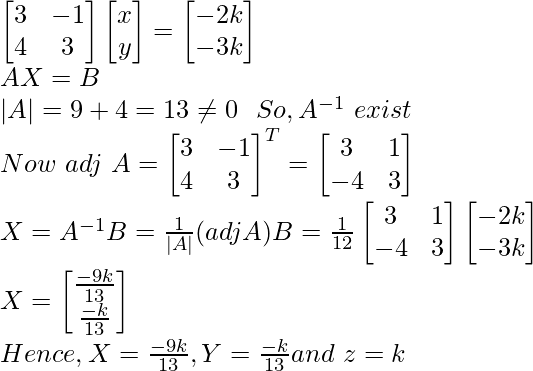
Question 4.
x + y – 6z = 0
x – y + 2z = 0
– 3x + y + 2z = 0
Solution:
Given:
x + y – 6z = 0
x – y + 2z = 0
– 3x + y + 2z = 0
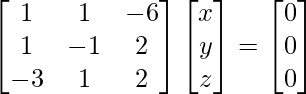
A X = 0
Now, |A| = 1(– 2 – 2) – 1(2 + 6) – 6(1 – 3)
|A| = – 4 – 8 + 12
|A| = 0
Hence, the system has infinite solutions
Let z = k
x + y = 6k
x – y = – 2k
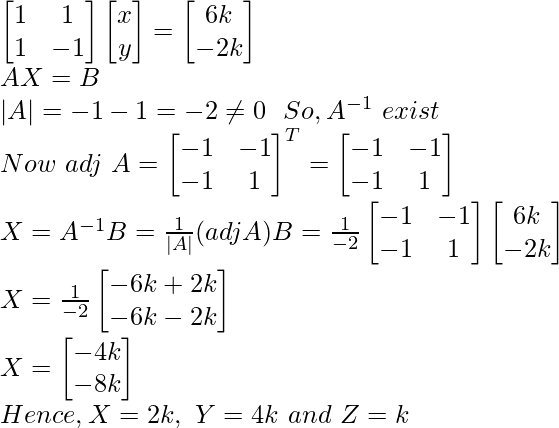
Question 5. Solve the system of homogeneous linear equations by matrix method:
x + y + z = 0
x – y – 5z = 0
x + 2y + 4z = 0
Solution:
Given:
x + y + z = 0
x – y – 5z = 0
x + 2y + 4z = 0
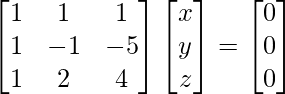
A X = 0
Now, |A| = 1(6) – 1(9) + 1(3)
|A| = 9 – 9
|A| = 0
Hence, the system has infinite solutions
Let z = k
x + y = –k
x – y = 5k
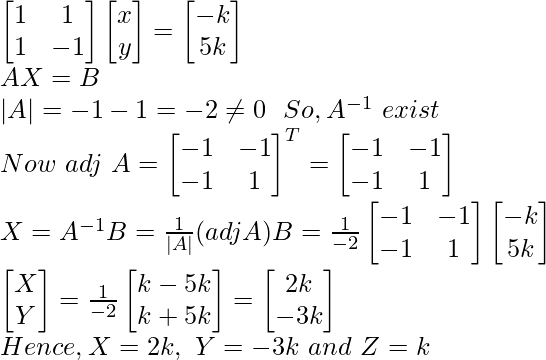
Question 6. Solve the system of homogeneous linear equations by matrix method:
x + y – z = 0
x – 2y + z = 0
3x + 6y –5z = 0
Solution:
Given:
x + y – z = 0
x – 2y + z = 0
3x + 6y –5z = 0
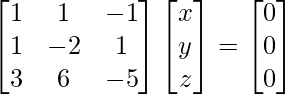
A X = 0
Now, |A| = 1(4) – 1(–8) – 1(12)
|A| = 4 + 8 – 12
|A| = 0
Hence, the system has infinite solutions
Let z = k
x + y = –k
x – 2y = –k
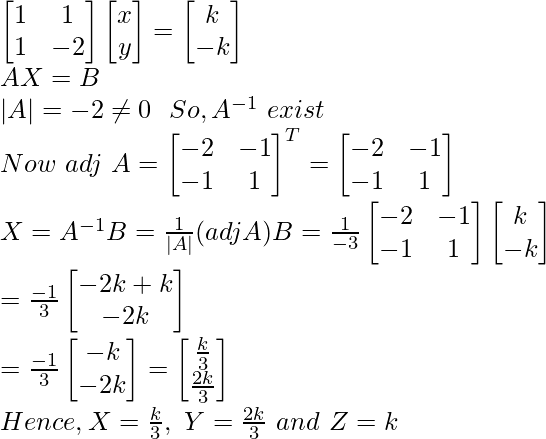
Question 7. Solve the system of homogeneous linear equations by matrix method:
3x + y – 2z = 0
x + y + z = 0
x – 2y + z =0
Solution:
Given:
3x + y – 2z = 0
x + y + z = 0
x – 2y + z =0
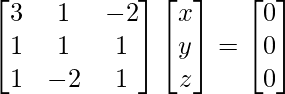
A X = 0
Now, |A| = 3(3) – 1(0) – 2(–3)
|A| = 9 – 0 + 6
|A| = 15 ≠ 0,
Hence, the given system has only trivial solutions given by x = y = z = 0.
Question 8. Solve the system of homogeneous linear equations by matrix method:
2x + 3y – z =0
x – y – 2z = 0
3x + y + 3z = 0
Solution:
Given:
2x + 3y – z =0
x – y – 2z = 0
3x + y + 3z = 0
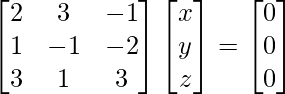
A X = 0
Now, |A| = 2(–3 + 2) – 3(3 + 6) – 1(4)
|A| = –2 – 27 – 4
|A| = –33 ≠ 0,
Hence, the given system has only trivial solutions given by x = y = z = 0.
Share your thoughts in the comments
Please Login to comment...