Class 12 RD Sharma Solutions – Chapter 6 Determinants – Exercise 6.5
Last Updated :
16 Dec, 2021
Question 1. Solve each of the following system of homogeneous linear equations:
x + y – 2z = 0
2x + y – 3z =0
5x + 4y – 9z = 0
Solution:
Given:
x + y – 2z = 0
2x + y – 3z =0
5x + 4y – 9z = 0
This system of equations can be expressed in the form of a matrix AX = B
Now find the determinant,
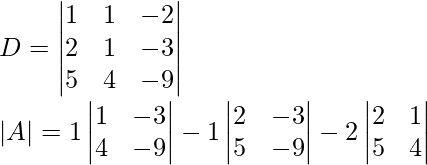
= 1(1 × (-9) – 4 × (-3)) – 1(2 × (-9) – 5 × (-3)) – 2(4 × 2 – 5 × 1)
= 1(-9 + 12) – 1(-18 + 15) – 2(8 – 5)
= 1 × 3 – 1 × (-3) – 2 × 3
= 3 + 3 – 6
= 0
So, D = 0, that means this system of equations has infinite solution.
Now,
Let z = k
⇒ x + y = 2k
And 2x + y = 3k
Now using the Cramer’s rule
x = 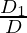
x = 
x = 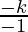
x = k
Similarly,
y = 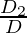
y = 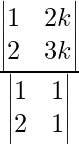
y = 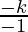
y = k
Therefore,
x = y = z = k.
Question 2. Solve each of the following system of homogeneous linear equations:
2x + 3y + 4z = 0
x + y + z = 0
2x + 5y – 2z = 0
Solution:
2x + 3y + 4z = 0
x + y + z = 0
2x + 5y – 2z = 0
This system of equations can be expressed in the form of a matrix AX = B
Find the determinant
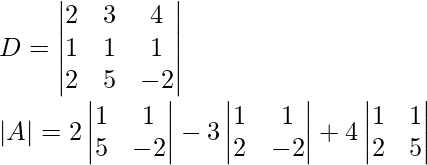
= 2(1 × (-2) – 1 × 5) – 3(1 × (-2) – 2 × 1) + 4(1 × 5 – 2 × 1)
= 2(-2 – 5) – 3(-2 – 2) + 4(5 – 2)
= 2 × (-7) – 3 × (-4) + 4 × 3
= -14 + 12 + 12
= -10
Hence, D ≠ 0, so the system of equation has trivial solution.
Therefore, the system of equation has only solution as x = y = z = 0.
Question 3. Solve each of the following system of homogeneous linear equations:
3x + y + z = 0
x – 4y + 3z = 0
2x +5y – 2z = 0
Solution:
Given:
3x + y + z = 0
x – 4y + 3z = 0
2x +5y – 2z = 0
This system of equations can be expressed in the form of a matrix AX = B
Find the determinant
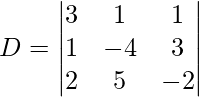
= 3(8 – 15) – 1(-2 – 6) + 1(13)
= -21 + 8 + 13
= 0
So, the system has infinite solutions:
Let z = k,
So,
3x + y = -k
x – 4y = -3k
Now,
x = 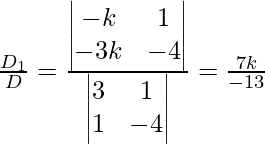
y = 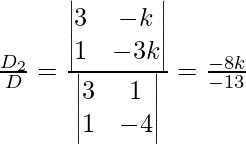
x = 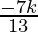
y = 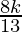
z = k
and there values satisfy equation 3
Hence, x = -7k, y = 8k, z = 13k
Question 4. Find the real values of λ for which the following system of linear equations has non-trivial solutions
2λx – 2y + 3z = 0
x + λy + 2z = 0
2x + λz = 0
Solution:
Finding the determinant
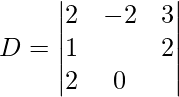
= 3λ3 + 2λ – 8 – 6λ
= 2λ3 – 4λ – 8
Which is satisfied by λ = 2 {for non-trivial solutions λ =2}
Now let z = k
4x – 2y = -3k
x + 2y = -3k
x = 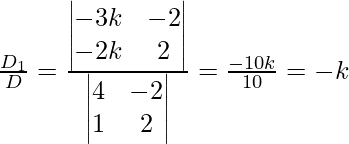
y =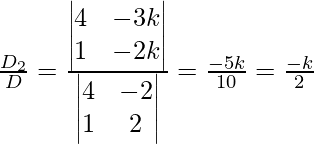
Hence, the solution is x = -k, y = 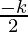 , z = k
, z = k
Question 5. If a, b, c are non-zero real numbers and if the system of equations
(a – 1)x = y + z
(b – 1)y = z + x
(c – 1)z = x + y
has a non-trivial solution, then prove that ab + bc + ca = abc
Solution:
Finding the determinant
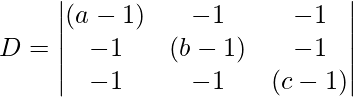
Now for non-trivial solution, D = 0
0 = (a – 1)[(b – 1)(c – 1) – 1]+1[-c + 1 – 1] + [-c + 1 – 1] – [ 1 + b – 1]
0 = (a – 1)[bc – b – c + 1 – 1] – c – b
0 = abc – ab -ac + b + c – c – b
ab + bc + ac = abc
Hence proved
Share your thoughts in the comments
Please Login to comment...