Class 12 RD Sharma Solutions – Chapter 6 Determinants Exercise Ex. 6.6 | Set 1
Last Updated :
07 Sep, 2021
Question 1. If A is a singular matrix, then find the value of |A|.
Solution:
Given that A is a singular matrix.
So, as we know if A is a n×n matrix and it is singular, the value of its determinant is always 0.
Thus, |A| = 0.
Question 2. For what value of x, the following matrix is singular?
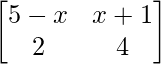
Solution:
Given that 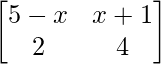
As we know if A is a n×n matrix and it is singular, so, the value of its determinant is always 0.
=> |A| = 0
=> 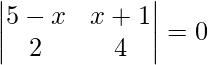
=> 4(5 – x) – 2(x + 1) = 0
=> 20 – 4x – 2x – 2 = 0
=> 18 – 6x = 0
=> 18 = 6x
=> x = 3
Therefore, the value of x is 3.
Question 3. Find the value of the determinant 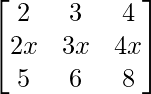 .
.
Solution:
Given that
A = 
|A| = 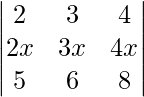
So, on taking out x common from R2 we get,
|A| = 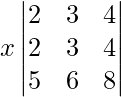
As R1 = R2, we get
|A| = 0
Therefore, the value of the determinant is 0.
Question 4. State whether the matrix 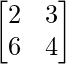 is singular or non-singular.
is singular or non-singular.
Solution:
Given that
A = 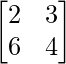
|A| = 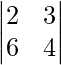
|A| = 2 (4) – 6 (3)
= 8 – 18
= -10
As we know if A is a n×n matrix and it is singular, so the value of its determinant is always 0.
As |A| = -10 here, the given matrix is non-singular.
Question 5. Find the value of the determinant 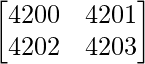 .
.
Solution:
Given that
A = 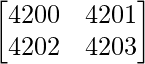
|A| = 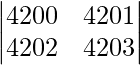
On applying C2 -> C2 – C1, we get
|A| = 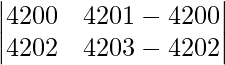
|A| = 
|A| = 4200 – 4202
|A| = -2
Therefore, the value of determinant is -2.
Question 6. Find the value of the determinant 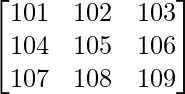 .
.
Solution:
Given that
A = 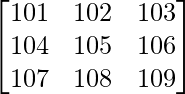
|A| = 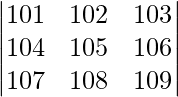
On applying C2 -> C2 – C1 and C3 -> C3 – C1, we get
|A| = 
|A| = 
On taking out 2 common from R3 we get,
|A| = 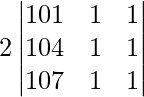
As R2 = R3, we get
|A| = 0
Therefore, the value of the determinant is zero.
Question 7. Find the value of the determinant 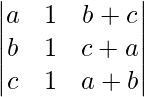 .
.
Solution:
Given that
A = 
|A| = 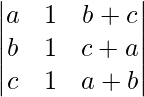
On applying C1 -> C1 + C3 we get,
= 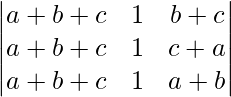
= 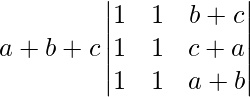
= (a + b + c) (0)
= 0
Therefore, the value of determinant is 0.
Question 8. If A = 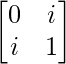 and B =
and B =  , find the value of |A| + |B|.
, find the value of |A| + |B|.
Solution:
Given that
A = 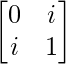
|A| = 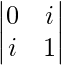
= 0 – i2
= – (-1)
= 1
Also, we have
B = 
|B| = 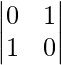
= 0 – 1
= -1
So,
|A| + |B| = 1 + (-1)
= 1 – 1
= 0
Therefore, the value of |A| + |B| is 0.
Question 9. If A = 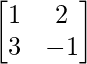 and B =
and B = 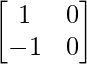 , find |AB|.
, find |AB|.
Solution:
We have,
A = 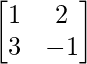 and B =
and B = 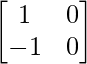
So, we get
AB = 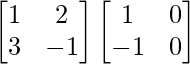
= 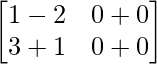
= 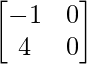
Now we have,
|AB| = 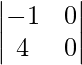
= -1 (0) – 0 (4)
= 0 – 0
= 0
Therefore, the value of |AB| is 0.
Question 10. Evaluate 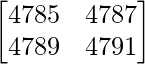 .
.
Solution:
Given that
A = 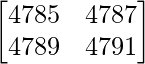
|A| = 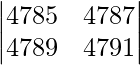
On applying C2 -> C2 – C1 we get,
|A| = 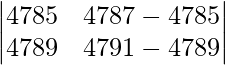
= 
On taking out 2 common from R2 we get,
= 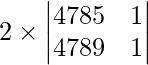
= 2 (4785 – 4789)
= 2 (-4)
= -8
Therefore, the value of the determinant is 0.
Question 11. If w is an imaginary cube root of unity, find the value of 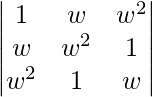 .
.
Solution:
Given that,
A = 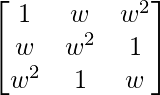
|A| = 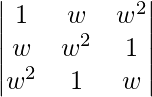
On applying C1 -> C1 + C_2 + C_3 we get,
= 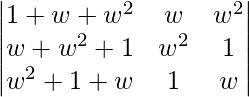
= 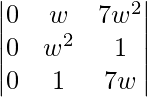
= 0
Question 12. If A = 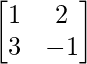 and B =
and B =  , find |AB|.
, find |AB|.
Solution:
Given that
A = 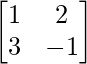
|A| = -1 – 6
= -7
B = 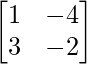
|B| = – 2 + 12
= 10
We know if A and B are square matrices of the same order, then we have,
=> |AB| = |A|. |B|
= (-7) (10)
= -70
Therefore, the value of |AB| is -70.
Question 13. If A = [aij] is a 3 × 3 diagonal matrix such that a11 = 1, a22 = 2 a33 = 3, then find |A|.
Solution:
Given that a11 = 1, a22 = 2 and a33 = 3.
If A is a diagonal matrix of order n x n, then we have
=> 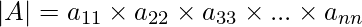
So, we get
|A| = 1 (2) (3)
= 6
Therefore, the value of |A| is 6.
Question 14. If A = [aij] is a 3 × 3 scalar matrix such that a11 = 2, then find the value of |A|.
Solution:
Given that A = [aij] which is a 3 × 3 scalar matrix and a11 = 2,
As we know that a scalar matrix is a diagonal matrix, in which all the diagonal elements are equal to a given scalar number.
=> A = 
= 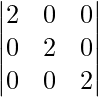
On expanding along C1, we get
= 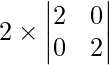
= 2 (2) (2)
= 8
Therefore, the value of |A| is 8.
Question 15. If I3 denotes an identity matrix of order 3 × 3, find the value of its determinant.
Solution:
As we know that in an identity matrix, all the diagonal elements are 1 and the remaining elements are 0.
Here,
I3 = 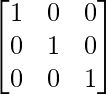
= 
On expanding along C1, we get
= 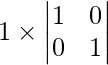
= 1
Therefore, the value of the determinant is 1.
Question 16. A matrix A of order 3 × 3 has determinant 5. What is the value of |3A|?
Solution:
Given that matrix A is of order 3 x 3 and the determinant = 5.
If A is a square matrix of order n and k is a constant, then we have
=> |kA| = kn |A|
Here,
Number of rows = n
Also, k is a common factor from each row of k.
Hence, we get
3A = 33 |A|
= 27 (5)
= 135
Therefore, the value of |3A| is 135.
Question 17. On expanding by the first row, the value of the determinant of 3 × 3 square matrix A = [aij] is a11 C11 + a12 C12 + a13 C13, where [Cij] is the cofactor of aij in A. Write the expression for its value on expanding by the second column.
Solution:
As we know that if a square matrix(let say A) is of order n, then the sum of the products of elements of a row or a column with their cofactors is always equal to det (A).
So,

Also, 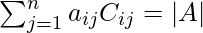
On expanding along R1 we get,
|A| = a11 C11 + a12 C12 + a13 C13
Now,
On expanding along C2 we get,
|A| = a12 C12 + a22 C22 + a32 C32
Question 18. On expanding by the first row, the value of the determinant of 3 × 3 square matrix A = [aij ] is a11 C11 + a12 C12 + a13 C13, where [Cij] is the cofactor of aij in A. Write the expression for its value on expanding by the second column.
Solution:
As we know that if a square matrix(let say A) is of order n, then the sum of the products of elements of a row or a column with their cofactors is always equal to det (A).
So,

Also, 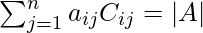
On expanding along R1 we get,
|A| = a11 C11 + a12 C12 + a13 C13
Now,
On expanding along C2 we get,
|A| = a12 C12 + a22 C22 + a32 C32 = 5
Share your thoughts in the comments
Please Login to comment...