Question 1. There are 6% defective items in a large bulk of items. Find the probability that a sample of 8 items will include not more than one defective item.
Solution:
Let us consider X be the number of defective items in a sample of 8 items.
So, a binomial distribution follows by x with n = 8.
and Probability of getting a defective item(p) = 0.06
The probability of getting a defective item (1 – p) = 0.94
So, P(X = r) = 8Cr (0.06)r (0 . 94 )8 – r, where r = 0, 1, 2, 3, . . . 8
So, the required probability is
= P (X < 1)
= P(X = 0) + P(X = 1)
= 8C0 (0.06)0 (0.94)8-0 + 8C1 (0.06)1 (0.94 )8-1
= (0.94)8 + 8 (0.06) (0.94)7
= (0.94)7 {0.94 + 0.48}
= 1.42 (0.94)7
Question 2. A coin is tossed 5 times. What is the probability of getting at least 3 heads?
Solution:
Let us consider X be the number of heads in 5 tosses.
So, a binomial distribution follows by x with n = 5
Probability of getting a head(p) = 1/2
And q = 1 – p = 1 – 1/2 = 1/2
P(X = r) = 5Cr (1/2)r (1/2)5-r , where r = 0, 1, 2 . . . 5
So, the required probability is
= P(X > 3)
= P(X = 3) + P(X = 4) + P(X = 5)
= 5C3 (1/2)3 (1/2)5-3 + 5C4 (1/2)1 (1/2)5-1 + 5C5 (1/2)5 (1/2)5-0
= 10 (1/2)5 + 5 (1/2)5 + 1 (1/2)5
= (1/2)5 (10 + 5 + 1)
= (1/2)5 (16)
= 1/2
Question 3. A coin is tossed 5 times. What is the probability that tail appears an odd number of times?
Solution:
Let us consider X be the number of tails when a coin is tossed 5 times.
So, a binomial distribution follows by x with n = 5
Probability of getting head(p) = 1/2.
Also, q = 1 – p = 1/2
P(X = r) = 5C3 (1/2)r (1/2)n-r = 5Cr (1/2)5
So, the required probability is
= P(X = 1) + P(X = 3) + P(X = 5)
= 5C1 (1/2)5 + 5C3 (1/2)5 + 5C5 (1/2)5
= (1/2)5 [5 + 10 + 1]
= 16/32
= 1/2
Question 4. A pair of dice is thrown 6 times. If getting a total of 9 is considered a success, what is the probability of at least 5 successes?
Solution:
Let us consider X be the number of successes in 6 throws of the two dice.
So the probability of success is equal to the probability of getting a total of 9
= Probability of getting (3, 6), (4, 5), (5, 4), (6, 3) from 36 outcomes
Here, p = 4/36 = 1/9
Also q = 1 – p = 8/9 and n = 6
Now, a binomial distribution X follows with n = 6, p = 1/9, and q = 8/9
P(X = r) = 6Cr (1/9)r (8/9)6-r
The required probability is
= P(X > 5)
= P(X = 5) + P(X = 6)
= 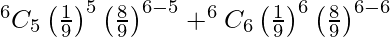
= 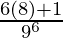
= 49/96
Question 5. A fair coin is tossed 8 times, find the probability:
(i) of exactly 5 heads.
Solution:
Let us consider X be the number of heads obtained when a fair is tossed 8 times.
Now, a binomial distribution X follows with n = 8.
Here, p = 1/2 and q = 1 – 1/2 = 1/2
So, P(X = r) = 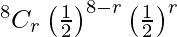
= 8Cr (1/2)8 , where r = 0, 1, 2, . . . , 8
So, the probability of obtaining exactly 5 heads is
P(X = 5) = 8C5 (1/2)8
= 56/256
= 7/32
(ii) of at least six heads.
Solution:
Let us consider X be the number of heads obtained when a fair is tossed 8 times.
Now, a binomial distribution X follows with n = 8.
Here, p = 1/2 and q = 1 – 1/2 = 1/2
So, P(X = r) = 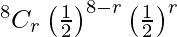
= 8Cr (1/2)8 , where r = 0, 1, 2, . . . , 8
So, the probability of obtaining exactly 5 heads is
P(X = 5) = 8C5 (1/2)8
= 56/256
= 7/32
(iii) of at most six heads.
Solution:
Let us consider X denotes the number of heads obtained when a fair is tossed 8 times.
Now, a binomial distribution X follows with n = 8.
Here p = 1/2 and q = 1 – 1/2 = 1/2
P(X = r) = 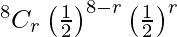
= 8Cr (1/2)8 , r = 0, 1, 2, . . . , 8
so the probability of obtaining at most 6 heads is
P (X < 6) = 1 – [P(X = 7) + P(X = 8)]
= ![Rendered by QuickLaTeX.com 1 - \left[ {}^8 C_7 \left( \frac{1}{2} \right)^8 +^8 C_8 \left( \frac{1}{2} \right)^8 \right]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-fb2cf1e11c0ba34c5ec64b2a0c794c9d_l3.png)
= 1 – (8/256 + 1/256)
= 1 – 9/256
= 247/256
Question 6. Find the probability of 4 turning up at least once in two tosses of a fair die.
Solution:
Let us consider X denotes the probability of getting 4 in two tosses of a fair die.
Now, a binomial distribution X follows with n = 2.
Here, p = 1/6 and q = 5/6
P(X = r) = 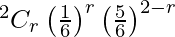
So, the probability of obtaining 4 at least once is
P(X > 1) = 1 – P(X = 0)
= 1 – 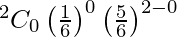
= 1 – 25/36
= 11/36
Question 7. A coin is tossed 5 times. What is the probability that head appears an even number of times?
Solution:
Let us consider X denotes the number of heads that appear when a coin is tossed 5 times.
Now, a binomial distribution X follows with n = 5
Here p = q = 1/2.
P(X = r) = 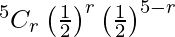
= 5Cr (1/2)5
P (head appears an even number of times) = P(X = 0) + P(X = 2) + P(X = 4)
= 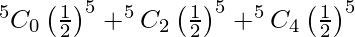
= 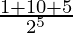
= 16/32
= 1/2
Question 8. The probability of a man hitting a target is 1/4. If he fires 7 times, what is the probability of his hitting the target at least twice?
Solution:
Let us consider X denotes the number of times the target is hit.
Now, a binomial distribution X follows with n = 7.
Here, p = 1/4 and q = 3/4.
P(X = r) = 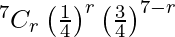
P(hit the target at least twice) = P(X > 2)
= 1 – {P(X = 0) + P(X = 1)}
= 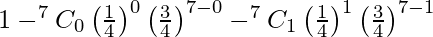
= 1 – (3/4)7 – 7 (1/4) (3/4)6
= 1 – 1/16384(2187 + 5103)
= 1 – 3645/8192
= 4547/8192
Question 9. Assume that on average one telephone number out of 15 called between 2 P.M. and 3 P.M. on weekdays is busy. What is the probability that if six randomly selected telephone numbers are called, at least 3 of them will be busy?
Solution:
Let us consider X denotes the number of busy calls for 6 randomly selected telephone numbers.
Now, a binomial distribution X follows with n = 6.
Here, p = one out of 15 = 1/15
And q = 1 – 1/15 = 14/15
P(X = r) = 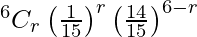
So, the probability that at least 3 of them are busy is
P(X > 3) = 1 – {P(X = 0) + P(X = 1) + P(X = 2)}
= 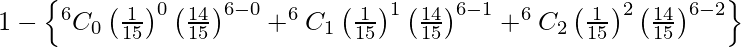
= 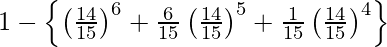
Question 10. If getting 5 or 6 in a throw of an unbiased die is a success and the random variable X denotes the number of successes in six throws of the die, find P (X ≥ 4).
Solution:
Let us consider X be the number of successes. That is getting 5 or 6 in a throw of die in 6 throws.
Now, a binomial distribution X follows with n = 6
Here, p = of getting 5 or 6 = 1/6 + 1/6 = 1/3
And q = 1 – p = 2/3
P(X = r) = 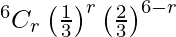
P(X > 4) = P(X = 4) + P(X = 5) + P(X = 6)
= 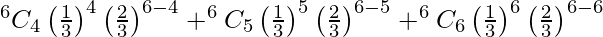
= (1/36) (60 + 12 + 1)
= 73/729
Question 11. Eight coins are thrown simultaneously. Find the chance of obtaining at least six heads.
Solution:
Let us consider X denotes the number of heads in tossing 8 coins.
Now, a binomial distribution X follows with n = 8.
Here, p = 1/2 and q = 1/2
P(X = r) = 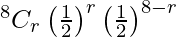
= 8Cr (1/2)8
So, the probability of getting at least 6 heads is
P(X > 6) = P(X = 6) + P(X = 7) + P(X = 8)
= 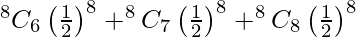
= 1/28(28 + 8 + 1)
= 37/256
Question 12. Five cards are drawn successively with replacement from a well-shuffled pack of 52 cards.
(i) What is the probability that all the five cards are spades?
Solution:
Let us consider X be the number of spade cards when 5 cards are drawn with replacement.
Now, a binomial distribution X follows with n = 5.
p = 13/52 = 1/4 and q = 1 – p = 3/4
P(X = r) = 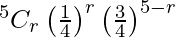
P(All cards are spades) = P(X = 5)
= 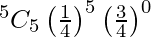
= 1/1024
(ii) What is the probability that only 3 cards are spades?
Solution:
Let us consider X be the number of spade cards when 5 cards are drawn with replacement.
Now, a binomial distribution X follows with n = 5.
Here, p = 13/52 = 1/4 and q = 1 – p = 3/4
P(X = r) = 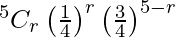
P(only 3 cards are spades) = P(X = 3)
= 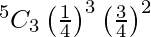
= (1/1024) (90)
= 45/512
(iii) What is the probability that none is a spade?
Solution:
Let us consider X be the number of spade cards when 5 cards are drawn with replacement.
Now, a binomial distribution X follows with n = 5.
Here p = 13/52 = 1/4 and q = 1 – p = 3/4.
P(X = r) = 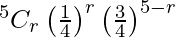
P(none is a spade) = P(X = 0)
= 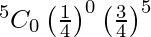
= 243/1024
Question 13. A bag contains 7 red, 5 white, and 8 black balls. Four balls are drawn one by one with replacement.
(i) What is the probability that none is white?
Solution:
Let us consider X denotes the number of white balls drawn when 4 balls are drawn with replacement.
Now, a binomial distribution X follows with n = 4.
Here, the probability for a white ball(p) = 5/20 = 1/4
And q = 1 – p = 3/4
P(X = r) = 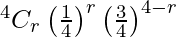
So, the probability that none is white is
P(X = 0) = 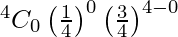
= 81/256
(ii) What is the probability that none is white?
Solution:
Let us consider X denotes the number of white balls drawn when 4 balls are drawn with replacement.
Now, a binomial distribution X follows with n = 4.
Here, the probability for a white ball(p) = 5/20 = 1/4
And q = 1 – p = 3/4
P(X = r) = 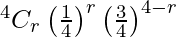
so, the probability that none is white is
P(X = 0) = 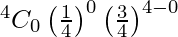
= 81/256
(iii) What is the probability that any two are white?
Solution:
Let us consider X denotes the number of white balls drawn when 4 balls are drawn with replacement.
Now, a binomial distribution X follows with n = 4.
So, the probability for a white ball(p) = 5/20 = 1/4
And q = 1 – p = 3/4
P(X = r) = 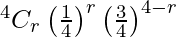
So, the probability that any two are white is
P(X = 2) = 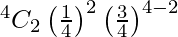
= 54/256
= 27/128
Question 14. A box contains 100 tickets, each bearing one of the numbers from 1 to 100. If 5 tickets are drawn successively with replacement from the box, find the probability that all the tickets bear numbers divisible by 10.
Solution:
Let us consider X denotes the variable representing number on the ticket bearing a number divisible by 10 out of the 5 tickets drawn.
Now, a binomial distribution X follows with n = 5.
Here, the probability of getting a ticket bearing number divisible by 10(p) = 10/100
= 1/10
And q = 1 – p = 9/10
P(X = r) = 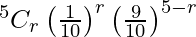
So, the probability that all the tickets bear numbers divisible by 10 is
P(X = 5) = 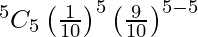
= (1/10)5 (9/10)0
= (1/10)5
Question 15. A bag contains 10 balls, each marked with one of the digits from 0 to 9. If four balls are drawn successively with replacement from the bag, what is the probability that none is marked with the digit 0?
Solution:
Let us consider X denotes the number of balls marked with the digit 0 when 4 balls are drawn successfully with replacement.
Now, a binomial distribution X follows with n = 4.
So, the probability that a ball randomly drawn bears digit 0(p) = 1/10
And q = 1 – p = 9/10
P(X = r) = 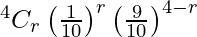
P(none bears the digit 0) = P(X = 0)
= 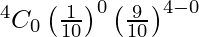
= (9/10)4
Question 16. In a large bulk of items, 5 percent of the items are defective. What is the probability that a sample of 10 items will include not more than one defective item?
Solution:
Let us consider X be the number of defective items in a sample of 10 items.
Now, a binomial distribution X follows with n = 10.
And the probability of defective items(p) = 5% = 0.05
And q = 1 – p = 0.95
P(X = r) = 10Cr (0. 05)r (0.95)10-r
So, the probability(sample of 10 items will include not more than one defective item) is
P(X < 1) = P(X = 0) + P(X = 1)
= 10C0 (0.05)0 (0.95 ){0-0 + 10C1 (0.05)1 (0.95)10-1
= (0.95)9 (0.95 + 0.5)
= 1.45 (0.95)9
Question 17. The probability that a bulb produced by a factory will fuse after 150 days of use is 0.05.
(i) Find the probability that out of 5 such bulbs none will fuse after 150 days of use.
Solution:
Let us consider X be the number of bulbs that fuse after 150 days.
Now, a binomial distribution X follows with n = 5.
Here, p = 0.05 and q = 0.95
Or p = 1/20 and q = 19/20
P(X = r) = 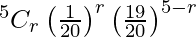
So, the probability (none will fuse after 150 days of use) is
P(X = 0) = 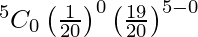
= (19/20)5
(ii) Find the probability that out of 5 such bulbs, not more than one will fuse after 150 days of use.
Solution:
Let us consider X denotes the number of bulbs that fuse after 150 days.
Now, a binomial distribution X follows with n = 5.
Here p = 0.05 and q = 0.95.
Or p = 1/20 and q = 19/20
P(X = r) = 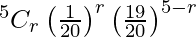
So, the probability (not more than 1 will fuse after 150 days of use) is
P(X < 1) = P(X = 0) + P(X = 1)
= 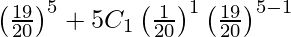
= 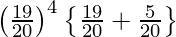
= (6/5) (19/20)4
(iii) Find the probability that out of 5 such bulbs more than one will fuse after 150 days of use
Solution:
Let us consider X denotes the number of bulbs that fuse after 150 days.
Now, a binomial distribution X follows with n = 5.
Here p = 0.05 and q = 0.95
Or p = 1/20 and q = 19/20
P(X = r) = 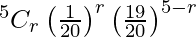
So, the probability(more than one will fuse after 150 days of use) is
P(X > 1) = 1 – P(X < 1)
= 1 – (6/5) (19/20)4
(iv) Find the probability that out of 5 such bulbs at least one will fuse after 150 days of use.
Solution:
Let us consider X denotes the number of bulbs that fuse after 150 days.
Now, a binomial distribution X follows with n = 5.
Here p = 0.05 and q = 0.95
Or p = 1/20 and q = 19/20
P(X = r) = 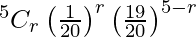
So, the probability(at least one will fuse after 150 days of use) is
P(X > 1) = 1 – P(X = 0)
= 1 – (19/20)5
Question 18. Suppose that 90% of people are right-handed. What is the probability that at most 6 of a random sample of 10 people are right-handed?
Solution:
Let us consider X denotes the number of people that are right-handed in the sample of 10 people.
Now, a binomial distribution X follows with n = 10.
Here p = 90 % = 90/100 = 0.9
And q = 1 – p = 0.1
P(X = r) = 10Cr (0.9)r (0.1)10-r
So, the probability that at most 6 are right – handed is
P(X < 6) = P(X = 0) + P(X = 1) + P(X = 2) + P(X = 3) + P(X = 4) + P(X = 5) + P(X = 6)
= 1 – {P(X = 7) + P(X = 8) + P(X = 9) + P(X = 10)}
= 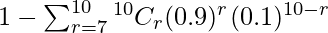
Share your thoughts in the comments
Please Login to comment...