Question 15. From a pack of 52 cards, 4 cards are drawn at random. Find the probability that cards drawn are of the same color?
Solution:
From a pack of 52 cards, 4 cards are drawn
Hence, Sample space, n(S) = 52C4 -(1)
Let A be the event of getting cards of same color,
Since there are two sets of same color,
n(A) = 2 * 26C4 -(2)
P(A) = 2 * 26C4/52C4
= 92/833
Note: The factorial of the respective cases will give a large number,
so in such cases simplify the factorial in final step
Question 16. 100 students appeared for the two examinations, 60 passed the first, 50 passed the second and 30 passed both of the examinations. Find the probability that a student selected at random has at least passed one exam?
Solution:
There are 100 students. Hence, sample space will be –
n(S) = 100 -(1)
Let A be the event that 60 students passed in first exam,
n(A) = 60
= 60/100 -(2)
Let B be the event that 50 students passed in first exam,
n(A) = 50
= 50/100 -(3)
30 passed both of the examinations,
P(A ∩ B) = 30/100 -(4)
P(A ∪ B) = P(A) + P(B) – P(A ∩ B)
= 60/100 + 50/100 – 30/100 -(From 2, 3, 4)
= 4/5
Question 17. A box contains 10 white, 6 red, and 10 black balls. A ball is drawn at random from the box, what is the probability that ball is red or white?
Solution:
There are 10 white, 6 red and 10 black balls, hence the sample space will be,
n(S) = 10 + 6 + 10
= 26
Let W be the event of drawing the White balls,
n(W) = 10
P(W) = 10/26 -(1)
Let R be the event of drawing the Red balls,
n(R) = 6
P(R) = 6/26 -(2)
E & R are mutually exclusive events –
n(R ∩ E) = 0 -(red and white balls can’t be drawn to be together)
P(E ∪ R) = P(E) + P(R) – P(E ∩ R)
= 10/26 + 6/26
= 16/26
= 8/13
Question 18. In a race, the odds in favor of the horses A, B, C, D are 1 : 3, 1:4, 1:5 & 1:6. Find probability which one of them wins the race?
Solution:
We have P(A) : 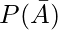 = 1 : 3
= 1 : 3
= P(A) / 1 – P(A) -(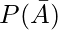 = 1 – P(A))
= 1 – P(A))
= 1/4 -(1)
Similarly P(B) = 1/5 -(2)
P(C) = 1/6 -(3)
P(D) = 1/7 -(4)
Probability that at least one of the horse wins is P(A ∪ B ∪ C ∪ D)
= 1/4 + 1/5 + 1/6 + 1/7 -(From 1, 2, 3, 4)
= 319/420
Question 19. The probability that a person will travel by train is 3/5 and probability that he will travel by plane is 1/4. Find the probability that he will travel by train or plane ?
Solution:
Let T be the event that persons travels by train –
P(T) = 3/5 -(1)
Let A be the event that persons travels by PLANE –
P(A) = 1/4 -(2)
P(A ∪ T) = P(A) + P(T) -((A ∩ T) = 0)
= 3/5 + 1/4 -(From 1 , 2)
= 17/20
Question 20. Two cards are drawn from a well-shuffled pack of 52 cards. Find the probability that both cards are black or king?
Solution:
Two cards are drawn from well shuffled deck of 52 cards,
n(S) = 52C2 -(1)
Let A be the event of getting black cards,
n(A) = 26C2
P(A) =26C2/52C2 -(2)
Let B be the event of getting KING cards,
n(B) = 4C2
P(B) = 4C2/52C2 -(3)
Also, n(A ∩ B) = 2C2
P(A ∩ B) = 2/52C2 -(4)
Now,
P(A ∪ B) = P(A) + P(B) – P(A ∩ B)
= 26 * 25/52 * 51 + 4 * 3 / 52 * 51 – 2/52 * 51
= 55/221
Question 21. In an entrance test graded on basis of two examination, the probability of randomly chosen student passing in exam 1 is 0.8 & the probability of passing in second examination is 0.7. The probability of passing in the one of the examination is 0.95. What is probability of passing in both?
Solution:
Let A be the event of selecting a random student who passed in examination 1,
P(A) = 0.8 -(1)
Let A be the event of selecting a random student who passed in examination 2,
P(B) = 0.7 -(2)
Now,
The probability of selecting a random student passing in at least one of the examination is –
P(A ∪ B) = 0.95 -(3)
Probability of passing both of the examination is P(A ∩ B),
P(A ∩ B) = P(A) + P(B) -P(A ∪ B)
= 0.8 + 0.7 – 0.95
=1.5-0.95
=0.55
Question 22. A box contains 40 nuts & 30 bolts. Half of the bolts and nuts are rusted. If two items are drawn at random, what is probability that they are rusted and both are bolts?
Solution:
A box contains 40 nuts and 30 bolts,
half of them are rusted –
=> 40/2 = 20 nuts are rusted
=> 30/2 = 15 bolts are rusted
Since two items are drawn,
Sample space n(S) = 70C2 -(1)
Let A be the event of choosing the rusted item –
n(A) = 35C2. -(20 nuts + 15 bolt = 35)
P(A) = 35C2/70C2
35 * 34/ 70 * 69 -(2)
Let B be the event of choosing two rusted bolts-
n(B) = 30C2
P(B) = 30C2/70C2
= 30 * 29 / 70 * 69 -(3)
Also, n(A n B) = 15 -(bolts are rusted)
P(A n B) = 15*14/70* 69 -(4)
Now,
P(A ∪ B) = P(A) + P(B) – P(A ∩ B)
= (35*34/70*69) + (30*29/70*69) – (15*14/70*69) -(From 2, 3, 4)
= 185/483
Question 23. A integer is chosen at random from first 200 integers, find the probability that the integer is divisible by 6 or 8?
Solution:
A integer is chosen at random from 200 integers,
SAMPLE SPACE = n(S) = 200 -(1)
Let A be the event of choosing a number divisible by 6,
n(A) ={6,12,18. . . 198}
n(A) = 33 (Using T n formula)
P(A) = 33/200 -(2)
Let B be the event of choosing a number divisible by 8,
n(B) = {8,16,24. . . 200}
n(B) = 25
P(B) = 25/200
= 1/4 -(3)
Also, n(A n B)= {24,48. . 192}
= 8
P(A n B) = 8/200 -(4)
Now,
P(A ∪ B) = P(A) + P(B) – P(A ∩ B)
= 1/4 -(from 2, 3, 4)
Question 24. Find the probability of getting 2 or 3 tails, when a coin is tossed 4 times?
Solution:
A coin is tossed 4 times,
Hence, Sample space – n(S) = 2 4 =16
Let A be the event of getting 2 tails,
A = {HHTT, HTHT, TTHH, THTH, THHT, HTTH}
n(A) = 6
P(A) = 6/16 -(1)
Let B the event of getting 3 tails,
B = {HTTT, THTT, TTHT, TTTH}
n(B) = 4
P(B) = 4/16 -(2)
A & B are the mutually exclusive events-
Hence, P(A ∩ B) = 0
P(A ∪ B) = P(A) + P(B) – P(A ∩ B)
= 6/16 + 4/16-0
= 10/16
= 5/8
Question 25. Suppose a integer is choose from 1 to 1000, find the probability that it is multiple of 2 or 9?
Solution:
A number is chosen from 1 to 1000,
Hence, sample space, n(S) = 1000
Number of multiples of 2 from 1 to 1000 are – 500
Number of multiples of 9 from 1 to 1000 are – 111
Out of 111, 55 are even numbers
Hence, total number multiple of 2 or 9 – 500 + 56
Probability of number multiple of 2 or 9 –
= 556/1000
= 0.556
Question 26. In a metropolitan area the probabilities are 0.87, 0.36 & 0.30, that a family owns a color television set, a black and white TV or both. What is probability that family owns one of the set?
Solution:
Let A be the probability of a family having a color TV set,
P(A) = 0.87 -(1)
Let B be the probability of a family having a black and white TV set,
P(B) = 0.36 -(2)
Also, P(A ∩ B) = 0.3
P(A ∪ B) = P(A) + P(B) – P(A ∩ B)
= 0.87 + 0.36 – 0.30
= 0.93
Question 27. If A and B are mutually exclusive events, such that P(A) = 0.35 and P(B) = 0.45 find,
(i) P(A ∪ B)
(ii) P(A ∩ B)
(iii) 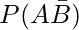 [Tex] [/Tex]
[Tex] [/Tex]
(iv) 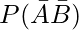
*** QuickLaTeX cannot compile formula:
*** Error message:
Error: Nothing to show, formula is empty
Solution:
(i) P(A ∪ B) = P(A) + P(B) (A and B are mutually exclusive events
i.e P( A∩ B) = 0)
= 0.80
(ii) P(A ∩ B)
P(A ∩ B) = 0 (A and B are mutually exclusive events)
(iii) 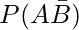 = P(A)
= P(A)
= 0.35
(iv) 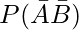 = 1 – P(A ∪ B)
= 1 – P(A ∪ B)
= 1 – 0.80
= 0.20
Question 28. A sample space consist of 9 elementary events, E1, E2, E3. . . E9, whose probabilities are P(E1) = P(E2) = 0.08, P(E3) = P(E4) = 0.1,P(E6) = P(E7) = 0.2,P(E8) = P(E9) = 0.07, suppose A = {E1, E5, E8}, B ={E2, E5, E8, E9}
(i) compute P(A), P(B) & P(A ∩ B)
(ii) Find P(A ∪ B)
(iii) List the combustion of the event A ∪ B, and find P(A ∪ B)
(iv) Calculate
*** QuickLaTeX cannot compile formula:
*** Error message:
Error: Nothing to show, formula is empty
Solution:
Given: P(E1) = P(E2) = 0.08, P(E3) = P(E4) = 0.1, P(E6) = P(E7) = 0.2, P(E8) = P(E9) = 0.07
Suppose: A = {E1, E5, E8}, B ={E2, E5, E8, E9} -(I)
Bc = {E1,E3,E4,E6.E7}
P(E5) = 1 – (0.08 + 0.1 + 0.2 + 0.07}
=0.1
(i) P(A) = 0.08 + 0.1 + 0.07 (From Given)
= 0.25
P(B) = 0.08 + 0.1 + 0.07 + 0.07
= 0.32
P(A ∩ B) = 0.1 + 0.07
= 0.17
(ii) P(A ∪ B) = P(A) + P(B) – P(A ∩ B)
= 0.57-0.17
= 0.40
(iii) 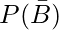 = 1 – P(B)
= 1 – P(B)
= 1 -0.32
= 0.68
Like Article
Suggest improvement
Share your thoughts in the comments
Please Login to comment...