Class 12 RD Sharma Solutions – Chapter 29 The Plane – Exercise 29.13
Last Updated :
18 Feb, 2022
Question 1. Show that 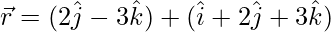 and
and 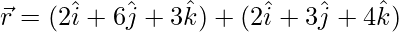 are coplanar. Also, find the equation of the plane containing them.
are coplanar. Also, find the equation of the plane containing them.
Solution:
We know, the lines 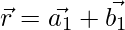 and
and 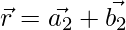 are coplanar if:
are coplanar if:

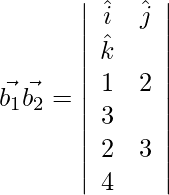
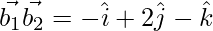
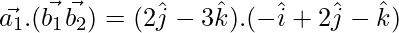

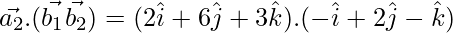
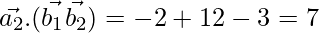
Since, 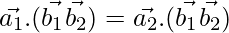 , the lines are coplanar.
, the lines are coplanar.
Equation of the plane containing them: 
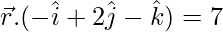
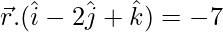
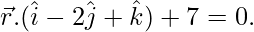
Question 2. Show that the lines 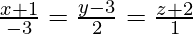 and
and 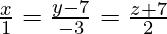 are coplanar. Also, find the equation of the plane containing them.
are coplanar. Also, find the equation of the plane containing them.
Solution:
We know the lines 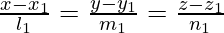 and
and 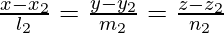 are coplanar if,
are coplanar if,

So, 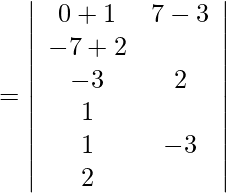
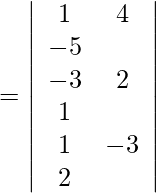
= 1(4 + 3) − 4(−6 − 1) − 5(9 − 2)
= 7 + 28 − 35
= 0.
So the lines are coplanar.
Equation of the plane: 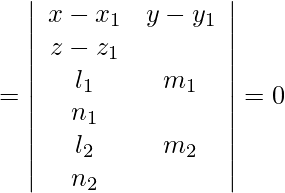
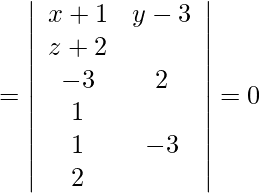
⇒ 7x + 7y + 7z = 0.
Question 3. Find the equation of the plane containing the line 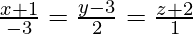 and the point (0,7,-7) and show that the line
and the point (0,7,-7) and show that the line 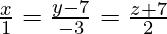 also lies in the same plane.
also lies in the same plane.
Solution:
We know the equation of a plane passing through a point (x1,y1,z1) is given by
a(x−x1) + b(y−y1) + c(z−z1) = 0 ……..(1)
Since the required plane passes through (0,7,-7), the equation becomes
ax + b(y − 7) + c(z + 7) = 0 …….(2)
It also contains 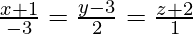 and point is (−1,3,−2).
and point is (−1,3,−2).
a(−1) + b(3 − 7) + c(−2 + 7) = 0
⇒ −a − 4b + 5c = 0
Also, −3a + 2b + c = 0
Solving the equations, we get x + y + z = 0
So, 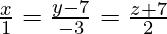 lies on the plane x + y + z = 0.
lies on the plane x + y + z = 0.
Question 4. Find the equation of the plane which contains two parallel lines 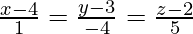 and
and 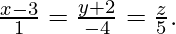
Solution:
We know the equation of a plane passing through a point (x1,y1,z1) is given by
a(x−x1) + b(y−y1) + c(z−z1) = 0 ……..(1)
The required plane passes through (4,3,2). Hence,
a(x − 4) + b(y − 3) + c(z − 2) = 0
It also passes through (3,-2,0). Hence,
a(3 − 4) + b(−2 − 3) + c(0 − 2) = 0
⇒ a + 5b + 2c = 0 …….(2)
Also, a − 4b + 5c = 0 ……..(3)
Solving (2) and (3) by cross multiplication, we get the equation of the plane as:
⇒ 11x − y − 3z − 35 = 0.
Question 5. Show that the lines 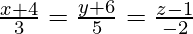 and 3x − 2y + 5 = 0 = 2x + 3y + 4z − 4 intersect. Find the equation of the plane.
and 3x − 2y + 5 = 0 = 2x + 3y + 4z − 4 intersect. Find the equation of the plane.
Solution:
Using a1a2 + b1b2 + c1c2 = 0, we get
3a − 2b + c = 0 ….(1)
Also, 2a + 3b + 4c = 0. ….(2)
Solving (1) and (2) by cross multiplication, we have
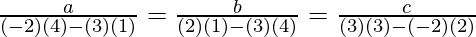
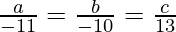
Hence, the equation of the plane is 45x − 17y + 25z + 53 = 0
and the point of intersection is (2,4,−3).
Question 6. Show that the plane whose vector equation is 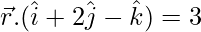 contains the line whose vector equation is
contains the line whose vector equation is 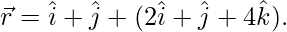
Solution:
Here, 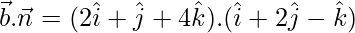
= 2(1) +1(2) + 4(−1)
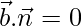
Now, 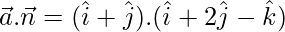
= 1(1) + 1(2) + 0(−1)
= 3
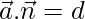
Hence, the given line lies on the plane.
Question 7. Find the equation of the plane determined by the intersection of the lines 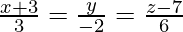 and
and 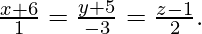
Solution:
Let the plane be ax + by + cz + d = 0
Since the plane passes through the intersection of the given lines, normal of the plane is perpendicular to the two lines.
⇒ 3a − 2b + 6c = 0
and, a − 3b + 2c = 0
Using cross multiplication, we have

⇒ 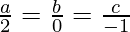
Question 8. Find the vector equation of the plane passing through the points (3,4,2) and (7,0,6) and perpendicular to the plane 2x − 5y − 15 = 0. Also, show that the plane thus obtained contains the line 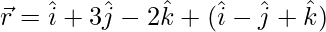
Solution:
Let the equation of the plane be 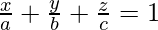
Since the plane passes through (3,4,2) and (7,0,6), we have
 and
and 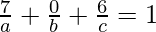
Since the required plane is perpendicular to 2x − 5y − 15 = 0, we have,
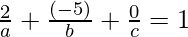
⇒ b = 2.5a
Substituting the value of b in the above equations we have,
 and
and 
Solving the above equations, we have
a = 17/5, b = 17/2 and c = −17/3.
Substituting the values in the equation of plane, we obtain
5x + 2y − 3z = 17.
Vector equation of the plane becomes: 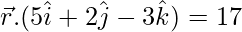 .
.
Question 9. If the lines  and
and 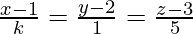 are perpendicular, find the values of k and also the equation the plane containing these lines.
are perpendicular, find the values of k and also the equation the plane containing these lines.
Solution:
The direction ratios of the two lines are r1 = (−3,−2k,2) and r2 = (k,1,5).
Since the lines are perpendicular, we have
(−3,−2k,2).(k,1,5) = 0
⇒ 3k + 2k − 10 = 0
⇒ 5k = 10
⇒ k = 2
Now, equation of the plane containing the lines is: 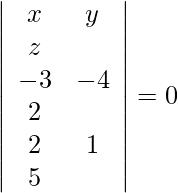
⇒ −22x + 19y + 5z + 31 = 0.
Question 10. Find the coordinates of the point where the line 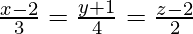 intersects the plane x − y + z − 5 = 0. Also, find the angle between the line and the plane.
intersects the plane x − y + z − 5 = 0. Also, find the angle between the line and the plane.
Solution:
Any point on the given line is of the form (3k + 2, 4k − 1, 2k + 2).
We have, (3k + 2) − (4k − 1) + (2k + 2) − 5 = 0
⇒ k = 0.
Thus, the coordinates of the point become (2,−1,2).
Let v be the angle between the line and the plane. Then,

Here, l = 3, m = 4, n =2, a =1, b = −1, c = 1.
Hence, 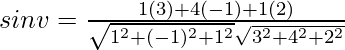
⇒ 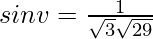
⇒ ![Rendered by QuickLaTeX.com v=sin^{-1}[\frac{1}{\sqrt3\sqrt29}]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-a89f8b88a8a5711a51098db1d3e59ac0_l3.png)
Question 11. Find the vector equation of the plane passing through three points with position vectors 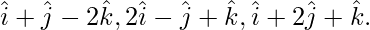
Solution:
Let A, B and C be the three given vectors respectively.

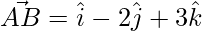
and, 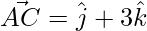
Now, 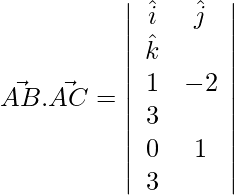
⇒ 
Equation of the plane is: 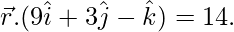
Coordinates of the points are (1,1,−2).
Question 12. Show that the lines 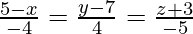 and
and 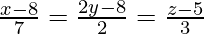 are coplanar.
are coplanar.
Solution:
We know the lines 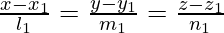 and
and 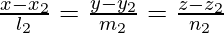 are coplanar if,
are coplanar if,

or, 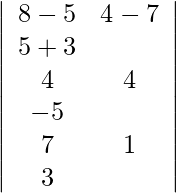
= 
= 3(12 + 5) + 3(12 + 35) + 8(4 − 28)
= 0.
Hence the lines are coplanar.
Question 13. Find the equation of the plane which passes through the point (3,2,0) and contains the line 
Solution:
Required equation of the plane passing through (3,2,0) is:
a(x − 3) + b(y − 2) + cz = 0 ……(1)
Since the plane also passes through the given line, we have
4b + 4c = 0 ……(2)
Also, the plane will be parallel so,
a + 5b + 4c = 0 ……(3)
Solving (2) and (3), we have
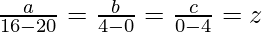
⇒ 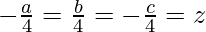
⇒ a = −z, b = z and c = −z
Putting the values in (1), we have
x − y + z − 1 = 0.
Share your thoughts in the comments
Please Login to comment...