Question 1. Find the slopes of the tangent and the normal to the following curves at the indicated points:
(i) y = √x3 at x = 4
(ii) y = √x at x = 9
(iii) y = x3 – x at x = 2
(iv) y = 2x2 + 3 sin x at x = 0
(v) x = a(θ – sin θ), y = a(1 + cos θ) at θ = –π/2
(vi) x = a cos3 θ, y = a sin3 θ at θ = π/4
(vii) x = a(θ – sin θ), y = a(1 – cos θ) at θ = π/2
(viii) y = (sin 2x + cot x + 2)2 at x = π/2
(ix) x2 + 3y + y2 = 5 at (1, 1)
(x) xy = 6 at (1, 6)
Solution:
We know that the slope of the tangent of a curve is given by dy/dx.
And slope of the normal = –1/slope of tangent = –1/(dy/dx).
(i) y = √x3 at x = 4
Differentiating y = √x3 with respect to x, we get,
Slope of tangent = 3x1/2/2
At x = 4, slope of tangent becomes,
Slope of tangent = 3(4)1/2/2 = 3(2)/2 = 3
And slope of normal at x = 4 is –1/3.
(ii) y = √x at x = 9
Differentiating y = √x with respect to x, we get,
Slope of tangent = x–1/2/2
At x = 9, slope of tangent becomes,
Slope of tangent = 9–1/2/2 = 1/[(3)(2)] = 1/6
And slope of normal at x = 9 is –6.
(iii) y = x3 – x at x = 2
Differentiating y = x3 – x with respect to x, we get,
Slope of tangent = 3x2 – 1
At x = 2, slope of tangent becomes,
Slope of tangent = 3(2)2 – 1 = 3(4) – 1 = 11
And slope of normal at x = 2 is –1/11.
(iv) y = 2x2 + 3 sin x at x = 0
Differentiating y = 2x2 + 3 sin x with respect to x, we get,
Slope of tangent = 4x + 3 cos x
At x = 0, slope of tangent becomes,
Slope of tangent = 4(0) + 3 cos 0 = 3.
And slope of normal at x = 0 is –1/3.
(v) x = a (θ – sin θ), y = a (1 + cos θ) at θ = –π/2
Differentiating x = a (θ – sin θ) with respect to θ, we get,
=> dx/dθ = a (1 – cos θ) . . . . (1)
Differentiating y = a (1 + cos θ) with respect to θ, we get,
=> dy/dθ = a (–sin θ) . . . . (2)
Dividing (2) by (1), we get,
dy/dx = Slope of tangent = –sin θ/(1 – cos θ)
At θ = –π/2, slope of tangent becomes,
Slope of tangent = –sin (–π/2)/(1 – cos (–π/2))
= 1/(1–0)
= 1
And slope of normal at θ = –π/2 is –1.
(vi) x = a cos3 θ, y = a sin3 θ at θ = π/4
Differentiating x = a cos3 θ with respect to θ, we get,
=> dx/dθ = a [(3cos2 θ) (–sin θ)]
= –3a cos2 θ sin θ . . . . (1)
Differentiating y = a sin3 θ with respect to θ, we get,
=> dy/dθ = a [(3sin2 θ) (cos θ)]
= 3a sin2 θ cos θ . . . . (2)
Dividing (2) by (1), we get,
dy/dx = Slope of tangent =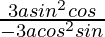 = – tan θ
= – tan θ
At θ = π/4, slope of tangent becomes,
Slope of tangent = – tan (π/4)
= −1
And slope of normal at θ = π/4 is 1.
(vii) x = a (θ – sin θ), y = a (1 – cos θ) at θ = π/2
Differentiating x = a (θ – sin θ) with respect to θ, we get,
=> dx/dθ = a (1 – cos θ) . . . . (1)
Differentiating y = a (1 – cos θ) with respect to θ, we get,
=> dy/dθ = a (sin θ) . . . . (2)
Dividing (2) by (1), we get,
dy/dx = Slope of tangent = sin θ/(1−cosθ)
= – tan θ
At θ = π/2, slope of tangent becomes,
Slope of tangent = sin π/2/(1−cos π/2)
= 1/(1−0)
= 1
And slope of normal at θ = π/2 is −1.
(viii) y = (sin 2x + cot x + 2)2 at x = π/2
Differentiating y = (sin 2x + cot x + 2)2 with respect to x, we get,
Slope of tangent = 2 (sin 2x + cot x + 2) (2 cos 2x – cosec2 x)
At x = π/2, slope of tangent becomes,
Slope of tangent = 2 (sin 2(π/2) + cot π/2 + 2) (2 cos 2(π/2) – cosec2 (π/2))
= 2 (0 + 0 + 2) (–2 – 1)
= –12
And slope of normal at x = π/2 is 1/12.
(ix) x2 + 3y + y2 = 5 at (1, 1)
Differentiating x2 + 3y + y2 = 5 with respect to x, we get,
=> 2x + 3 (dy/dx) + 2y (dy/dx) = 0
=> 2x + dy/dx (2y+3) = 0
=> Slope of tangent = dy/dx = –2x/(2y+3)
At x = 1 and y = 1, slope of tangent becomes,
Slope of tangent = –2(1)/[2(1)+3] = –2/5
And slope of normal at (1, 1) is 5/2.
(x) xy = 6 at (1, 6)
Differentiating xy = 6 with respect to x, we get,
=> x (dy/dx) + y = 0
=> Slope of tangent = dy/dx = –y/x
At x = 1 and y = 6, slope of tangent becomes,
Slope of tangent = –6/1 = –6
And slope of normal at (1, 6) is 1/6.
Question 2. Find the values of a and b if the slope of the tangent to the curve xy + ax + by = 2 at (1, 1) is 2.
Solution:
We know that the slope of the tangent of a curve is given by dy/dx.
Differentiating xy + ax + by = 2 with respect to x, we get
=> x (dy/dx) + y + a + b (dy/dx) = 2
=> dy/dx = −(a+y)/(x+b)
As we are given dy/dx = 2, we get,
=> −(a+y)/(x+b) = 2
Now at x = 1 and y = 1, we get,
=> −(a+1)/(1+b) = 2
=> −a − 1 = 2 + 2b
=> a + 2b = –3 . . . . (1)
Now the point (1, 1) also lies on the curve, so we have,
=> 1 × 1 + a × 1 + b × 1 = 2
=> 1 + a + b = 2
=> a + b = 1 . . . . (2)
Subtracting (1) from (2), we get,
=> –b = 1+3
=> b = –4
Putting b = –4 in (1), we get,
=> a = 1+4 = 5
Therefore, the value of a is 5 and b is –4.
Question 3. If the tangent to the curve y = x3 + ax + b at (1, –6) is parallel to the line x – y + 5 = 0, find a and b.
Solution:
We know that the slope of the tangent of a curve is given by dy/dx.
Differentiating y = x3 + ax + b with respect to x, we get
=> dy/dx = 3x2 + a
Now at x = 1 and y = –6, we get,
=> dy/dx = 3(1)2 + a
=> dy/dx = 3 + a . . . . (1)
Now this curve is parallel to the line x – y + 5 = 0.
=> y = x + 5
Therefore slope of the line is 1. So, the slope of the curve will also be 1 as slope of parallel lines are equal. So, from (1), we get,
=> dy/dx = 1 . . . . (2)
From (1) and (2), we get,
=> a + 3 = 1
=> a = –2 . . . . (3)
Now at x = 1 and y = –6, our curve y = x3 + ax + b becomes,
=> –6 = 1 + a + b
=> a + b = –7
Using (3), we get,
=> b = –7 – (–2)
=> b = –5
Therefore, the value of a is –2 and b is –5.
Question 4. Find a point on the curve y = x3 – 3x where the tangent is parallel to the chord joining (1, – 2) and (2, 2).
Solution:
We are given the coordinates of the chord (1, – 2) and (2, 2).
Therefore, slope of the chord =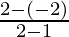 = 4
= 4
Given curve is y = x3 – 3x. We know that the slope of the tangent of a curve is given by dy/dx.
=> dy/dx = 3x2 – 3
As the tangent is parallel to the chord, its slope must be equal to 4.
=> 3x2 – 3 = 4
=> 3x2 = 7
=> x =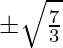
Putting value of x in the curve y = x3 – 3x, we get
=> y = x (x2 – 3)
=> y =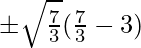
=> y =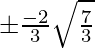
Therefore, the required point is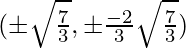 .
.
Question 5. Find a point on the curve y = x3 – 2x2 – 2x at which the tangent lines are parallel to the line y = 2x – 3.
Solution:
Given curve is y = x3 – 2x2 – 2x. We know that the slope of the tangent of a curve is given by dy/dx.
=> dy/dx = 3x2 – 4x – 2 . . . . (1)
Now this curve is parallel to the line y = 2x – 3 whose slope is 2. So, the slope of the curve will also be 2. So, from (1), we get,
=> 3x2 – 4x – 2 = 2
=> 3x2 – 6x + 2x – 4 = 0
=> 3x (x – 2) + 2 (x – 2) = 0
=> (x – 2) (3x + 2) = 0
=> x = 2 or x = –2/3
If x = 2, we get
y = (2)3 – 2 × (2)2 – 2 × (2)
= 8 – 8 – 4
= – 4
And if x = –2/3, we get,
y = (–2/3)3 – 2 × (–2/3)2 – 2 × (–2/3)
=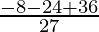
= 4/27
Therefore, (2, –4) and (–2/3, 4/27) are the required points.
Question 6. Find a point on the curve y2 = 2x3 at which the slope of the tangent is 3.
Solution:
Given curve is y2 = 2x3. We know that the slope of the tangent of a curve is given by dy/dx.
=> 2y dy/dx = 6x2
=> dy/dx = 3x2/y . . . . (1)
As it is given that the slope of tangent is 3, we get,
=> 3x2/y = 3
=> 3x2 = 3y
=> x2 = y
Putting this in the curve y2 = 2x3, we get,
=> (x2)2 = 2x3
=> x4 − 2x3 = 0
=> x3 (x − 2) = 0
=> x = 0 or x = 2
If x = 0, we get, y = 0. Putting these values in (1), we get dy/dx = 0, which is not possible as the given value of slope is 3.
And if x =2, we get y = 4.
Therefore, the required point is (2, 4).
Question 7. Find a point on the curve xy + 4 = 0 at which the tangents are inclined at an angle of 45o with the x–axis.
Solution:
Given curve is xy + 4 = 0. We know that the slope of the tangent of a curve is given by dy/dx.
=> x (dy/dx) + y = 0
=> dy/dx = −y/x . . . . (1)
We are given that the tangent is inclined at an angle of 45o with the x–axis. So slope of the tangent is,
dy/dx = tan 45o = 1.
So, (1) becomes,
=> −y/x = 1
=> y = −x
Putting this in the curve xy + 4 = 0 we get,
=> x(−x) + 4 = 0
=> x2 = 4
=> x = ±2
When x = 2, y = −2.
And when x = −2, y = 2.
Therefore, the required points are (2, – 2) & (– 2, 2).
Question 8. Find a point on the curve y = x2 where the slope of the tangent is equal to the x – coordinate of the point.
Solution:
Given curve is y = x2. We know that the slope of the tangent of a curve is given by dy/dx.
=> dy/dx = 2x . . . . (1)
It is given that the slope of the tangent is equal to the x – coordinate of the point.
Therefore, dy/dx = x . . . . (2)
From (1) & (2), we get,
2x = x
=> x = 0
Putting this in the curve y = x2, we get,
=> y = 02
=> y = 0
Therefore, the required point is (0, 0).
Question 9. At what point on the circle x2 + y2 – 2x – 4y + 1 = 0, the tangent is parallel to x – axis.
Solution:
Given circle is x2 + y2 – 2x – 4y + 1 = 0. We know that the slope of the tangent of a curve is given by dy/dx.
=> 2x + 2y (dy/dx) – 2 – 4 (dy/dx) = 0
=> dy/dx = (1– x)/(y– 2)
As the tangent is parallel to x-axis, its slope is equal to 0.
So, (1– x)/(y– 2) = 0
=> x = 1
Putting x = 1 in the circle x2 + y2 – 2x – 4y + 1 = 0, we get,
=> 1 + y2 – 2 – 4y +1 = 0
=> y2 – 4y = 0
=> y (y – 4) = 0
=> y = 0 and y = 4
Therefore, the required points are (1, 0) and (1, 4).
Question 10. At what point of the curve y = x2 does the tangent make an angle of 45o with the x–axis?
Solution:
Given curve is y = x2. We know that the slope of the tangent of a curve is given by dy/dx.
=> dy/dx = 2x . . . . (1)
We are given that the tangent is inclined at an angle of 45o with the x–axis. So slope of the tangent is
Therefore, dy/dx = tan 45o = 1 . . . . (2)
From (1) & (2), we get,
2x = 1
=> x = 1/2
Putting this in the curve y = x2, we get,
=> y = (1/2)2
=> y = 1/4
Therefore, the required point is (1/2, 1/4).
Share your thoughts in the comments
Please Login to comment...