Class 12 RD Sharma Solutions – Chapter 11 Differentiation – Exercise 11.2 | Set 3
Last Updated :
14 Jul, 2021
Question 50. Differentiate y = 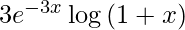 with respect to x.
with respect to x.
Solution:
We have,
y = 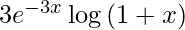
On differentiating y with respect to x we get,
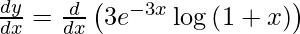
![Rendered by QuickLaTeX.com \frac{d y}{d x} = 3\frac{d}{dx}\left[ e^{- 3x} \log\left( 1 + x \right) \right]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-7e2da0520ec9338f71396f9e1cba7454_l3.png)
On using product rule and chain rule, we get


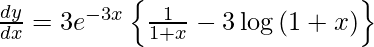
Question 51. Differentiate y = 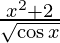 with respect to x.
with respect to x.
Solution:
We have,
y = 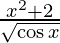
On differentiating y with respect to x we get,
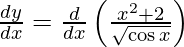
On using quotient rule and chain rule, we get
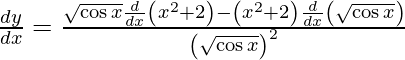

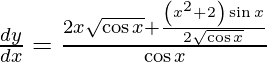
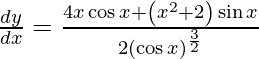
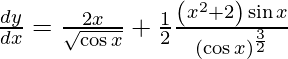
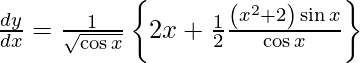
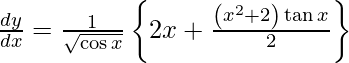
Question 52. Differentiate y = 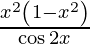 with respect to x.
with respect to x.
Solution:
We have,
y = 
On differentiating y with respect to x we get,

On using quotient rule and chain rule, we get
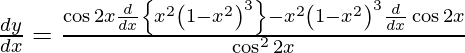
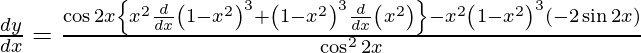
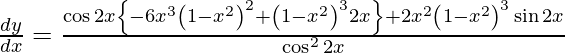

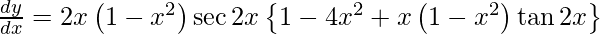
Question 53. Differentiate y = 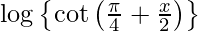 with respect to x.
with respect to x.
Solution:
We have,
y = 
On differentiating y with respect to x we get,
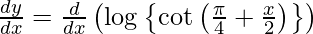
On using chain rule, we get
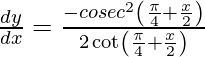

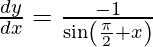
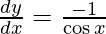

Question 54. Differentiate y = 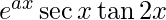 with respect to x.
with respect to x.
Solution:
We have,
y = 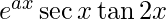
On differentiating y with respect to x we get,
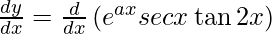
On using chain rule, we get
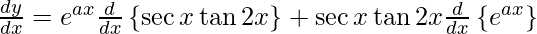
![Rendered by QuickLaTeX.com \frac{d y}{d x} = e^{ax} \left[ \sec x \tan x \tan2x + 2 \sec^2 2x\sec x \right] + a e^{ax} \sec x \tan2x](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-6e964186c3799c5cb3f4ef9bdb76dc5d_l3.png)
![Rendered by QuickLaTeX.com \frac{d y}{d x} = e^{ax} \left[ \sec x \tan x \tan2x + 2 \sec^2 2x\sec x \right] + a e^{ax} sec x \tan2x](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-7e3d491978b87898610d8e0818d33d9f_l3.png)
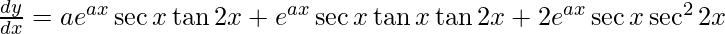
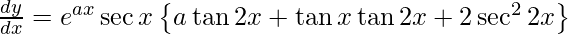
Question 55. Differentiate y = 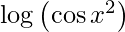 with respect to x.
with respect to x.
Solution:
We have,
y = 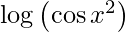
On differentiating y with respect to x we get,
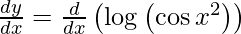
On using chain rule, we get
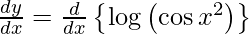
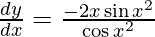
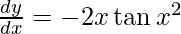
Question 56. Differentiate y =  with respect to x.
with respect to x.
Solution:
We have,
y = 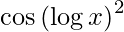
On differentiating y with respect to x we get,
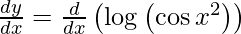
On using chain rule, we get
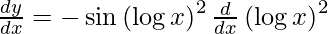

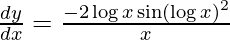
Question 57. Differentiate y = 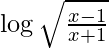 with respect to x.
with respect to x.
Solution:
We have,
y = 
y = 
y = 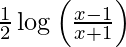
y = ![Rendered by QuickLaTeX.com \frac{1}{2}\left[ \log\left( x - 1 \right) - \log\left( x + 1 \right) \right]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-b582fa2edf9a0354886fc711f9174013_l3.png)
On differentiating y with respect to x we get,
![Rendered by QuickLaTeX.com \frac{d y}{d x} = \frac{d}{dx}\left( \frac{1}{2}\left[ \log\left( x - 1 \right) - \log\left( x + 1 \right) \right] \right)](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-ecfd45a2a9c0e712e496dc114c4a5813_l3.png)
![Rendered by QuickLaTeX.com \frac{d y}{d x} = \frac{1}{2}\left[ \frac{d}{dx}\left\{ \log\left( x - 1 \right) \right\} - \frac{d}{dx}\left\{ \log\left( x + 1 \right) \right\} \right]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-e3e9098e105102a3662038f4debc6096_l3.png)
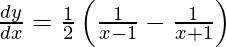
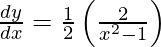
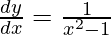
Question 58. If 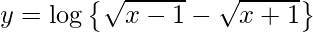 , show that
, show that 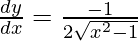 .
.
Solution:
We have,
y = 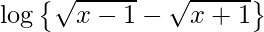
On differentiating y with respect to x we get,

On using chain rule, we get
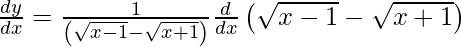
![Rendered by QuickLaTeX.com \frac{d y}{d x} = \frac{1}{\left( \sqrt{x - 1} - \sqrt{x + 1} \right)}\left[ \frac{d}{dx}\sqrt{x - 1} - \frac{d}{dx}\sqrt{x + 1} \right]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-a58797a1c7ae4496216893b41edb1f56_l3.png)
![Rendered by QuickLaTeX.com \frac{d y}{d x} = \frac{1}{\left( \sqrt{x - 1} - \sqrt{x + 1} \right)}\left[ \frac{1}{2} \left( x - 1 \right)^\frac{- 1}{2} - \frac{1}{2} \left( x + 1 \right)^\frac{- 1}{2} \right]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-8cc05678eb8370bfd4550b77a2b87909_l3.png)

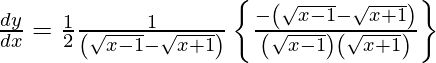
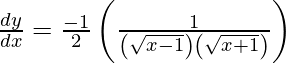
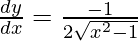
Hence, proved.
Question 59. If y = 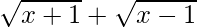 , prove that
, prove that 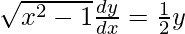 .
.
Solution:
We have,
y = 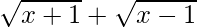
On differentiating y with respect to x we get,



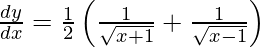
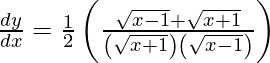

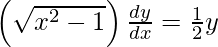
Hence proved.
Question 60. If y = 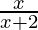 , prove that
, prove that 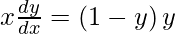 .
.
Solution:
We have,
y = 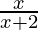
On differentiating y with respect to x we get,
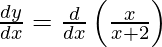
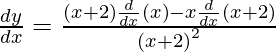

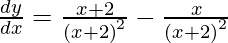
As 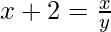 , we have
, we have
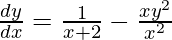
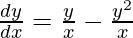
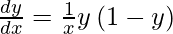
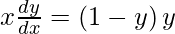
Hence proved.
Question 61. If y = 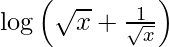 , prove that
, prove that 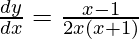 .
.
Solution:
We have,
y = 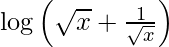
On differentiating y with respect to x we get,

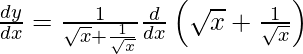

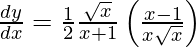
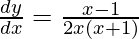
Hence proved.
Question 62. If y = 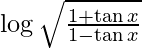 , prove that
, prove that 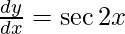 .
.
Solution:
We have,
y = 
y = 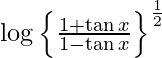
y = 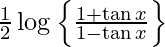
y = 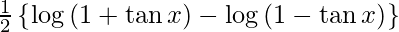
On differentiating y with respect to x we get,
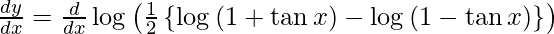
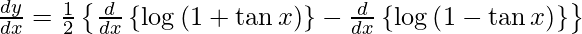
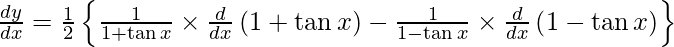
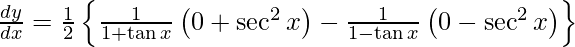

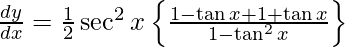
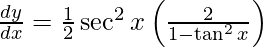
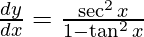
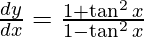
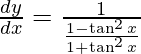
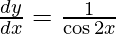
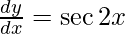
Hence proved.
Question 63. If y = 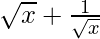 , prove that
, prove that 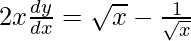 .
.
Solution:
We have,
y = 
On differentiating y with respect to x we get,
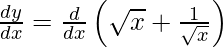

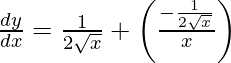

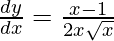
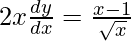
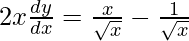
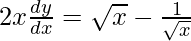
Hence proved.
Question 64. If y = 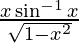 , prove that
, prove that 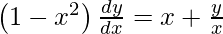 .
.
Solution:
We have,
y = 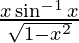
On differentiating y with respect to x we get,
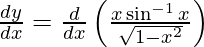
![Rendered by QuickLaTeX.com \frac{d y}{d x} = \left[ \frac{\sqrt{1 - x^2}\frac{d}{dx}\left( x \sin^{- 1} x \right) - \left( x \sin^{- 1} x \right)\frac{d}{dx}\left( \sqrt{1 - x^2} \right)}{\left( \sqrt{1 - x^2} \right)^2} \right]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-6f32b91f9a929c34bb88b29ebb167b42_l3.png)
![Rendered by QuickLaTeX.com \frac{d y}{d x} = \left[ \frac{\sqrt{1 - x^2}\left\{ x\frac{d}{dx}\left( \sin^{- 1} x \right) + \sin^{- 1} x\frac{d}{dx}\left( x \right) \right\} - \left( x \sin^{- 1} x \right)\frac{1}{2\sqrt{1 - x^2}}\frac{d}{dx}\left( 1 - x^2 \right)}{\left( 1 - x^2 \right)} \right]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-eb216757d8ab4d32e10d1cfc1a5f0677_l3.png)
![Rendered by QuickLaTeX.com \frac{d y}{d x} = \left[ \frac{\sqrt{1 - x^2}\left\{ \frac{x}{\sqrt{1 - x^2}} + \sin^{- 1} x \right\} - \frac{x \sin^{- 1} x\left( - 2x \right)}{2\sqrt{1 - x^2}}}{\left( 1 - x^2 \right)} \right]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-4c858b0633ece5da82430c50e40bd32c_l3.png)
![Rendered by QuickLaTeX.com \frac{d y}{d x} = \left[ \frac{x + \sqrt{1 - x^2} \sin^{- 1} x + \frac{x^2 \sin^{- 1} x}{\sqrt{1 - x^2}}}{\left( 1 - x^2 \right)} \right]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-3eb7b7d15800db59516e9c7143e35947_l3.png)
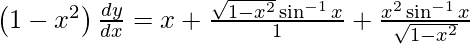
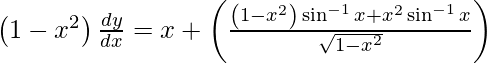
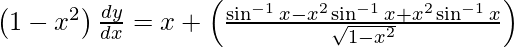
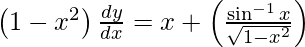
As we have 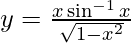 , we get
, we get
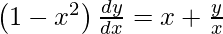
Hence proved.
Question 65. If y = 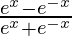 , prove that
, prove that  .
.
Solution:
We have,
y = 
On differentiating y with respect to x we get,

![Rendered by QuickLaTeX.com \frac{d y}{d x} = \left[ \frac{\left( e^x + e^{- x} \right)\frac{d}{dx}\left( e^x - e^{- x} \right) - \left( e^x - e^{- x} \right)\frac{d}{dx}\left( e^x + e^{- x} \right)}{\left( e^x + e^{- x} \right)^2} \right]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-54e970f0ff9f2a509aa13147713af92e_l3.png)
![Rendered by QuickLaTeX.com \frac{d y}{d x} = \left[ \frac{\left( e^x + e^{- x} \right)\left\{ e^x - e^{- x} \frac{d}{dx}\left( - x \right) \right\} - \left( e^x - e^{- x} \right)\left\{ e^x + e^{- x} \frac{d}{dx}\left( - x \right) \right\}}{\left( e^x + e^{- x} \right)^2} \right]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-2e09b6837f3a929c81bb78fbbb229fe7_l3.png)
![Rendered by QuickLaTeX.com \frac{d y}{d x} = \left[ \frac{\left( e^x + e^{- x} \right)\left( e^x + e^{- x} \right) - \left( e^x - e^{- x} \right)\left( e^x - e^{- x} \right)}{\left( e^x + e^{- x} \right)^2} \right]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-a663154a9005ce4fc5c0724941d8c3ac_l3.png)
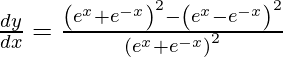
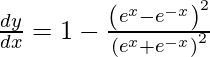
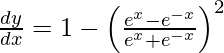
As y = 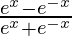 , we have
, we have
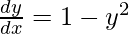
Hence proved.
Question 66. If y = 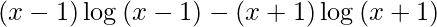 , prove that
, prove that 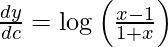 .
.
Solution:
We have,
y = 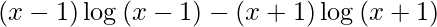
On differentiating y with respect to x we get,
![Rendered by QuickLaTeX.com \frac{d y}{d x} = \frac{d}{dx}\left[ \left( x - 1 \right) \log\left( x - 1 \right) - \left( x + 1 \right) \log\left( x + 1 \right) \right]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-48cce3b5977ab5d0f2b49ac0767b3390_l3.png)
![Rendered by QuickLaTeX.com \frac{d y}{d x} = \left[ \left( x - 1 \right)\frac{d}{dx}\log\left( x - 1 \right) + \log\left( x - 1 \right)\frac{d}{dx}\left( x - 1 \right) \right] - \left[ \left( x + 1 \right)\frac{d}{dx}\log\left( x + 1 \right) + \log\left( x + 1 \right)\frac{d}{dx}\left( x + 1 \right) \right]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-b6b529f3a38196fb786b67d11856daa7_l3.png)
![Rendered by QuickLaTeX.com \frac{d y}{d x} = \left[ \left( x - 1 \right) \times \frac{1}{\left( x - 1 \right)}\frac{d}{dx}\left( x - 1 \right) + \log\left( x - 1 \right) \times \left( 1 \right) \right] - \left[ \left( x + 1 \right) \times \frac{1}{\left( x + 1 \right)} \times \frac{d}{dx}\left( x + 1 \right) + \log\left( x + 1 \right)\left( 1 \right) \right]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-b301d3fe540f3816bf07288eb1c1ac90_l3.png)
![Rendered by QuickLaTeX.com \frac{d y}{d x} = \left[ 1 + \log\left( x - 1 \right) \right] - \left[ 1 + \log\left( x + 1 \right) \right]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-b871bea4fd94080d78455ee37ef62847_l3.png)
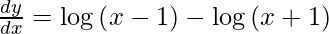
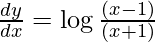
Hence proved.
Question 67. If y = 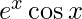 , prove that
, prove that 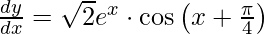 .
.
Solution:
We have,
y = 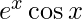
On differentiating y with respect to x we get,
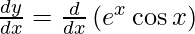

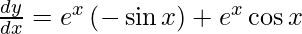
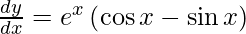
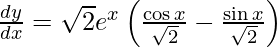

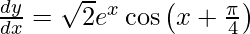
Hence proved.
Question 68. If y = 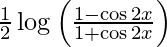 , prove that
, prove that 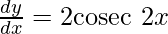 .
.
Solution:
We have,
y = 
y = 
y = 
y = 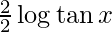
y = 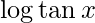
On differentiating y with respect to x we get,
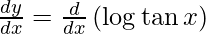
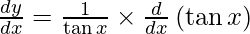
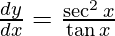
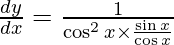
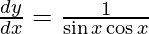
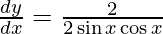
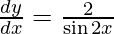
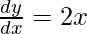
Hence proved.
Question 69. If y = 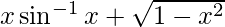 , prove that
, prove that 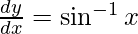 .
.
Solution:
We have,
y = 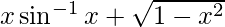
On differentiating y with respect to x we get,
![Rendered by QuickLaTeX.com \frac{d y}{d x} = \frac{d}{dx}\left[ x \sin^{- 1} x + \sqrt{1 - x^2} \right]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-3388411084197113349da525531534b8_l3.png)

![Rendered by QuickLaTeX.com \frac{d y}{d x} = \left[ x \frac{d}{dx} \sin^{- 1} x + \sin^{- 1} x\frac{d}{dx}\left( x \right) \right] + \frac{1}{2\sqrt{1 - x^2}}\frac{d}{dx}\left( 1 - x^2 \right)](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-df4fb6e4a2ad6f386a5e99b83778878b_l3.png)
![Rendered by QuickLaTeX.com \frac{d y}{d x} = \left[ \frac{x}{\sqrt{1 - x^2}} + \sin^{- 1} x \right] - \frac{2x}{2\sqrt{1 - x^2}}](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-065fd83c77e1b55744abf22a06c5c3be_l3.png)
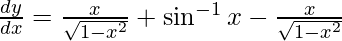
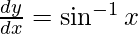
Hence proved.
Question 70. If y = 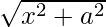 , prove that
, prove that 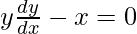 .
.
Solution:
We have,
y = 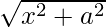
On squaring both sides we get,
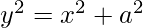
On differentiating both sides with respect to x we get,

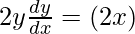
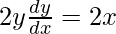

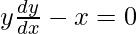
Hence proved.
Question 71. If y = 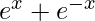 , prove that
, prove that  .
.
Solution:
We have,
y = 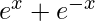
On differentiating both sides with respect to x we get,
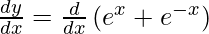
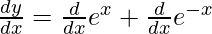
On using chain rule, we get
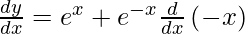
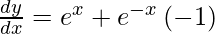
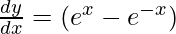
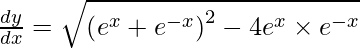
As 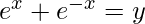 , we get
, we get
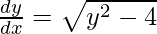
Hence proved.
Question 72. If y = 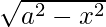 , prove that
, prove that 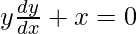 .
.
Solution:
We have,
y = 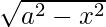
On squaring both sides we get,
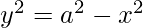
On differentiating both sides with respect to x we get,
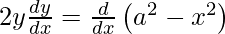
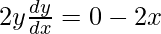

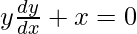
Hence proved.
Question 73. If xy = 4, prove that 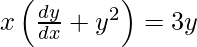 .
.
Solution:
We have,
xy = 4
y = 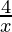
On differentiating both sides with respect to x we get,
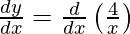

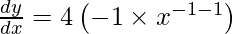
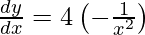
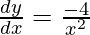
As x = 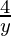 , we get
, we get
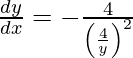
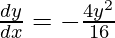
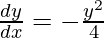
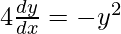
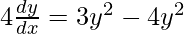


On dividing both sides by x, we get
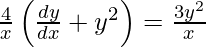
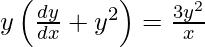

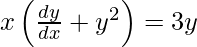
Hence proved.
Question 74. Prove that  .
.
Solution:
We have,
L.H.S. = 
= 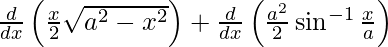
= ![Rendered by QuickLaTeX.com \frac{1}{2}\left[ x\frac{d}{dx}\sqrt{a^2 - x^2} + \sqrt{a^2 - x^2}\frac{d}{dx}\left( x \right) \right] + \frac{a^2}{2} \times \frac{1}{\sqrt{1 - \left( \frac{x}{a} \right)^2}} \times \frac{d}{dx}\left( \frac{x}{a} \right)](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-c335be31f61518244dcb473a23b9e152_l3.png)
= ![Rendered by QuickLaTeX.com \frac{1}{2}\left[ x \times \frac{1}{2\sqrt{a^2 - x^2}}\frac{d}{dx}\left( a^2 - x^2 \right) + \sqrt{a^2 - x^2} \right] + \left[ \frac{a^2}{2} \right] \times \frac{1}{\sqrt{\frac{a^2 - x^2}{a^2}}} \times \left( \frac{1}{a} \right)](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-5856c08c8e324f894e9a94b0b006b62d_l3.png)
= ![Rendered by QuickLaTeX.com \frac{1}{2}\left[ \frac{x\left( - 2x \right)}{2\sqrt{a^2 - x^2}} + \sqrt{a^2 - x^2} \right] + \left( \frac{a^2}{2} \right)\frac{a}{\sqrt{a^2 - x^2}} \times \left( \frac{1}{a} \right)](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-5bd92f7a4d6aa798fe9da49ee4ae1329_l3.png)
= ![Rendered by QuickLaTeX.com \frac{1}{2}\left[ \frac{- 2 x^2 + 2\left( a^2 - x^2 \right)}{2\sqrt{a^2 - x^2}} \right] + \frac{a^2}{2\sqrt{a^2 - x^2}}](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-fbab0e00ee2b5000dcaa336fdd3c217f_l3.png)
= ![Rendered by QuickLaTeX.com \frac{1}{2}\left[ \frac{2\left( a^2 - 2 x^2 \right)}{2\sqrt{a^2 - x^2}} \right] + \frac{a^2}{2\sqrt{a^2 - x^2}}](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-7360ec3b3f5b8edac3c3ed1462fbc812_l3.png)
= 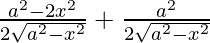
= 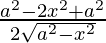
= 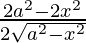
= 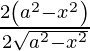
= 
= 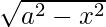
= R.H.S.
Hence proved.
Share your thoughts in the comments
Please Login to comment...