Class 12 RD Sharma Solutions – Chapter 11 Differentiation – Exercise 11.2 | Set 1
Last Updated :
14 Jul, 2021
Question 1. Differentiate y = sin (3x + 5) with respect to x.
Solution:
We have,
y = sin (3x + 5)
On differentiating y with respect to x we get,
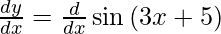
On using chain rule, we have
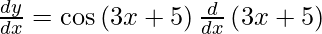
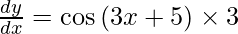
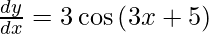
Question 2. Differentiate y = tan2 x with respect to x.
Solution:
We have,
y = tan2 x
On differentiating y with respect to x we get,
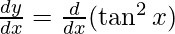
On using chain rule, we have
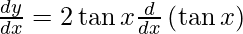
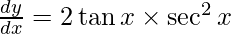
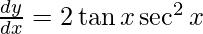
Question 3. Differentiate y = tan (x + 45°) with respect to x.
Solution:
We have,
y = tan (x + 45°)
y = 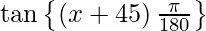
On differentiating y with respect to x we get,
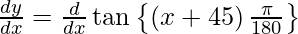
On using chain rule, we have
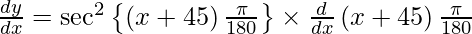
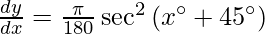
Question 4. Differentiate y = sin (log x) with respect to x.
Solution:
We have,
y = sin (log x)
On differentiating y with respect to x we get,
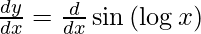
On using chain rule, we have
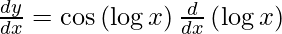
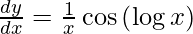
Question 5. Differentiate y = esin √x with respect to x.
Solution:
We have,
y = esin √x
On differentiating y with respect to x we get,
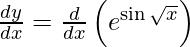
On using chain rule, we have
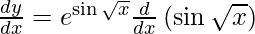
On using chain rule again, we have
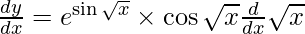
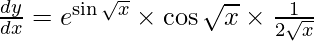
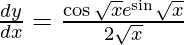
Question 6. Differentiate y = etan x with respect to x.
Solution:
We have,
y = etan x
On differentiating y with respect to x we get,
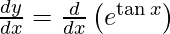
On using chain rule, we have
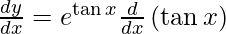
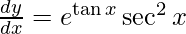
Question 7. Differentiate y = sin2 (2x + 1) with respect to x.
Solution:
We have,
y = sin2 (2x + 1)
On differentiating y with respect to x we get,
![Rendered by QuickLaTeX.com \frac{d y}{d x} = \frac{d}{dx}\left[ \sin^2 \left( 2x + 1 \right) \right]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-e1fd5fcadd4e9e4c9d4a67f245b98023_l3.png)
On using chain rule, we have
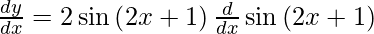
On using chain rule again, we have
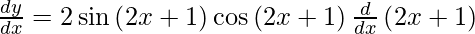
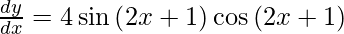
As sin 2A = 2 sin A cos A, we get
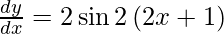
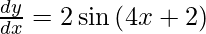
Question 8. Differentiate y = log7 (2x − 3) with respect to x.
Solution:
We have,
y = log7 (2x − 3)
As 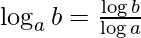 , we have
, we have
y = 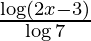
On differentiating y with respect to x we get,
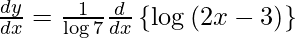
On using chain rule, we have
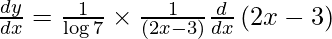
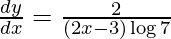
Question 9. Differentiate y = tan 5x° with respect to x.
Solution:
We have,
y = tan 5x°
y = 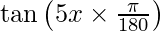
On differentiating y with respect to x we get,
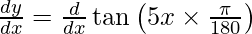
On using chain rule, we have
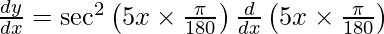
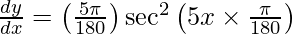
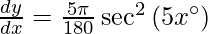
Question 10. Differentiate y = 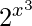 with respect to x.
with respect to x.
Solution:
We have,
y = 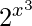
On differentiating y with respect to x we get,
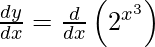
On using chain rule, we have
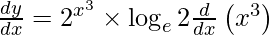
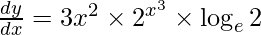
Question 11. Differentiate y = 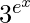 with respect to x.
with respect to x.
Solution:
We have,
y = 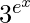
On differentiating y with respect to x we get,
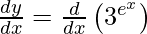
On using chain rule, we have
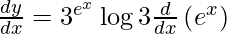
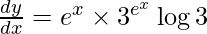
Question 12. Differentiate y = logx 3 with respect to x.
Solution:
We have,
y = logx 3
As 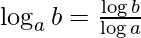 , we get
, we get
y = 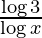
On differentiating y with respect to x we get,
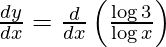
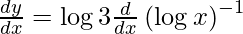
On using chain rule, we have
![Rendered by QuickLaTeX.com \frac{d y}{d x} = \log3 \times \left[ - 1 \left( \log x \right)^{- 2} \right]\frac{d}{dx}\left( \log x \right)](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-917f6a51659aa984b0108509f45f7e8a_l3.png)
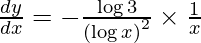
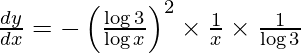
As 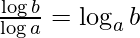 , we get
, we get
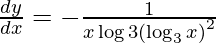
Question 13. Differentiate y = 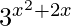 with respect to x.
with respect to x.
Solution:
We have,
y = 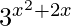
On differentiating y with respect to x we get,
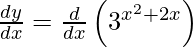
On using chain rule, we have
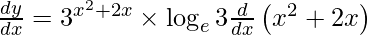
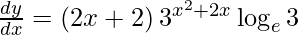
Question 14. Differentiate y = 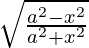 with respect to x.
with respect to x.
Solution:
We have,
y = 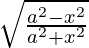
On differentiating y with respect to x we get,
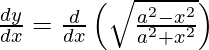
On using chain rule, we have
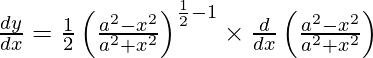
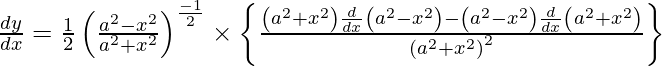

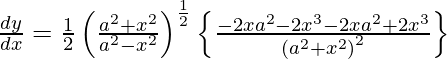
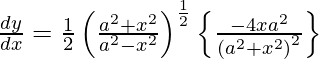
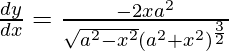
Question 15. Differentiate y = 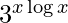 with respect to x.
with respect to x.
Solution:
We have,
y = 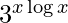
On differentiating y with respect to x we get,
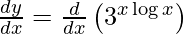
On using chain rule, we have
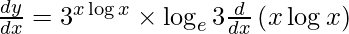
![Rendered by QuickLaTeX.com \frac{d y}{d x} = 3^x \log x \times \log_e 3\left[ x\frac{d}{dx}\left( \log x \right) + \log x\frac{d}{dx}\left( x \right) \right]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-e57ca2fbb7d7a737925aa5957a5b7a02_l3.png)
![Rendered by QuickLaTeX.com \frac{d y}{d x} = 3^{x \log x} \times \log_e 3\left[ \frac{x}{x} + \log x \right]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-b37340b339fbd348fc37c3ba9a13f770_l3.png)
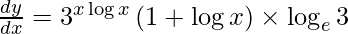
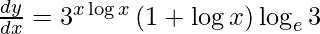
Question 16. Differentiate y = 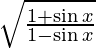 with respect to x.
with respect to x.
Solution:
We have,
y = 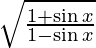
On differentiating y with respect to x we get,
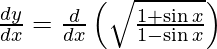
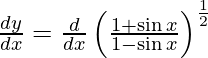
On using chain rule, we have
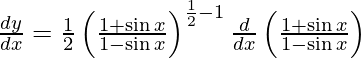
![Rendered by QuickLaTeX.com \frac{d y}{d x} = \frac{1}{2} \left( \frac{1 - \sin x}{1 + \sin x} \right)^\frac{1}{2} \left[ \frac{\left( 1 - \sin x \right)\left( \cos x \right) - \left( 1 + \sin x \right)\left( - \cos x \right)}{\left( 1 - \sin x \right)^2} \right]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-d0af64861031fc2e10422b97e18b2666_l3.png)
![Rendered by QuickLaTeX.com \frac{d y}{d x} = \frac{1}{2}\frac{\left( 1 - \sin x \right)^\frac{1}{2}}{\left( 1 + \sin x \right)^\frac{1}{2}}\left[ \frac{\cos x - \cos x \sin x + \cos x + \sin x \cos x}{\left( 1 - \sin x \right)^2} \right]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-6218bdc45f7de235481ff679392a16a7_l3.png)
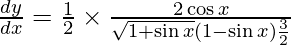
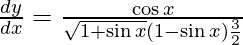
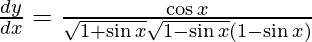
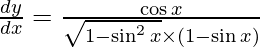
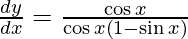
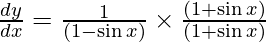
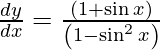
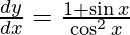
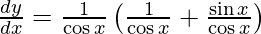
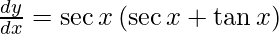
Question 17. Differentiate y = 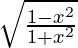 with respect to x.
with respect to x.
Solution:
We have,
y = 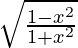
On differentiating y with respect to x we get,
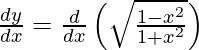
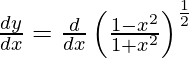
On using chain rule, we have
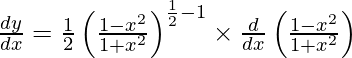
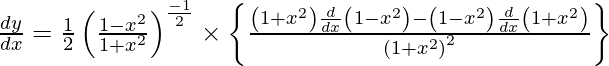
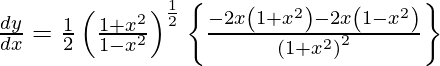
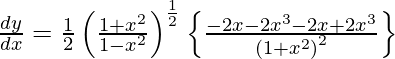
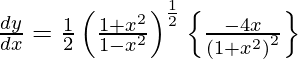
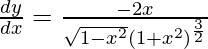
Question 18. Differentiate y = (log sin x)2 with respect to x.
Solution:
We have,
y = (log sin x)2
On differentiating y with respect to x we get,
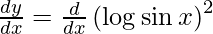
On using chain rule, we have
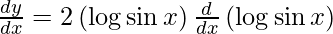
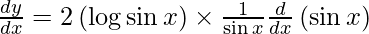
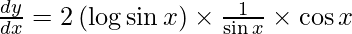
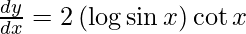
Question 19. Differentiate y = 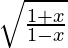 with respect to x.
with respect to x.
Solution:
We have,
y = 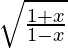
On differentiating y with respect to x we get,
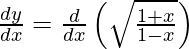
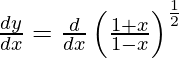
On using chain rule, we have
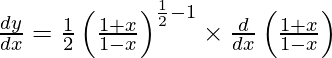
On using quotient rule, we have

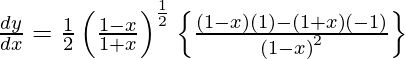
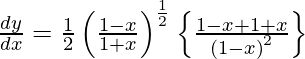
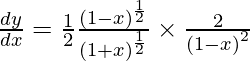
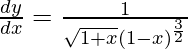
Question 20. Differentiate y = 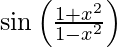 with respect to x.
with respect to x.
Solution:
We have,
y = 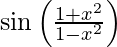
On differentiating y with respect to x we get,
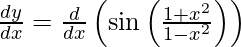
On using chain rule, we have
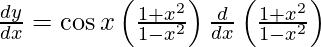
On using quotient rule, we have
![Rendered by QuickLaTeX.com \frac{d y}{d x} = \cos x\left( \frac{1 + x^2}{1 - x^2} \right)\left[ \frac{\left( 1 - x^2 \right)\frac{d}{dx}\left( 1 + x^2 \right) - \left( 1 + x^2 \right)\frac{d}{dx}\left( 1 - x^2 \right)}{\left( 1 - x^2 \right)^2} \right]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-bddedfb63b1c94b8675018ba115fda60_l3.png)
![Rendered by QuickLaTeX.com \frac{d y}{d x} = \cos x\left( \frac{1 + x^2}{1 - x^2} \right)\left[ \frac{\left( 1 - x^2 \right)\left( 2x \right) - \left( 1 + x^2 \right)\left( - 2x \right)}{\left( 1 - x^2 \right)^2} \right]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-b95a0dbad805cafbcbe2b162be7ef69e_l3.png)
![Rendered by QuickLaTeX.com \frac{d y}{d x} = \cos x\left( \frac{1 + x^2}{1 - x^2} \right)\left[ \frac{2x - 2 x^3 + 2x + 2 x^3}{\left( 1 - x^2 \right)^2} \right]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-7764792af93cf5266173cdf0b73a4deb_l3.png)
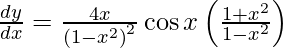
Question 21. Differentiate y = 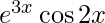 with respect to x.
with respect to x.
Solution:
We have,
y = 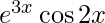
On differentiating y with respect to x we get,
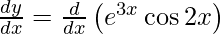
On using product rule, we have
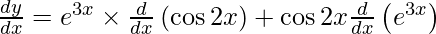
On using chain rule, we have
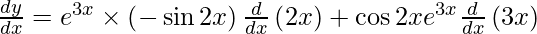
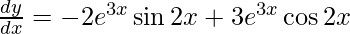
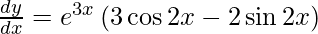
Question 22. Differentiate y = sin(log sin x) with respect to x.
Solution:
We have,
y = sin(log sin x)
On differentiating y with respect to x we get,
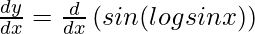
On using chain rule, we have
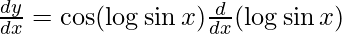
On using chain rule again, we have
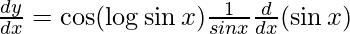
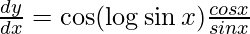
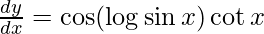
Question 23. Differentiate y = etan 3x with respect to x.
Solution:
We have,
y = etan 3x
On differentiating y with respect to x we get,
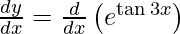
On using chain rule, we have
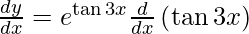
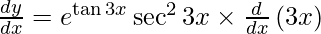
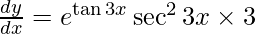
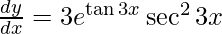
Question 24. Differentiate y = 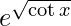 with respect to x.
with respect to x.
Solution:
We have,
y = 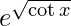
On differentiating y with respect to x we get,
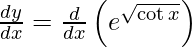
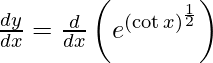
On using chain rule, we have
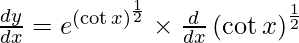
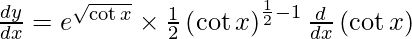
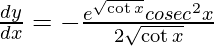
Share your thoughts in the comments
Please Login to comment...