Question 10. If f, g, h are three functions defined from R to R as follows:
(i) f(x) = x2
(ii) g(x) = sinx
(iii) h(x) = x2 + 1
Find the range of each function.
Solution:
(i) We have,
f(x) = x2
Range of f(x) = R+ (set of all real numbers greater than or equal to zero)
= {x ∈ R+ | x ≥ 0}
(ii) We have
g(x) = sinx
Range of g(x) = {x ∈ R : -1 ≤ x ≤ 1}
(iii) We have
h(x) = x2 + 1
Range of h(x) = {x ∈ R : x ≥ 1}
Question 11. Let X = {1, 2, 3, 4} and Y = {1, 5, 9, 11, 15, 16}
Determine which of the following sets are functions from X to Y
(a) f1 = {(1, 1), (2, 11), (3, 1), (4, 15)}
(b) f = {(1, 1), (2, 7), (3, 5)}
(c) f = {(1,5), (2, 9), (3, 1), (4, 5), (2, 11)}
Solution:
(a) We have,
f1 = {(1, 1), (2, 11), (3, 1), (4, 15)}
f1 is a function from X to Y
(b) We have,
f2 = {(1, 1), (2, 7), (3, 5)}
f2 is not a function from X to Y because there is an element 4 ∈ x which is not associated to any element of Y.
(c) We have,
f3 = {(1, 5), (2, 9), (3, 1), (4, 5), (2, 11)}
f3 is not a function from X to Y because an element 2 ∈ x is associated to two elements 9 and 11 in Y.
Question 12. Let A = {12, 13, 14, 15, 16, 17} and f : A ⇢ Z be a function given by f(x) = highest prime factor of x. Find range of f.
Solution:
We have,
f(x) = highest prime factor of x.
Therefore,
12 = 3 × 4,
13 = 13 × 1,
14 = 7 × 2,
15 = 5 × 3,
16 = 2 × 8,
17 = 17 × 1
Therefore,
f = {(12, 3), (13, 3), (14, 7), (15, 5), (16, 2), (17, 17)}
Range (f) = {3, 13, 7, 5, 2, 17}
Question 13. If f : R ⇢ R be defined by f(x) = x2 + 1, then find f-1{17} and f-1{-3}.
Solution:
We know that,
if f : A ⇢ 13
such that y ∈ 3. Then,
f-1 (y) = {x ∈ A : f(x) = y}. In other words, f-1 (y) is the set of pre-images of y.
Let f-1 (17) = x. Then, f(x) = 17
⇒ x2 + 1 = 17
⇒ x2 = 17 – 1 = 16
⇒ x = ±4
Let f-1 {-3} = x. Then, f(x) = -3
⇒ x2 + 1 = -3
⇒ x2 = -3 – 1 = -4
⇒ x = 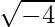
Therefore, f-1 {-3} = 0
Question 14. Let A = {p, q, r, s} and B = {1, 2, 3}. Which of the following relations form A to B is not a function?
(a) R1 = R1 = {(p, 1), (q, 2), (r, 1), (s, 2)}
(b) R2 = {(p, 1), (q, 1), (r, 1), (s, 2)}
(c) R3 = {(p, 1), (q, 2), (p, 2), (s, 3)}
(d) R4 = {(p, 2), (q, 3), (r, 2), (s, 2)}
Solution:
We have
A = {p, q, r, s} and B = {1, 2, 3}
(a) Now,
R1 = {(p, 1), (q, 2), (r, 1), (s, 2)}
R1 is a function
(b) Now,
R2 = {(p, 1), (q, 2), (r, 1), (s, 1)}
R2 is a function
(c) Now,
R3 = {(p, 2), (q, 3), (r, 2), (s, 2)}
R3 is not a function because an element p ∈ A is associated to two elements 1 and 2 in B.
(d) Now,
R4 = {(p, 2), (q, 3), (r, 2), (s, 2)}
R4 is a function
Question 15. Let A = {9, 10, 11, 12, 13} and let f : A ⇢ N be defined by f(n) = the highest prime factor of n. Find the range of f.
Solution:
We have,
f(n) = the highest prime factor of n.
Now,
9 = 3 × 3,
10 = 5 × 2,
11 = 11 × 1,
12 = 3 × 4,
13 = 13 × 1
Therefore,
f = {(9, 3), (10, 5), (11, 11), (12, 3), (13, 13)}
Clearly, range(f) = {3, 5, 11, 13}
Question 16. The function f is defined by
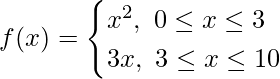
The relation f is defined by
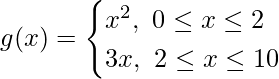
Show that f is a function and g is not a function
Solution:
We have,
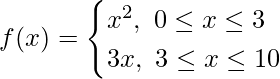
and,
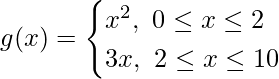
Now, f(3) = (3)2 = 9 and f(3) = 3 × 3 = 9
and, g(2) = (2)2 = 4 and g(2) = 3 × 2 = 6
We observe that f(x) takes unique value at each point in its domain [0,10]. However, g(x) does not take unique value at each point in its domain [0, 10].
Hence, g(x) is not a function.
Question 17. If f(x) = x2, find
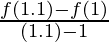
Solution:
Given f(x) = x2
f(1.1) = 1.21
f(1) = 1
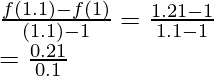
= 2.1
Question 18. Express the function f : X ⇢ R given by f(x) = x3 + 1 as set of ordered pairs, where x = {-1, 0, 3, 9, 7}.
Solution:
f : X ⇢ R given by f(x) = x3 + 1
f(-1) = (-1)3 + 1 = -1 + 1 = 0
f(0) = (0)3 + 1 = 0 + 1 = 1
f(3) = (3)3 + 1 = 27 + 1 = 28
f(9) = (9)3 + 1 = 81 + 1 = 82
f(7) = (7)3 + 1 = 343 + 1 = 344
Set of ordered pairs are {(-1, 0), (0, 1), (3, 28), (9, 82), (7, 344)}
Share your thoughts in the comments
Please Login to comment...